標籤：並查集

題目

題目傳送門

題目描述

現有一塊大乳酪，它的高度為 $h$，它的長度和寬度我們可以認為是無限大的，乳酪 中間有許多 半徑相同 的球形空洞。我們可以在這塊乳酪中建立空間座標系，在座標系中， 乳酪的下表面為$z = 0$，乳酪的上表面為$z = h$。

現在，乳酪的下表面有一隻小老鼠 Jerry，它知道乳酪中所有空洞的球心所在的坐 標。如果兩個空洞相切或是相交，則 Jerry 可以從其中一個空洞跑到另一個空洞，特別 地，如果一個空洞與下表面相切或是相交，Jerry 則可以從乳酪下表面跑進空洞；如果 一個空洞與上表面相切或是相交，Jerry 則可以從空洞跑到乳酪上表面。

位於乳酪下表面的 Jerry 想知道，在 不破壞乳酪 的情況下，能否利用已有的空洞跑 到乳酪的上表面去?

空間內兩點$P_1(x_1,y_1,z_1)$、$P2(x_2,y_2,z_2)$的距離公式如下：

$\mathrm{dist}(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

輸入輸出格式

輸入格式

每個輸入檔案包含多組資料。

的第一行，包含一個正整數 $T$，代表該輸入檔案中所含的資料組數。

接下來是 $T$ 組資料，每組資料的格式如下： 第一行包含三個正整數 $n,h$ 和 $r$，兩個數之間以一個空格分開，分別代表乳酪中空 洞的數量，乳酪的高度和空洞的半徑。

接下來的 $n$ 行，每行包含三個整數 $x,y,z$，兩個數之間以一個空格分開，表示空 洞球心座標為$(x,y,z)$。

輸出格式

$T$ 行，分別對應 $T$ 組資料的答案，如果在第 $i$ 組資料中，Jerry 能從下 表面跑到上表面，則輸出Yes，如果不能，則輸出No （均不包含引號）。

輸入輸出樣例

輸入樣例#1

3 
2 4 1 
0 0 1 
0 0 3 
2 5 1 
0 0 1 
0 0 4 
2 5 2 
0 0 2 
2 0 4
 

輸出樣例#1

Yes
No
Yes

說明

【輸入輸出樣例 1 說明】

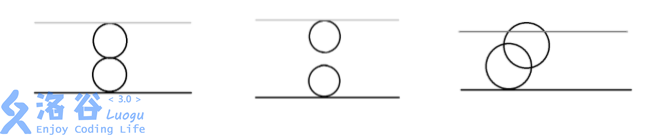
第一組資料,由乳酪的剖面圖可見：

第一個空洞在$(0,0,0)$與下表面相切

第二個空洞在$(0,0,4)$與上表面相切 兩個空洞在$(0,0,2)$相切

輸出 Yes

第二組資料,由乳酪的剖面圖可見：

兩個空洞既不相交也不相切

輸出 No

第三組資料,由乳酪的剖面圖可見：

兩個空洞相交 且與上下表面相切或相交

輸出 Yes

【資料規模與約定】

對於 $20\%$的資料,$n = 1$,$1 \le h$ , $r \le 10,000$,座標的絕對值不超過 $10,000$。

對於 $40\%$的資料,$1 \le n \le 8$, $1 \le h$ , $r \le 10,000$,座標的絕對值不超過 $10,000$。

對於$80\%$的資料, $1 \le n \le 1,000$, $1 \le h , r \le 10,000$,座標的絕對值不超過$10,000$。

對於 $100\%$的資料,$1 \le n \le 1,000$,$1 \le h , r \le 1,000,000,000$,$T \le 20$,座標的 絕對值不超過 $1,000,000,000$。

題解

建圖之後傳遞閉包

或者並查集（應該比我的程式碼要快）

code

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dep(i,a,b) for(int i=a;i>=b;i--)
#define ll long long
#define mem(x,num) memset(x,num,sizeof x)
using namespace std;
inline ll read(){
    ll f=1,x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int maxn=2e3+6,inf=0x3f3f3f;
ll cnt=0,T,n,r,h,x[maxn],y[maxn],z[maxn],dis[maxn],Map[maxn][maxn];
int que[maxn],inque[maxn];

void spfa(){
    int head=0,tail=1;
    que[head]=0,inque[0]=1,dis[0]=1;
    while(head<tail){
        int now=que[head];
        rep(j,0,n+1)
            if(Map[now][j]==1&&dis[now]==1&&dis[j]==0){
                dis[j]=1;
                if(!inque[j])inque[j]=1,que[tail++]=j;
            }
        inque[now]=0;head++;
    }
}
int main(){
    T=read();
    while(T--){
        mem(x,0);mem(y,0);mem(z,0);mem(Map,0);mem(inque,0);mem(dis,0);
        n=read(),h=read(),r=read();
        rep(i,1,n)x[i]=read(),y[i]=read(),z[i]=read();
        rep(i,1,n)
            rep(j,1,n){
                if(i==j)continue;
                double t=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])+(z[i]-z[j])*(z[i]-z[j]));
                if(t<=2*r)Map[i][j]=Map[j][i]=1;
            }
        rep(i,1,n)if(z[i]-r<=0)Map[0][i]=Map[i][0]=1;
        rep(i,1,n)if(z[i]+r>=h)Map[i][n+1]=Map[n+1][i]=1;
        spfa();
        if(dis[n+1]==1)printf("Yes\n");else printf("No\n");
    }
    return 0;
}