Deep Residual Learning for Image Recognition

原文連結

摘要

深度神經網路很難去訓練，本文提出了一個殘差學習框架來簡化那些非常深的網路的訓練，該框架使得層能根據其輸入來學習殘差函式而非原始函式。本文提出證據表明，這些殘差網路的優化更簡單，而且通過增加深度來獲得更高的準確率

引言

深度網路很好的將一個端到端的多層模型中的低/中/高階特徵以及分類器整合起來，特徵的等級可以通過所堆疊層的數量來豐富。有結果顯示，模型的深度發揮著至關重要的作用

在深度的重要性的驅使下，出現了一個新的問題：訓練一個更好的網路是否和堆疊更多的層一樣簡單呢？解決這一問題的障礙便是困擾人們很久的梯度消失/梯度爆炸，這從一開始便阻礙了模型的收斂。歸一初始化（normalized initialization）和中間歸一化（intermediate normalization）在很大程度上解決了這一問題，它使得數十層的網路在反向傳播的隨機梯度下降（SGD）上能夠收斂。當深層網路能夠收斂時，一個退化問題又出現了：隨著網路深度的增加，準確率達到飽和（不足為奇）然後迅速退化。意外的是，這種退化並不是由過擬合造成的，並且在一個合理的深度模型中增加更多的層卻導致了更高的錯誤率

深層"plain"網路的在CIFAR-10上的錯誤率

退化的出現（訓練準確率）表明了並非所有的系統都是很容易優化的。本文提出了一種深度殘差學習框架來解決這個退化問題。方法是讓這些層來擬合殘差對映，而不是讓每一個堆疊的層直接來擬合所需的底層對映。假設所需的底層對映為\(H(x)\)，讓堆疊的非線性層來擬合另一個對映：\(F(x):=H(x)−x\)。 因此原來的對映轉化為：\(F(x)+x\)，研究者推斷殘差對映比原始未參考的對映（unreferenced mapping）更容易優化，在極端的情況下，如果某個恆等對映是最優的，那麼將殘差變為0比用非線性層的堆疊來擬合恆等對映更簡單

公式 F(x)+x 可以通過前饋神經網路的“shortcut連線”

來實現，Shortcut連線就是跳過一個或者多個層。shortcut 連線只是簡單的執行恆等對映，再將它們的輸出和堆疊層的輸出疊加在一起。恆等的shortcut連線並不增加額外的引數和計算複雜度。完整的網路仍然能通過端到端的SGD反向傳播進行訓練，並且能夠簡單的通過公共庫（例如，Caffe）來實現而無需修改求解器

一個殘差網路構建塊(Fig.2)

本文表明

1. 極深的殘差網路是很容易優化的，但是對應的“plain”網路（僅是堆疊了層）在深度增加時卻出現了更高的錯誤率
   
2. 深度殘差網路能夠輕易的由增加層來提高準確率，並且結果也大大優於以前的網路

深度殘差學習

殘差學習

將\(H(x)\)

看作一個由部分堆疊的層來擬合的底層對映，其中\(x\)是這些層的輸入。假設多個非線性層能夠逼近複雜的函式，這就等價於這些層能夠逼近複雜的殘差函式，例如，\(H(x) - x\)。我們明確地讓這些層來估計一個殘差函式：\(F(x):=H(x)−x\)而不是\(H(x)\)。因此原始函式變成了：\(F(x)+x\)。儘管這兩個形式應該都能夠逼近所需的函式，但是前者更易學習。使用這種表達方式的原因是之前提到的退化問題，使用殘差學習的方式重新表達後，如果恆等對映是最優的，那麼求解器將驅使多個非線性層的權重趨向於零來逼近恆等對映。如果最優函式更趨近於恆等對映而不是0對映，那麼對於求解器來說尋找關於恆等對映的擾動比學習一個新的函式要容易的多，實驗表明，學習到的殘差函式通常只有很小的響應，說明了恆等對映提供了合理的預處理

通過捷徑進行identity mapping

在堆疊層上採取殘差學習演算法，一個構件塊如上圖(Fig.2)所示，其定義為(Eq.1)
\[ y = F(x, {W_i}) + x \]
其中\(x\)和\(y\)分別表示層的輸入和輸出。函式\(F(x, {Wi})\)代表著學到的殘差對映，該shortcut連線沒有增加額外的引數和計算複雜度

在Eq.1中，\(x\)和\(F\)的維度必須相同，如果不同，可以通過shortcut連線執行一個線性對映\(W_s\) 來匹配兩者的維度(Eq.2)
\[ y = F({x, {W_i}}) + W_sx \]
實驗表明，恆等對映已足夠解決退化問題，並且是經濟的，因此\(W_s\)只是用來解決維度不匹配的問題

不僅是對於全連線層，對於卷積層殘差連線也是同樣適用的。函式\(F(x, {W_i})\)可以表示多個卷積層，在兩個特徵圖的通道之間執行元素級的加法

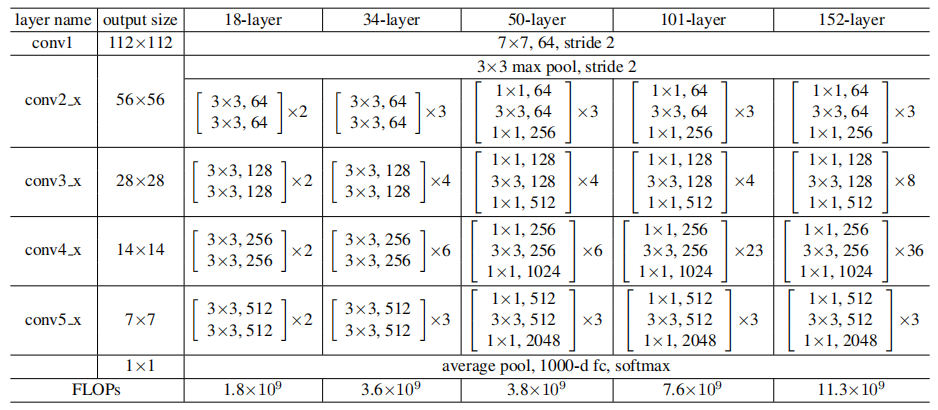
網路架構

VGG、普通網路與殘差網路的配置對比

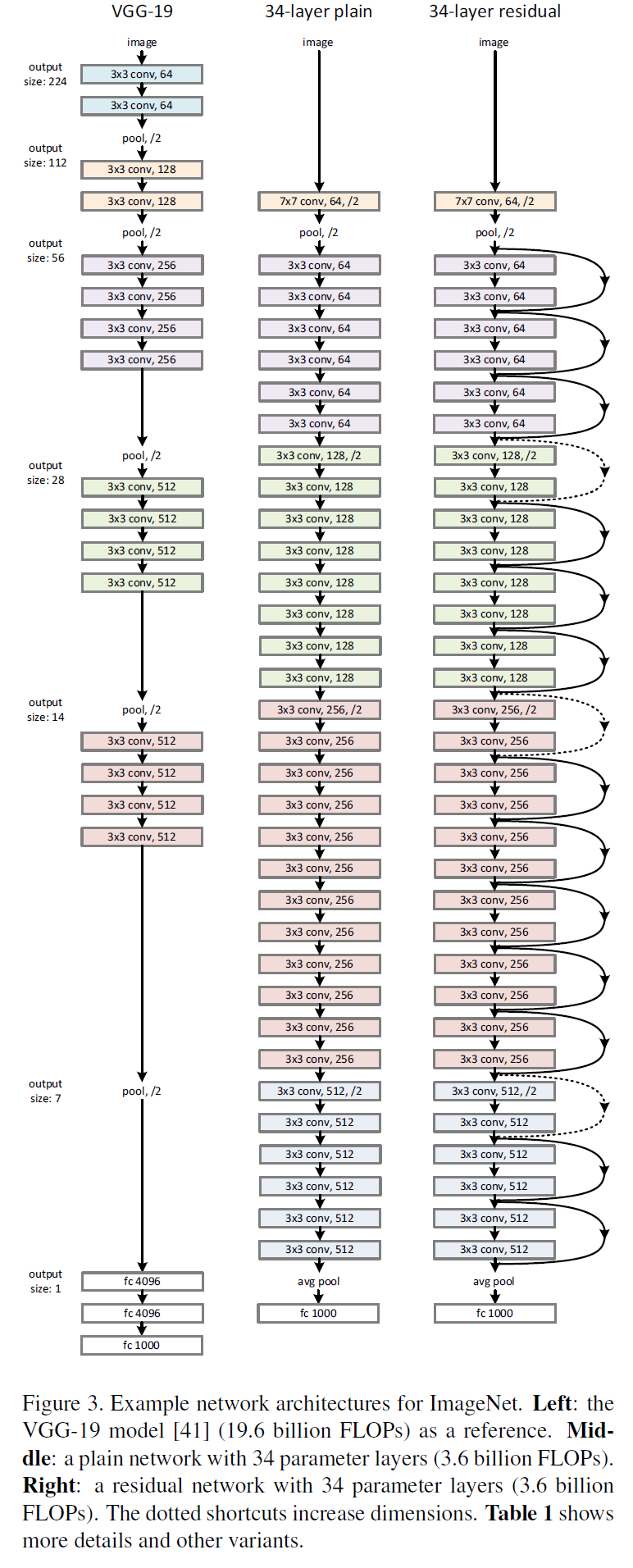
詳細架構

普通網路

卷積層主要為3*3的濾波器，並遵循以下兩點要求

1. 輸出特徵尺寸相同的層含有相同數量的濾波器
   
2. 如果特徵尺寸減半，則濾波器的數量增加一倍來保證每層的時間複雜度相同

直接通過stride為2的卷積層來進行下采樣。在網路的最後是一個全域性的平均pooling層和一個1000 類的包含softmax的全連線層。加權層的層數為34

殘差網路

在普通網路的基礎上，插入shortcut連線，將網路變成了對應的殘差版本。如果輸入和輸出的維度相同時，可以直接使用恆等shortcuts(Eq.1)(殘差連線實線部分)，當維度增加時(殘差連線虛線部分)，考慮兩個選項

1. shortcut仍然使用恆等對映，在增加的維度上使用0來填充，這樣做不會增加額外的引數
   
2. 使用Eq.2的對映shortcut來使維度保持一致（通過1*1的卷積）

對於這兩個選項，當shortcut跨越兩種尺寸的特徵圖時，均使用stride為2的卷積

實驗

普通網路
實驗表明34層的網路比18層的網路具有更高的驗證錯誤率，比較了訓練過程中的訓練及驗證錯誤率之後，觀測到了明顯的退化現象----在整個訓練過程中34 層的網路具有更高的訓練錯誤率，即使18層網路的解空間為34層解空間的一個子空間

殘差網路
實驗觀察到以下三點

1. 34層的ResNet比18層ResNet的結果更優。更重要的是，34 層的ResNet在訓練集和驗證集上均展現出了更低的錯誤率。這表明了這種設定可以很好的解決退化問題，並且可以由增加的深度來提高準確率
   
2. 與對應的普通網路相比，34層的ResNet在top-1 錯誤率上降低了3.5%，這得益於訓練錯誤率的降低，也驗證了在極深的網路中殘差學習的有效性
   
3. 18層的普通網路和殘差網路的準確率很接近，但是ResNet 的收斂速度要快得多

錯誤率比較

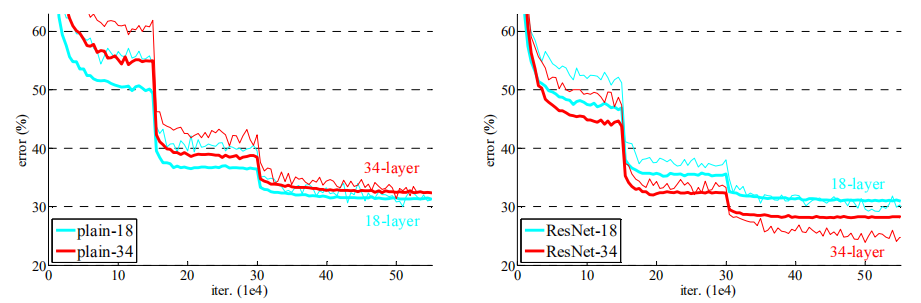
如果網路"並不是特別深"(如18層)，現有的SGD能夠很好的對普通網路進行求解，而ResNet能夠使優化得到更快的收斂

恆等 vs 對映 Shortcuts

已經驗證了無引數的恆等shortcuts是有助於訓練的。接下來研究對映shortcut(Eq.2)，比較了三種選項

1. 對增加的維度使用0填充，所有的shortcuts是無引數的
   
2. 對增加的維度使用對映shortcuts，其它使用恆等shortcuts
   
3. 所有的都是對映shortcuts

實驗表明三種選項的模型都比普通模型要好，2略好於1，研究者認為這是因為1中的0填充並沒有進行殘差學習。3略好於2，研究者將其歸結於更多的（13個）對映shortcuts所引入的引數，實驗結果也表明對映shortcuts對於解決退化問題並不是必需的，因此為了減少複雜度和模型尺寸，在之下的研究中並不使用模型3。恆等shortcuts因其無額外複雜度而對以下介紹的瓶頸結構尤為重要

深度瓶頸結構

將構建塊修改為瓶頸設計。對於每一個殘差函式\(F\)，使用了三個疊加層而不是兩個，這三層分別是1*1、3*3 和1*1 的卷積，1*1 的層主要負責減少然後增加（恢復）維度，剩下的3*3的層來減少輸入和輸出的維度

構建塊(Fig.5)，這兩種設計具有相似的時間複雜度

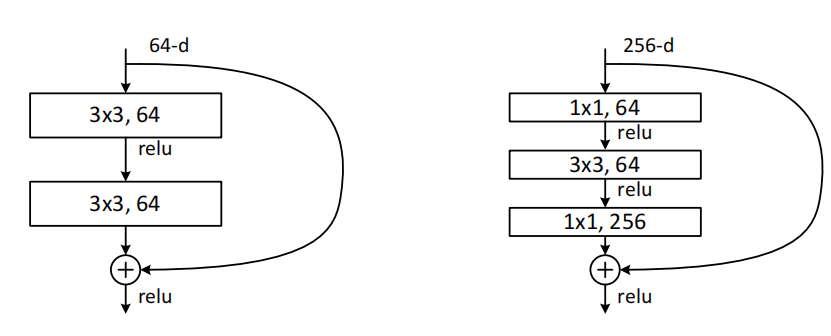
無引數的恆等shortcuts對於瓶頸結構尤為重要。如果使用對映shortcuts來替代Fig.5(右)中的恆等shortcuts，將會發現時間複雜度和模型尺寸都會增加一倍，因為shortcut連線了兩個高維端，所以恆等shortcuts對於瓶頸設計是更加有效的

層響應分析

在CIFAR-10上層響應的標準方差(std)

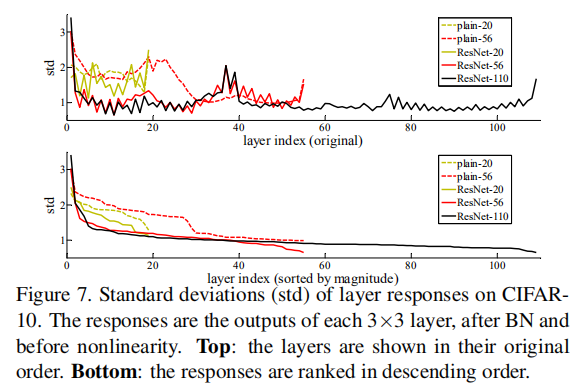
以標準方差來展示層響應，響應是每一個3*3卷積層的BN之後、非線性層(ReLU/addition)之前的輸出，實驗表明ResNets的響應比它對應的普通網路的響應要小，即殘差函式比非殘差函式更接近於0，同時越深的ResNet的響應幅度越小。當使用越多層時，ResNets中單個層對訊號的改變越少

總結

網路隨著深度的增加，訓練誤差和測試誤差非但沒有降低，反而變大了，然而這種問題的出現並不是因為過擬合，該現象被稱為退化問題(degradation problem)，本文即是為了解決深度神經網路中產生的退化問題

\(x\)作為我們的輸入，期望的輸出是\(H(x)\)，如果我們直接把輸入\(x\)傳到輸出作為初始結果，那麼我們需要學習的目標就變成了\(F(X) = H(x) - x\)。Resnet相當於將學習目標改變了，不再是學習一個完整的輸出\(H(x)\)，而是\(H(x)-x\)，即殘差，進行這樣的改變不會計算量和引數，卻能使網路更容易優化。然後，ResNet就是在原來網路的基礎上，每隔2層（或者3層，或者更多）的輸出\(F(x)\)上再加上之前的輸入\(x\)。這樣做，整個網路就可以用SGD方法進行端對端的訓練，用目前流行的深度學習庫（caffe等）也可以很容易地實現

本文提出的深度殘差學習架構，其中的構建塊為

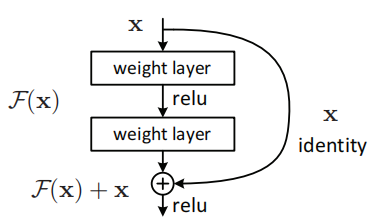
該結構的思想就是：如果增加的層能夠改善恆等對映，更深的網路應該不會比對應的淺層網路的訓練誤差大。如果恆等對映是最優的，訓練會驅使增加的非線性層的權重趨於0以靠近恆等對映

這種網路的優點有

1. 更容易優化
   
2. 網路越深，準確率越高

參考文獻

[論文閱讀] Deep Residual Learning for Image Recognition(ResNet)
Deep Residual Learning for Image Recognition(殘差網路)