QR分解

對於n階方陣A，A可逆，則存在完全QR分解，Q為n*n的正交矩陣，R為n*n的上三角矩陣。

對於非方陣的m*n(m≥n)階矩陣A，A列滿秩，存在QR分解,Q為m*n的列正交矩陣，R為n*n的上三角矩陣。

方法一：採用Gram-Schmidt法的QR分解

對於可逆矩陣A的列向量組進行Gram–Schmidt正交化，可得標準正交向量

用矩陣表達即是：

 T=(tij)，A=（），Q=()，這裡注意Q是正交矩陣。若記，則A = QR，其中T的逆矩陣R仍然是上三角矩陣

方法二：採用修正Gram-Schmidt法的QR分解

        對於Gram–Schmidt正交化求正交矩陣Q提出一種改進的計算方法，改進的地方是每產生一個單位正交向量後，就用後續的向量減去它，消去其中包含這個正交向量的部分。

       將向量標準正交化的結果取作 ，即

       然後從中減去與平行的分量，然後再標準化

        其中表示在中的投影長度。表示 —（在中的投影向量)，表示的大小，就是對應的標準正交基。

       進而，又從 除去與 和 平行的兩個分量，再進行標準正交化

以為列向量的矩陣Q與A之間有下列關係：

A=QR

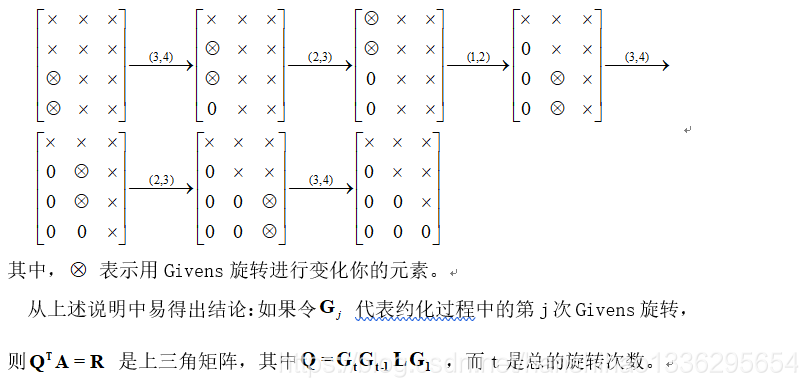
方法三：採用Givens旋轉的QR分解

 Givens旋轉也可以用來計算QR分解。以4*3的矩陣為例說明Givens QR分解的思想