旋轉矩陣的推導過程
剛體變換
定義
一個對映g:R3→R3如果滿足一下兩個特性,則是剛體變換 1. 長度保持不變:∥g(p)−g(q)=∥p−q∥, 所有p,q∈R3 2. 叉乘保持不變:g∗(v×w)=g∗(v)×g∗(w),所有向量v,w∈R3
旋轉矩陣
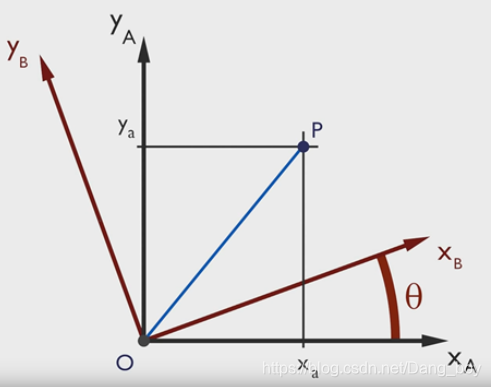
A座標系
XA=[100]T YA=[010]T
在A座標系下的B座標系
XB=cosθXA+sinθYA=[cosθ00]T+[0sinθ0]T=[cosθsinθ0]T YB=−sinθXA+cosθYA=[−sinθ00]T+[0cosθ0]T=[−sinθcosθ0]T
構造矩陣
將XBYB放到一個矩陣裡Rab=[XBYB],將之稱為旋轉矩陣
意義
將一個點的座標值在不同的基底下進行變換 P點在B座標系下為PB(a,b),可以進行一下變換 P=[XBYB][ab]=aXB+bYB=(cosθXA+sinθYA)a+(−sinθXA+cosθYA)b=[XAYA][cosθsinθ−sinθcosθ][ab]=[XAYA]Rab[ab] 可以看到,我們把基底從[XBYB]換成了[XAYA],也就是同一個點,在B座標系下的座標為[ab]T,在A座標系下的座標為R[ab]T,可以理解為是空間中同一個點在不同的座標系中(座標系旋轉了)的表示,也可以理解為同一個座標系下,是點在運動(假設座標系沒動,那麼動的就是點)。
平移變換
剛體變換除了旋轉外還有平移運動,假設變換後的座標系B的原點在原來座標系A下為PAB=[x1y1]T則 PA=RABPB+PAB 結合以上的推導,我們可以將剛體變換寫成齊次座標的形式 PA=[RAB0PAB1][PB1]
以上的推導同樣可以拓展到三維空間裡
繞Z軸旋轉的旋轉矩陣
RZ(θ)=⎣⎡cosθsinθ0−sinθcosθ0001⎦⎤
繞Y軸旋轉的旋轉矩陣
RY(θ)=⎣⎡cosθ0−sinθ010sinθ0cosθ⎦⎤
相關推薦
座標系旋轉矩陣推導過程
一、先來個平面旋轉的分析: 兩角和(差)公式 推導 旋轉變換一般是按照某個圓心點,以一定半徑 r 旋轉一定的角度α,為了簡單起見我們給出下面的情景 假定點A(x,y)想經過旋轉變換到達B(x',y'),已知旋轉角度α和點A
關於opengl中的三維矩陣平移,矩陣旋轉,推導過程理解 OpenGL計算機圖形學的一些必要矩陣運算知識 glTranslatef(x,y,z)glRotatef(angle,x,y,z)函式詳解
原文作者:aircraft 原文連結:https://www.cnblogs.com/DOMLX/p/12166896.html 為什麼引入齊次座標的變換矩陣可以表示平移呢? - Yu Mao的回答 - 知乎 https://www.zhihu.com/
旋轉矩陣的推導過程
剛體變換 定義 一個對映g:R3→R3\R^3 \to \R^3R3→R3如果滿足一下兩個特性,則是剛體變換 1. 長度保持不變:∥g(p)−g(q)=∥p−q∥\Vert g(p)-g(q)=\Vert p-q\Vert∥g(p)−g(q)=∥p−q∥, 所有
繞任意軸旋轉的矩陣推導總結
format spl 基礎 imp 平行四邊形 mage 方法 關系 建立 前言 常用的幾何變換中旋轉是較為復雜的一種,最近看《Physically Based Rendering, Second Edition: From Theory To Implementation
一分鐘詳解「本質矩陣」推導過程
前言 兩幅檢視存在兩個關係:第一種,通過對極幾何,一幅影象上的點可以確定另外一幅影象上的一條直線;另外一種,通過上一種對映,一幅影象上的點可以確定另外一幅影象上的點,這個點是第一幅影象通過光心和影象點的射線與一個平面的交點在第二幅影象上的影像。第一種情況可以用基本矩陣來表示,第二種情況則用單應矩陣來表示。而
利用SVD求得兩個對應點集合的旋轉矩陣R和轉移矩陣t的數學推導
1.問題描述 給定兩個在d維空間中對應的點集合P={p1,p2,…,pn}P={p1,p2,…,pn}和Q={q1,q2,…,qn}Q={q1,q2,…,qn},為了計算出它們之間的剛體變換,即 RR 和tt,可以將其建模為如下的數學形式: (R,t)=ar
旋轉矩陣公式推導
1.在二維平面中:如下圖所示,在xoy 平面中有一向量op⃗=(x,y) T ,旋轉ϕ 角後變為向量op⃗ ′ =(x ′ ,y ′ ) T 。 據圖可得:x=|op⃗|c
解釋一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推導過程(轉載)
線性不可分 itl 專註 out center forest 測試 重要 原因 KPCA,中文名稱”核主成分分析“,是對PCA算法的非線性擴展,言外之意,PCA是線性的,其對於非線性數據往往顯得無能為力,例如,不同人之間的人臉圖像,肯定存在非線性關系,自己做的基於ORL數據
順時針旋轉矩陣
編寫 eight pre ret -c article ++ nbsp 初始 題目描述 有一個NxN整數矩陣,請編寫一個算法,將矩陣順時針旋轉90度。 給定一個NxN的矩陣,和矩陣的階數N,請返回旋轉後的NxN矩陣,保證N小於等於300。 測試樣例: [[1,2,3],
簡單三維空間的旋轉矩陣的計算
tps ota bsp rotation -a mat tar 空間 stack 主要參考 原文鏈接:https://math.stackexchange.com/questions/180418/calculate-rotation-matrix-to-align-ve
OpenGL ES平移矩陣和旋轉矩陣的左乘與右乘效果
角度 style 位置 作用 span 坐標系 rotate 不同的 世界 OpenGL ES平移矩陣和旋轉矩陣的左乘與右乘 在OpenGL 、OpenGL ES中矩陣起著舉足輕重的作用,而矩陣之間的左乘與右乘在效果上是不同的。 一、先平移後旋轉 場景效果:人繞樹旋轉。 原
三個歐拉角得到3x3旋轉矩陣
三維空間 ont pre sin cos rotation mic ati div 三維坐標系中,已知三個歐拉角alpha,beta,gamma,分別為繞x軸旋轉alpha角度,繞y軸旋轉beta角度,繞z軸旋轉gamma角度。則旋轉矩陣Rotation的求法如下: Ma
三維空間旋轉(歐拉角、四元數、旋轉矩陣)
轉換 當我 隨著 www href bsp out 組合 相同 姿態角(歐拉角) 姿態角即RPY(roll, pitch,yaw)又叫歐拉角,是由三個角組成的。 俯仰角(pitch) 翻滾角(roll) 偏航角(yaw) 其中最
SVM推導過程
SVM 機器學習 SVM推導過程
神經網絡的BP推導過程
size 附錄 strong 如何 技術分享 由於 pan 設置 預測 神經網絡的BP推導過程 下面我們從一個簡單的例子入手考慮如何從數學上計算代價函數的梯度,考慮如下簡單的神經網絡,該神經網絡有三層神經元,對應的兩個權重矩陣,為了計算梯度我們只需要計算兩個偏導數即可:
旋轉矩陣 軸角 尤拉角 四元數
引言 我們日常生活的空間是三維的,因此我們生來就習慣於空間的運動。三維空間由三個軸組成,所以一個空間點的位置可以由3個座標指定。不過,我們現在要考慮剛體,它不光有位置,還有自身的姿態。以下,就是對剛體姿態的相關學習的筆記。 旋轉矩陣 表示座標系`O-x'y'z'`中
三維座標變換——旋轉矩陣與旋轉向量
https://blog.csdn.net/mightbxg/article/details/79363699 用 opencv 進行過雙目相機標定的同學都知道,單目標定 calibrateCamera() 函式能夠對每一張標定影象計算出一對 rvec 和 tvec,即旋轉平移向量,代表世界座標
四元數與旋轉矩陣——SLAM
1. 用四元數表示旋轉時,都是單位四元數。 2. 用四元數表示旋轉時,三維空間的點p(x,y,z)需要表示成虛四元數,即。 3. 四元數導數與角速度之間的關係 :表示local座標系到global座標系的旋轉; &n
簡單線性迴歸-最小二乘法推導過程
最近學習線性迴歸,自己推導了一下最小二乘法。 其他參考文章: https://blog.csdn.net/chasdmeng/article/details/38869941?utm_source=blogxgwz0 https://blog.csdn.net/iter
卡爾曼濾波的理解以及推導過程
針對的系統為: 狀態方程 X(k)=AX(k-1)+Bu(k-1)+W(k-1) 測量方程 Z(k)=HX(k)+V(k) &
