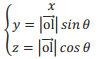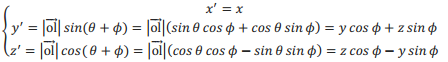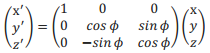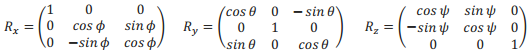1.在二維平面中：如下圖所示，在xoy 平面中有一向量op⃗=(x,y) T  ，旋轉ϕ 角後變為向量op⃗ ′ =(x ′ ,y ′ ) T  。
　　

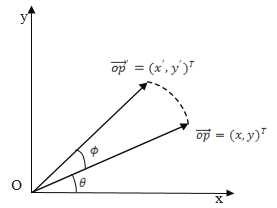
　　據圖可得：x=|op⃗|cosθ；y=|op⃗|sinθ ，經旋轉ϕ 角後有:
　　x ′ =|op⃗|cos(θ+ϕ)=|op⃗|(cosθcosϕ−sinθsinϕ)=xcosϕ−ysinϕ 
　　y ′ =|op⃗|sin(θ+ϕ)=|op⃗|(sinθcosϕ+cosθsinϕ)=xsinϕ+ycosϕ； 
寫成矩陣形式：
　　(x ′ y ′  )=(cosϕsinϕ −sinϕcosϕ )(xy ) 

　　2.在三維空間中：如下圖所示，若以座標系的三個座標軸X、Y、Z分別作為旋轉軸，則點實際上只在垂直座標軸的平面上作二維旋轉。

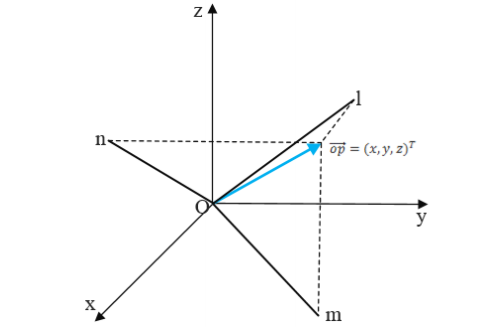
　　例： op⃗ 繞X軸旋轉ϕ 角，有：
旋轉前：
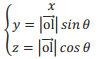
旋轉後：
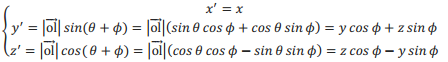
寫成矩陣形式：
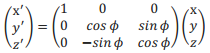
則繞X軸旋ϕ角的旋轉矩陣為： R x (ϕ)=（100 0cosϕ−sinϕ 0sinϕcosϕ ） 
同理可得繞X、Y、Z軸旋轉的不同角度的旋轉矩陣（方向餘弦矩陣）分別為：

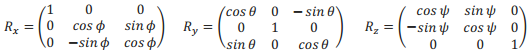
　　最後，若op⃗ 繞某一定軸旋轉，從尤拉定律中可知，繞著固定軸做一個角值的旋轉，可以被視為分別以座標系的三個座標軸X、Y、Z作為旋轉軸的旋轉的疊加。