Hough transform(霍夫變換)
主要內容：
1、Hough變換的演算法思想
2、直線檢測
3、圓、橢圓檢測
4、程式實現
一、Hough變換簡介
Hough變換是影象處理中從影象中識別幾何形狀的基本方法之一。Hough變換的基本原理在於利用點與線的對偶性，將原始影象空間的給定的曲線通過曲線表達形式變為引數空間的一個點。這樣就把原始影象中給定曲線的檢測問題轉化為尋找引數空間中的峰值問題。也即把檢測整體特性轉化為檢測區域性特性。比如直線、橢圓、圓、弧線等。
霍夫變換於1962年由Paul Hough 首次提出[53]，後於1972年由Richard Duda和Peter Hart推廣使用[54]，經典霍夫變換用來檢測影象中的直線，後來霍夫變換擴充套件到任意形狀物體的識別，多為圓和橢圓。
1.1 直線檢測
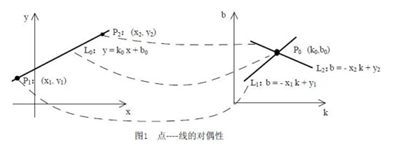
設已知一黑白影象上畫了一條直線，要求出這條直線所在的位置。我們知道，直線的方程可以用y=k*x+b 來表示，其中k和b是引數，分別是斜率和截距。過某一點(x0,y0)的所有直線的引數都會滿足方程y0=kx0+b。即點(x0,y0)確定了一族直線。方程y0=kx0+b在引數k--b平面上是一條直線，(你也可以是方程b=-x0*k+y0對應的直線)。這樣，影象x--y平面上的一個前景畫素點就對應到引數平面上的一條直線。我們舉個例子說明解決前面那個問題的原理。設影象上的直線是y=x, 我們先取上面的三個點：A(0,0), B(1,1), C(22)。可以求出，過A點的直線的引數要滿足方程b=0, 過B點的直線的引數要滿足方程1=k+b, 過C點的直線的引數要滿足方程2=2k+b, 這三個方程就對應著引數平面上的三條直線，而這三條直線會相交於一點(k=1,b=0)。 同理，原影象上直線y=x上的其它點(如(3,3),(4,4)等) 對應引數平面上的直線也會通過點(k=1,b=0)。這個性質就為我們解決問題提供了方法，就是把影象平面上的點對應到引數平面上的線，最後通過統計特性來解決問題。假如影象平面上有兩條直線，那麼最終在引數平面上就會看到兩個峰值點，依此類推。
簡而言之，Hough變換思想為：在原始影象座標系下的一個點對應了引數座標系中的一條直線，同樣引數座標系的一條直線對應了原始座標系下的一個點，然後，原始座標系下呈現直線的所有點，它們的斜率和截距是相同的，所以它們在引數座標系下對應於同一個點。這樣在將原始座標系下的各個點投影到引數座標系下之後，看引數座標系下有沒有聚集點，這樣的聚集點就對應了原始座標系下的直線。
在實際應用中，y=k*x+b形式的直線方程沒有辦法表示x=c形式的直線(這時候，直線的斜率為無窮大)。所以實際應用中，是採用引數方程p=x*cos(theta)+y*sin(theta)。這樣，影象平面上的一個點就對應到引數p---theta平面上的一條曲線上，其它的還是一樣。
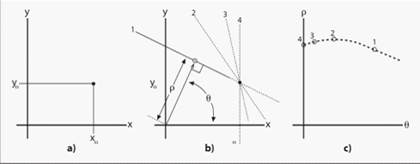
上圖（a）所示為原始的影象空間中一個點
；（b）所示為直角座標系當中為過同一四條直線；（c）所示為這四條直線在極座標引數空間可以表示為四個點
為了檢測出直角座標X-Y中由點所構成的直線，可以將極座標a-p量化成許多小格。根據直角座標中每個點的座標(x,y)，在a = 0-180°內以小格的步長計算各個p值，所得值落在某個小格內，便使該小格的累加記數器加1。當直角座標中全部的點都變換後，對小格進行檢驗，計數值最大的小格，其(a，p)值對應於直角座標中所求直線。
思路解析：
1）讀取一幅帶處理二值影象，最好背景為黑色；
2）獲取影象空間的源畫素資料；
3）通過量化霍夫引數空間為有限個值間隔等分或者累加格子，即p,theta；
4）霍夫變換演算法開始，每個畫素座標點P(x, y)被轉換到(r, theta)的曲線點上面，並累加到對應的格子資料點；
5）尋找最大霍夫值，設定閾值，反變換到影象空間；
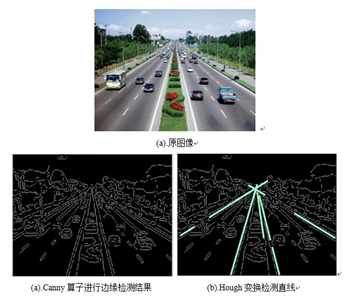
實際應用例子:車道檢測
1.2 已知半徑的圓
其實Hough變換可以檢測任意的已知表達形式的曲線，關鍵是看其引數空間的選擇，引數空間的選擇可以根據它的表達形式而定。比如圓的表達形式為 ，所以當檢測某一半徑的圓的時候，可以選擇與原影象空間同樣的空間作為引數空間。那麼圓影象空間中的一個圓對應了引數空間中的一個點，引數空間中的一個點對應了影象空間中的一個圓，圓影象空間中在同一個圓上的點，它們的引數相同即a，b相同，那麼它們在引數空間中的對應的圓就會過同一個點（a，b），所以，將原影象空間中的所有點變換到引數空間後，根據引數空間中點的聚集程度就可以判斷出影象空間中有沒有近似於圓的圖形。如果有的話，這個引數就是圓的引數。
1.3 未知半徑的圓
對於圓的半徑未知的情況下，可以看作是有三個引數的圓的檢測，中心和半徑。這個時候原理仍然相同，只是引數空間的維數升高，計算量增大。影象空間中的任意一個點都對應了引數空間中的一簇圓曲線。 ，其實是一個圓錐型。引數空間中的任意一個點對應了影象空間中的一個圓。
1.4 橢圓
橢圓有5個自由引數，所以它的引數空間是5維的，因此他的計算量非常大，所以提出了許多的改進演算法。
二、程式實現
對於處理一般影象，需要對影象進行邊緣檢測和二值化處理,Hough變換的輸入是黑白二值影象。
matlab：
openCV:
三、總結
影象空間中的在同一個圓，直線，橢圓上的點，每一個點都對應了引數空間中的一個圖形，在影象空間中這些點都滿足它們的方程這一個條件，所以這些點，每個投影后得到的影象都會經過這個引數空間中的點。也就是在引數空間中它們會相交於一點。所以，當引數空間中的這個相交點的越大的話，那麼說明元影象空間中滿足這個引數的圖形越飽滿。越象我們要檢測的東西。
Hough變換能夠查詢任意的曲線，只要你給定它的方程。Hough變換在檢驗已知形狀的目標方面具有受曲線間斷影響小和不受圖形旋轉的影響的優點，即使目標有稍許缺損或汙染也能被正確識別。