摘要：

　　大師 L. Peter Deutsch 說過：To Iterate is Human, to Recurse, Divine.中文譯為：人理解迭代，神理解遞迴。毋庸置疑地，遞迴確實是一個奇妙的思維方式。對一些簡單的遞迴問題，我們總是驚歎於遞迴描述問題的能力和編寫程式碼的簡潔，但要想真正領悟遞迴的精髓、靈活地運用遞迴思想來解決問題卻並不是一件容易的事情。本文剖析了遞迴的思想內涵，分析了遞迴與迴圈的聯絡與區別，給出了遞迴的應用場景和一些典型應用，並利用遞迴和非遞迴的方式解決了包括階乘、斐波那契數列、漢諾塔、楊輝三角的存取、字串迴文判斷、字串全排列、二分查詢、樹的深度求解在內的八個經典問題。

友情提示：

一. 引子

　　 大師 L. Peter Deutsch 說過：To Iterate is Human, to Recurse, Divine.中文譯為：人理解迭代，神理解遞迴。毋庸置疑地，遞迴確實是一個奇妙的思維方式。對一些簡單的遞迴問題，我們總是驚歎於遞迴描述問題的能力和編寫程式碼的簡潔，但要想真正領悟遞迴的精髓、靈活地運用遞迴思想來解決問題卻並不是一件容易的事情。在正式介紹遞迴之前，我們首先引用知乎使用者李繼剛(https://www.zhihu.com/question/20507130/answer/15551917)對遞迴和迴圈的生動解釋：

　　 遞迴：你打開面前這扇門，看到屋裡面還有一扇門。你走過去，發現手中的鑰匙還可以開啟它，你推開門，發現裡面還有一扇門，你繼續開啟它。若干次之後，你打開面前的門後，發現只有一間屋子，沒有門了。然後，你開始原路返回，每走回一間屋子，你數一次，走到入口的時候，你可以回答出你到底用這你把鑰匙打開了幾扇門。

　　 迴圈：你打開面前這扇門，看到屋裡面還有一扇門。你走過去，發現手中的鑰匙還可以開啟它，你推開門，發現裡面還有一扇門（若前面兩扇門都一樣，那麼這扇門和前兩扇門也一樣；如果第二扇門比第一扇門小，那麼這扇門也比第二扇門小，你繼續開啟這扇門，一直這樣繼續下去直到開啟所有的門。但是，入口處的人始終等不到你回去告訴他答案。

　　 上面的比喻形象地闡述了遞迴與迴圈的內涵，那麼我們來思考以下幾個問題：

什麼是遞迴呢？  遞迴的精髓(思想)是什麼？  遞迴和迴圈的區別是什麼？  什麼時候該用遞迴？  使用遞迴需要注意哪些問題？  遞迴思想解決了哪些經典的問題？  這些問題正是筆者準備在本文中詳細闡述的問題。

二. 遞迴的內涵

1、定義 (什麼是遞迴？)

　　 在數學與電腦科學中，遞迴(Recursion)是指在函式的定義中使用函式自身的方法。實際上，遞迴，顧名思義，其包含了兩個意思：遞 和 歸，這正是遞迴思想的精華所在。

2、遞迴思想的內涵(遞迴的精髓是什麼？)

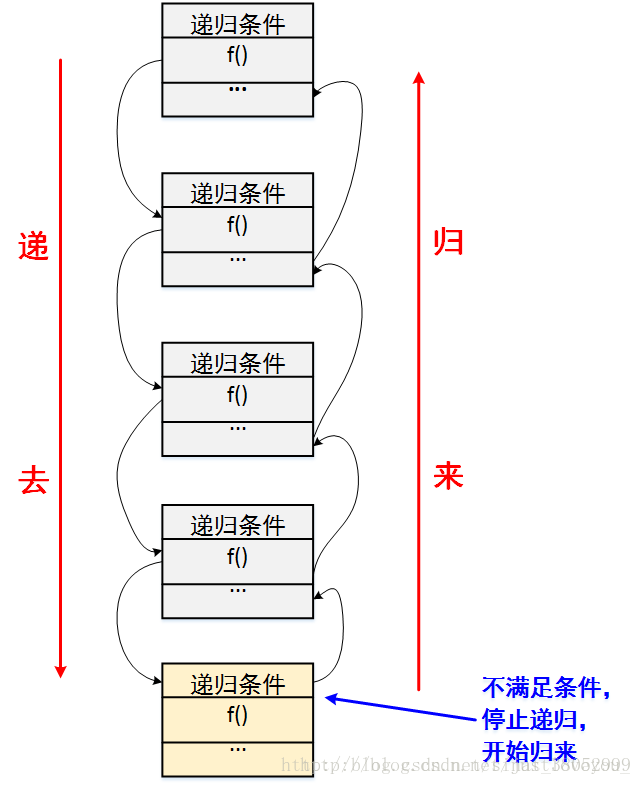
　　 正如上面所描述的場景，遞迴就是有去（遞去）有回（歸來），如下圖所示。“有去”是指：遞迴問題必須可以分解為若干個規模較小，與原問題形式相同的子問題，這些子問題可以用相同的解題思路來解決，就像上面例子中的鑰匙可以開啟後面所有門上的鎖一樣；“有回”是指 : 這些問題的演化過程是一個從大到小，由近及遠的過程，並且會有一個明確的終點(臨界點)，一旦到達了這個臨界點，就不用再往更小、更遠的地方走下去。最後，從這個臨界點開始，原路返回到原點，原問題解決。　　

　　  　　 更直接地說，遞迴的基本思想就是把規模大的問題轉化為規模小的相似的子問題來解決。特別地，在函式實現時，因為解決大問題的方法和解決小問題的方法往往是同一個方法，所以就產生了函式呼叫它自身的情況，這也正是遞迴的定義所在。格外重要的是，這個解決問題的函式必須有明確的結束條件，否則就會導致無限遞迴的情況。

3、用歸納法來理解遞迴

　　 數學都不差的我們，第一反應就是遞迴在數學上的模型是什麼，畢竟我們對於問題進行數學建模比起程式碼建模拿手多了。觀察遞迴，我們會發現，遞迴的數學模型其實就是 數學歸納法，這個在高中的數列裡面是最常用的了，下面回憶一下數學歸納法。

　　 數學歸納法適用於將解決的原問題轉化為解決它的子問題，而它的子問題又變成子問題的子問題，而且我們發現這些問題其實都是一個模型，也就是說存在相同的邏輯歸納處理項。當然有一個是例外的，也就是歸納結束的那一個處理方法不適用於我們的歸納處理項，當然也不能適用，否則我們就無窮歸納了。總的來說，歸納法主要包含以下三個關鍵要素：

步進表示式：問題蛻變成子問題的表示式  結束條件：什麼時候可以不再使用步進表示式  直接求解表示式：在結束條件下能夠直接計算返回值的表示式  事實上，這也正是某些數學中的數列問題在利用程式設計的方式去解決時可以使用遞迴的原因，比如著名的斐波那契數列問題。

4、遞迴的三要素

　　 在我們瞭解了遞迴的基本思想及其數學模型之後，我們如何才能寫出一個漂亮的遞迴程式呢？筆者認為主要是把握好如下三個方面：

1、明確遞迴終止條件；

2、給出遞迴終止時的處理辦法；

3、提取重複的邏輯，縮小問題規模。

1). 明確遞迴終止條件

　　 我們知道，遞迴就是有去有回，既然這樣，那麼必然應該有一個明確的臨界點，程式一旦到達了這個臨界點，就不用繼續往下遞去而是開始實實在在的歸來。換句話說，該臨界點就是一種簡單情境，可以防止無限遞迴。

2). 給出遞迴終止時的處理辦法

　　 我們剛剛說到，在遞迴的臨界點存在一種簡單情境，在這種簡單情境下，我們應該直接給出問題的解決方案。一般地，在這種情境下，問題的解決方案是直觀的、容易的。

3). 提取重複的邏輯，縮小問題規模*

　　 我們在闡述遞迴思想內涵時談到，遞迴問題必須可以分解為若干個規模較小、與原問題形式相同的子問題，這些子問題可以用相同的解題思路來解決。從程式實現的角度而言，我們需要抽象出一個乾淨利落的重複的邏輯，以便使用相同的方式解決子問題。

5、遞迴演算法的程式設計模型

　　 在我們明確遞迴演算法設計三要素後，接下來就需要著手開始編寫具體的演算法了。在編寫演算法時，不失一般性，我們給出兩種典型的遞迴演算法設計模型，如下所示。

模型一： 在遞去的過程中解決問題

function recursion(大規模){
    if (end_condition){      // 明確的遞迴終止條件
        end;   // 簡單情景
    }else{            // 在將問題轉換為子問題的每一步，解決該步中剩餘部分的問題
        solve;                // 遞去
        recursion(小規模);     // 遞到最深處後，不斷地歸來
    }
}

模型二： 在歸來的過程中解決問題

function recursion(大規模){
    if (end_condition){      // 明確的遞迴終止條件
        end;   // 簡單情景
    }else{            // 先將問題全部描述展開，再由盡頭“返回”依次解決每步中剩餘部分的問題
        recursion(小規模);     // 遞去
        solve;                // 歸來
    }
}

6、遞迴的應用場景

　　 在我們實際學習工作中，遞迴演算法一般用於解決三類問題：

　　 (1). 問題的定義是按遞迴定義的（Fibonacci函式，階乘，…）；

　　 (2). 問題的解法是遞迴的（有些問題只能使用遞迴方法來解決，例如，漢諾塔問題，…）；

　　 (3). 資料結構是遞迴的（連結串列、樹等的操作，包括樹的遍歷，樹的深度，…）。

　　在下文我們將給出遞迴演算法的一些經典應用案例，這些案例基本都屬於第三種類型問題的範疇。

三. 遞迴與迴圈

　　 遞迴與迴圈是兩種不同的解決問題的典型思路。遞迴通常很直白地描述了一個問題的求解過程，因此也是最容易被想到解決方式。迴圈其實和遞迴具有相同的特性，即做重複任務，但有時使用迴圈的演算法並不會那麼清晰地描述解決問題步驟。單從演算法設計上看，遞迴和迴圈並無優劣之別。然而，在實際開發中，因為函式呼叫的開銷，遞迴常常會帶來效能問題，特別是在求解規模不確定的情況下；而迴圈因為沒有函式呼叫開銷，所以效率會比遞迴高。遞迴求解方式和迴圈求解方式往往可以互換，也就是說，如果用到遞迴的地方可以很方便使用迴圈替換，而不影響程式的閱讀，那麼替換成迴圈往往是好的。問題的遞迴實現轉換成非遞迴實現一般需要兩步工作：

　　 (1). 自己建立“堆疊(一些區域性變數)”來儲存這些內容以便代替系統棧，比如樹的三種非遞迴遍歷方式；

　　 (2). 把對遞迴的呼叫轉變為對迴圈處理。

　　 特別地，在下文中我們將給出遞迴演算法的一些經典應用案例，對於這些案例的實現，我們一般會給出遞迴和非遞迴兩種解決方案，以便讀者體會。

四. 經典遞迴問題實戰

1. 第一類問題：問題的定義是按遞迴定義的

(1). 階乘

/**
 * Title: 階乘的實現 
 * Description:
 *      遞迴解法
 *      非遞迴解法
 * @author rico
 */
public class Factorial {
    /**     
     * @description 階乘的遞迴實現
     * @author rico       
     * @created 2017年5月10日 下午8:45:48     
     * @param n
     * @return     
     */
    public static long f(int n){
        if(n == 1)   // 遞迴終止條件 
            return 1;    // 簡單情景

        return n*f(n-1);  // 相同重複邏輯，縮小問題的規模
    }

--------------------------------我是分割線-------------------------------------

    /**     
     * @description 階乘的非遞迴實現
     * @author rico       
     * @created 2017年5月10日 下午8:46:43     
     * @param n
     * @return     
     */
    public static long f_loop(int n) {
        long result = n;
        while (n > 1) {
            n--;
            result = result * n;
        }
        return result;
    }
}

(2). 斐波納契數列

/**  * Title: 斐波納契數列  *  * Description: 斐波納契數列，又稱黃金分割數列，指的是這樣一個數列：1、1、2、3、5、8、13、21、……  * 在數學上，斐波納契數列以如下被以遞迴的方法定義：F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2，n∈N*）。  *  * 兩種遞迴解法：經典解法和優化解法  * 兩種非遞迴解法：遞推法和陣列法  *

 * @author rico
 */
public class FibonacciSequence {

    /**
     * @description 經典遞迴法求解
     * 
     * 斐波那契數列如下：
     * 
     *  1,1,2,3,5,8,13,21,34,...
     * 
     * *那麼，計算fib(5)時，需要計算1次fib(4),2次fib(3),3次fib(2)，呼叫了2次fib(1)*，即：
     * 
     *  fib(5) = fib(4) + fib(3)
     *  
     *  fib(4) = fib(3) + fib(2) ；fib(3) = fib(2) + fib(1)
     *  
     *  fib(3) = fib(2) + fib(1)
     *  
     * 這裡麵包含了許多重複計算，而實際上我們只需計算fib(4)、fib(3)、fib(2)和fib(1)各一次即可，
     * 後面的optimizeFibonacci函式進行了優化，使時間複雜度降到了O(n).
     * 
     * @author rico
     * @created 2017年5月10日 下午12:00:42
     * @param n
     * @return
     */
    public static int fibonacci(int n) {
        if (n == 1 || n == 2) {     // 遞迴終止條件
            return 1;       // 簡單情景
        }
        return fibonacci(n - 1) + fibonacci(n - 2); // 相同重複邏輯，縮小問題的規模
    }

——————————–我是分割線————————————-

/**     
 * @description 對經典遞迴法的優化
 * 
 * 斐波那契數列如下：
 * 
 *  1,1,2,3,5,8,13,21,34,...
 * 
 * 那麼，我們可以這樣看：fib(1,1,5) = fib(1,2,4) = fib(2,3,3) = 5
 * 
 * 也就是說，以1,1開頭的斐波那契數列的第五項正是以1,2開頭的斐波那契數列的第四項，
 * 而以1,2開頭的斐波那契數列的第四項也正是以2,3開頭的斐波那契數列的第三項，
 * 更直接地，我們就可以一步到位：fib(2,3,3) = 2 + 3 = 5,計算結束。 
 * 
 * 注意，前兩個引數是數列的開頭兩項，第三個引數是我們想求的以前兩個引數開頭的數列的第幾項。
 * 

    * 時間複雜度：O(n)
     * 
     * @author rico       
     * @param first 數列的第一項
     * @param second 數列的第二項
     * @param n 目標項
     * @return     
     */
    public static int optimizeFibonacci(int first, int second, int n) {
        if (n > 0) {
            if(n == 1){    // 遞迴終止條件
                return first;       // 簡單情景
            }else if(n == 2){            // 遞迴終止條件
                return second;      // 簡單情景
            }else if (n == 3) {         // 遞迴終止條件
                return first + second;      // 簡單情景
            }
            return optimizeFibonacci(second, first + second, n - 1);  // 相同重複邏輯，縮小問題規模
        }
        return -1;
    }

--------------------------------我是分割線-------------------------------------

    /**
     * @description 非遞迴解法：有去無回
     * @author rico
     * @created 2017年5月10日 下午12:03:04
     * @param n
     * @return
     */
    public static int fibonacci_loop(int n) {

        if (n == 1 || n == 2) {   
            return 1;
        }

        int result = -1;
        int first = 1;      // 自己維護的"棧",以便狀態回溯
        int second = 1;     // 自己維護的"棧",以便狀態回溯

        for (int i = 3; i <= n; i++) { // 迴圈
            result = first + second;
            first = second;
            second = result;
        }
        return result;
    }

--------------------------------我是分割線-------------------------------------

/**     
     * @description 使用陣列儲存斐波那契數列
     * @author rico       
     * @param n
     * @return     
     */
    public static int fibonacci_array(int n) {
        if (n > 0) {
            int[] arr = new int[n];   // 使用臨時陣列儲存斐波納契數列
            arr[0] = arr[1] = 1;

            for (int i = 2; i < n; i++) {   // 為臨時陣列賦值
                arr[i] = arr[i-1] + arr[i-2];
            }
            return arr[n - 1];
        }
        return -1;
    }
}

(3). 楊輝三角的取值

/**     
 * @description 遞迴獲取楊輝三角指定行、列(從0開始)的值
 *              注意：與是否建立楊輝三角無關

    * @author rico 
     * @x  指定行
     * @y  指定列    
     */
  /**
    * Title: 楊輝三角形又稱Pascal三角形，它的第i+1行是(a+b)i的展開式的係數。
    * 它的一個重要性質是：三角形中的每個數字等於它兩肩上的數字相加。
    * 
    * 例如，下面給出了楊輝三角形的前4行： 
    *    1 
    *   1 1
    *  1 2 1
    * 1 3 3 1
    * @description 遞迴獲取楊輝三角指定行、列(從0開始)的值
    *              注意：與是否建立楊輝三角無關
    * @author rico 
    * @x  指定行
    * @y  指定列  
    */
    public static int getValue(int x, int y) {
        if(y <= x && y >= 0){
            if(y == 0 || x == y){   // 遞迴終止條件
                return 1; 
            }else{ 
                // 遞迴呼叫，縮小問題的規模
                return getValue(x-1, y-1) + getValue(x-1, y); 
            }
        }
        return -1;
    } 
}

(4). 迴文字串的判斷

/**  * Title: 迴文字串的判斷  * Description: 迴文字串就是正讀倒讀都一樣的字串。如”98789”, “abccba”都是迴文字串  *  * 兩種解法：  * 遞迴判斷；  * 迴圈判斷；  *

 * @author rico       
 */      
public class PalindromeString {

    /**     
     * @description 遞迴判斷一個字串是否是迴文字串
     * @author rico       
     * @created 2017年5月10日 下午5:45:50     
     * @param s
     * @return     
     */
    public static boolean isPalindromeString_recursive(String s){
        int start = 0;
        int end = s.length()-1;
        if(end > start){   // 遞迴終止條件:兩個指標相向移動，當start超過end時，完成判斷
            if(s.charAt(start) != s.charAt(end)){
                return false;
            }else{
                // 遞迴呼叫，縮小問題的規模
                return isPalindromeString_recursive(s.substring(start+1).substring(0, end-1));
            }
        }
        return true;
    }

--------------------------------我是分割線-------------------------------------

    /**     
     * @description 迴圈判斷迴文字串
     * @author rico       
     * @param s
     * @return     
     */
    public static boolean isPalindromeString_loop(String s){
        char[] str = s.toCharArray();
        int start = 0;
        int end = str.length-1;
        while(end > start){  // 迴圈終止條件:兩個指標相向移動，當start超過end時，完成判斷
            if(str[end] != str[start]){
                return false;
            }else{
                end --;
                start ++;
            }
        }
        return true;
    }
}

(5). 字串全排列

遞迴解法  /**  * @description 從字串陣列中每次選取一個元素，作為結果中的第一個元素;然後，對剩餘的元素全排列

     * @author rico
     * @param s
     *            字元陣列
     * @param from
     *            起始下標
     * @param to
     *            終止下標
     */
    public static void getStringPermutations3(char[] s, int from, int to) {
        if (s != null && to >= from && to < s.length && from >= 0) { // 邊界條件檢查
            if (from == to) { // 遞迴終止條件
                System.out.println(s); // 列印結果
            } else {
                for (int i = from; i <= to; i++) {
                    swap(s, i, from); // 交換字首,作為結果中的第一個元素，然後對剩餘的元素全排列
                    getStringPermutations3(s, from + 1, to); // 遞迴呼叫，縮小問題的規模
                    swap(s, from, i); // 換回字首，復原字元陣列
                }
            }
        }
    }

    /**
     * @description 對字元陣列中的制定字元進行交換
     * @author rico
     * @param s
     * @param from
     * @param to
     */
    public static void swap(char[] s, int from, int to) {
        char temp = s[from];
        s[from] = s[to];
        s[to] = temp;
    }

非遞迴解法(字典序全排列)  /**  * Title: 字串全排列非遞迴演算法(字典序全排列)  * Description: 字典序全排列，其基本思想是：  * 先對需要求排列的字串進行字典排序，即得到全排列中最小的排列.  * 然後,找到一個比它大的最小的全排列，一直重複這一步直到找到最大值,即字典排序的逆序列.  *  * 不需要關心字串長度  *  * @author rico  */  public class StringPermutationsLoop {

/**
 * @description 字典序全排列
 * 
 * 設一個字串(字元陣列)的全排列有n個，分別是A1,A2,A3,...,An
 * 
 * 1. 找到最小的排列 Ai
 * 2. 找到一個比Ai大的最小的後繼排列Ai+1
 * 3. 重複上一步直到沒有這樣的後繼
 * 
 * 重點就是如何找到一個排列的直接後繼:
 * 對於字串(字元陣列)a0a1a2……an,
 * 1. 從an到a0尋找第一次出現的升序排列的兩個字元(即ai < ai+1),那麼ai+1是一個極值，因為ai+1之後的字元為降序排列，記 top=i+1;
 * 2. 從top處(包括top)開始查詢比ai大的最小的值aj，記 minMax = j;
 * 3. 交換minMax處和top-1處的字元;
 * 4. 翻轉top之後的字元(包括top)，即得到一個排列的直接後繼排列
 * 

  * @author rico
     * @param s
     *            字元陣列
     * @param from
     *            起始下標
     * @param to
     *            終止下標
     */
    public static void getStringPermutations4(char[] s, int from, int to) {

        Arrays.sort(s,from,to+1);  // 對字元陣列的所有元素進行升序排列，即得到最小排列 
        System.out.println(s);    

        char[] descendArr = getMaxPermutation(s, from, to); // 得到最大排列,即最小排列的逆序列

        while (!Arrays.equals(s, descendArr)) {  // 迴圈終止條件：迭代至最大排列
            if (s != null && to >= from && to < s.length && from >= 0) { // 邊界條件檢查
                int top = getExtremum(s, from, to); // 找到序列的極值
                int minMax = getMinMax(s, top, to);  // 從top處(包括top)查詢比s[top-1]大的最小值所在的位置
                swap(s, top - 1, minMax);  // 交換minMax處和top-1處的字元
                s = reverse(s, top, to);   // 翻轉top之後的字元
                System.out.println(s);
            }
        }
    }

    /**
     * @description 對字元陣列中的制定字元進行交換
     * @author rico
     * @param s
     * @param from
     * @param to
     */
    public static void swap(char[] s, int from, int to) {
        char temp = s[from];
        s[from] = s[to];
        s[to] = temp;
    }

    /**     
     * @description 獲取序列的極值
     * @author rico       
     * @param s 序列
     * @param from 起始下標
     * @param to 終止下標
     * @return     
     */
    public static int getExtremum(char[] s, int from, int to) {
        int index = 0;
        for (int i = to; i > from; i--) {
            if (s[i] > s[i - 1]) {
                index = i;
                break;
            }
        }
        return index;
    }

    /**     
     * @description 從top處查詢比s[top-1]大的最小值所在的位置
     * @author rico       
     * @created 2017年5月10日 上午9:21:13     
     * @param s
     * @param top 極大值所在位置
     * @param to
     * @return     
     */
    public static int getMinMax(char[] s, int top, int to) {
        int index = top;
        char base = s[top-1];
        char temp = s[top];
        for (int i = top + 1; i <= to; i++) {
            if (s[i] > base && s[i] < temp) {
                temp = s[i];
                index = i;
            }
            continue;
        }
        return index;
    }

    /**     
     * @description 翻轉top(包括top)後的序列
     * @author rico       
     * @param s
     * @param from
     * @param to
     * @return     
     */
    public static char[] reverse(char[] s, int top, int to) {
        char temp;
        while(top < to){
            temp = s[top];
            s[top] = s[to];
            s[to] = temp;
            top ++;
            to --;
        }
        return s;
    }

    /**     
     * @description 根據最小排列得到最大排列
     * @author rico       
     * @param s 最小排列
     * @param from 起始下標
     * @param to 終止下標
     * @return     
     */
    public static char[] getMaxPermutation(char[] s, int from, int to) {
        //將最小排列複製到一個新的陣列中
        char[] dsc = Arrays.copyOfRange(s, 0, s.length);
        int first = from;
        int end = to;
        while(end > first){  // 迴圈終止條件
            char temp = dsc[first];
            dsc[first] = dsc[end];
            dsc[end] = temp;
            first ++;
            end --;
        }
        return dsc;
    }

(6). 二分查詢

/**  * @description 二分查詢的遞迴實現  * @author rico  * @param array 目標陣列  * @param low 左邊界  * @param high 右邊界  * @param target 目標值  * @return 目標值所在位置  */

public static int binarySearch(int[] array, int low, int high, int target) {

        //遞迴終止條件
        if(low <= high){
            int mid = (low + high) >> 1;
            if(array[mid] == target){
                return mid + 1;  // 返回目標值的位置，從1開始
            }else if(array[mid] > target){
                // 由於array[mid]不是目標值，因此再次遞迴搜尋時，可以將其排除
                return binarySearch(array, low, mid-1, target);
            }else{
                // 由於array[mid]不是目標值，因此再次遞迴搜尋時，可以將其排除
                return binarySearch(array, mid+1, high, target);
            }
        }
        return -1;   //表示沒有搜尋到
    }

--------------------------------我是分割線-------------------------------------

/**     
     * @description 二分查詢的非遞迴實現
     * @author rico       
     * @param array 目標陣列
     * @param low 左邊界
     * @param high 右邊界
     * @param target 目標值
     * @return 目標值所在位置
     */
public static int binarySearchNoRecursive(int[] array, int low, int high, int target) {

        // 迴圈
        while (low <= high) {
            int mid = (low + high) >> 1;
            if (array[mid] == target) {
                return mid + 1; // 返回目標值的位置，從1開始
            } else if (array[mid] > target) {
                // 由於array[mid]不是目標值，因此再次遞迴搜尋時，可以將其排除
                high = mid -1;
            } else {
                // 由於array[mid]不是目標值，因此再次遞迴搜尋時，可以將其排除
                low = mid + 1;
            }
        }
        return -1;  //表示沒有搜尋到
    }

1. 第二類問題：問題解法按遞迴演算法實現

(1). 漢諾塔問題

/**  * Title: 漢諾塔問題  * Description:古代有一個梵塔，塔內有三個座A、B、C，A座上有64個盤子，盤子大小不等，大的在下，小的在上。  * 有一個和尚想把這64個盤子從A座移到C座，但每次只能允許移動一個盤子，並且在移動過程中，3個座上的盤子始終保持大盤在下，  * 小盤在上。在移動過程中可以利用B座。要求輸入層數，運算後輸出每步是如何移動的。  *

 * @author rico
 */
public class HanoiTower {

    /**     
     * @description 在程式中，我們把最上面的盤子稱為第一個盤子，把最下面的盤子稱為第N個盤子
     * @author rico       
     * @param level：盤子的個數
     * @param from 盤子的初始地址
     * @param inter 轉移盤子時用於中轉
     * @param to 盤子的目的地址
     */
    public static void moveDish(int level, char from, char inter, char to) {

        if (level == 1) { // 遞迴終止條件
            System.out.println("從" + from + " 移動盤子" + level + " 號到" + to);
        } else {
            // 遞迴呼叫：將level-1個盤子從from移到inter(不是一次性移動，每次只能移動一個盤子,其中to用於週轉)
            moveDish(level - 1, from, to, inter); // 遞迴呼叫，縮小問題的規模
            // 將第level個盤子從A座移到C座
            System.out.println("從" + from + " 移動盤子" + level + " 號到" + to); 
            // 遞迴呼叫：將level-1個盤子從inter移到to,from 用於週轉
            moveDish(level - 1, inter, from, to); // 遞迴呼叫，縮小問題的規模
        }
    }

    public static void main(String[] args) {
        int nDisks = 30;
        moveDish(nDisks, 'A', 'B', 'C');
    }

1. 第三類問題：資料的結構是按遞迴定義的

(1). 二叉樹深度

/**  * Title: 遞迴求解二叉樹的深度  * Description:  * @author rico  * @created 2017年5月8日 下午6:34:50  */

public class BinaryTreeDepth {

    /**     
     * @description 返回二叉數的深度
     * @author rico       
     * @param t
     * @return     
     */
    public static int getTreeDepth(Tree t) {

        // 樹為空
        if (t == null) // 遞迴終止條件
            return 0;

        int left = getTreeDepth(t.left); // 遞迴求左子樹深度，縮小問題的規模
        int right = getTreeDepth(t.left); // 遞迴求右子樹深度，縮小問題的規模

        return left > right ? left + 1 : right + 1;
    }
}

(2). 二叉樹深度

/**
 * @description 前序遍歷(遞迴)
 * @author rico
 * @created 2017年5月22日 下午3:06:11
 * @param root
 * @return
 */

 public String preOrder(Node<E> root) {
        StringBuilder sb = new StringBuilder(); // 存到遞迴呼叫棧
        if (root == null) {   // 遞迴終止條件
            return "";     // ji 
        }else { // 遞迴終止條件
            sb.append(root.data + " "); // 前序遍歷當前結點
            sb.append(preOrder(root.left)); // 前序遍歷左子樹
            sb.append(preOrder(root.right)); // 前序遍歷右子樹
            return sb.toString();
        }       
    }