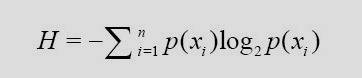簡介

決策樹, 舉兩個栗子:

• 網路上各種心理測試的題, 根據你選的答案, 跳到另一題, 最後得出你是什麼性格的人.
• 圖靈測試, 通過設計各種問題來問跟你聊天的人, 在20 個問題以內, 你來判斷跟你聊天的是機器人還是人.

以上, 都是決策樹的一種形式, 看圖就懂:

• 判斷年齡,->判斷性別->是誰

從根節點, 一步一步判斷(決策過程), 走到葉子節點得到一個確定的分類

• 也可以說是通過一步一步獲取更多資訊 來不斷降低事件的不確定性(資訊熵)

資訊熵

理解:

物理的熵: 判斷空間的混亂程度, 越混亂, 熵值越大 資訊熵: 用來衡量事務的不確定性, 事務越不確定, 熵值越大; 隨機變數不確定性的度量. 計算公式:

• xi 為最後分類的類別
• p(xi) 為: 第 i 個類別出現的次數 / 總次數
• 其中log 與 - 號實際意義不大

決策樹的優劣

• 優點:
  1. 複雜度不高, 結果易理解
  2. 過程直觀
  3. 只需要一次訓練, 儲存在磁碟可之後多次使用
• 缺點:
  1. 可能產生過度匹配(過擬合)問題
• 使用資料：標稱資料或數值資料型別

主要問題

• 如何更快的得到最後的分類結果, 即如何使決策樹的層數最少?
• 更進一步闡述問題: 1. 決策樹主要需要解決的問題: 每一個節點的選擇, 即: 選擇什麼問題來使你獲得更多的資訊, 更有效的降低事物的熵. 2. 如何去掉不必要的分支, 使決策樹更小, 即剪枝

解決方案

• ID3演算法 資訊增益
• C4.5演算法 資訊增益率
• CART演算法 基尼係數

(在此, 我主要討論ID3演算法, 並且只討論如何選擇節點, 不管剪枝問題, 待更新…)

ID3演算法

簡介

• id3演算法採用資訊增益來選擇節點
• 資訊增益: 假如當前需分類事務的熵為 0.9, 在得到一個資訊後(向下經過一個節點之後), 再次計算此時的熵為 0.4, 那麼, 選擇該節點的資訊增益為 0.9-0.6 = 0.4
• 只能用標稱型資料, 若是數值型需要給資料劃分

訓練過程

輸入: 資料特徵及其所屬類別 輸出: 一棵決策樹 此處我們選擇的歸納偏好為: 當只有一個屬性無法劃分, 而存在多個標籤時, 選擇最多的標籤作為最終結果 演算法: 採用遞迴的形式構造, 即從根節點開始, 不斷進入子樹遞迴構造

程式碼:

def create_tree(dataSet, labels):
   classList = [exam[-1] for exam in dataSet]
   # 1. 若所有的類別相同, 到達葉子節點, 停止劃分,
   if classList.count(classList[0]) == len(classList):
       return classList[0]

   # 2. 遍歷完了所有特徵時, 返回出現最多的類別
   if len(dataSet) == 1:
       return major_class(classList) // 根據歸納偏好設定葉子節點標籤

   # 建立一個新的分支
   split_feature = get_best_split_feature(dataSet)
   split_feature_label = labels[split_feature]
   mytree = {split_feature_label:{}}
   del(labels[split_feature])  # 去除當前子標籤族的split_feature的標籤
   feat_values = set([exam[split_feature] for exam in dataSet])
   for value in feat_values:
       sublabels = labels[:]
       mytree[split_feature_label][value] = create_tree(split_dataset(dataSet, split_feature, >value), sublabels)
   return mytree

資訊熵的計算

由公式可知, 資訊熵的計算就是訓練資料中所有標籤出現的概率求和 dataSet: 訓練集 返回 ent 夏農熵 calc_shannooEnt: 程式碼:

def calc_shannonEnt(dataSet):
   """
   計算夏農熵
   :param dataSet: 資料集: 格式: 列表  [ [值,值,值, ...],
                                         [值,值,值, ...],
                                         [值,值,值, ...],
                                         ...   ]
   :return: 每一種可能分類的資訊熵
   """
   shannonEnt = 0.0
   data_num = len(dataSet)
   # 給最後一個屬性的值的種類當作分類
   label = {}  # key:可能的分類, v: 分類的個數
   for features in dataSet:
       if features[-1] not in label.keys():
           label[features[-1]] = 0
       label[features[-1]] += 1
   # 計算夏農熵公式:
   for key in label:
       prob = float(label[key]) / data_num
       shannonEnt -= prob * log2(prob)
   return shannonEnt

獲取最好的劃分特徵

• 資訊增益的計算公式 Dv為以屬性v劃分D後的資料集 |D|為資料集的樣本數量
• 演算法

1. 計算當前初始資料集的資訊熵 base_ent
2. 遍歷當前特徵族
   • 按照每個特徵來劃分資料集得到sub_dataset
   • 計算每個sub_dataset的資訊熵new_ent, 並記錄對應的劃分的特徵
   • 該劃分的計算資訊增益, base_ent - new_int
   • 獲取最大的資訊增益
3. 返回得到最大資訊增益劃分特徵

程式碼:

def get_best_split_feature(dataSet):
   # 因為最後一個屬性是分類結果, 所以要 -1
   num_features = len(dataSet[0]) - 1
   base_ent = calc_shannonEnt(dataSet)
   best_info_gain = 0.0
   split_feature = -1
   for i in range(num_features):
       i_feature = set([exam[i] for exam in dataSet]) # 獲取第i個屬性的所有取值
       new_entropy = 0.0
       # 計算按第i個屬性劃分的資訊增益
       for value in i_feature:
           sub_dataSet = split_dataset(dataSet, i, value)
           prob = len(sub_dataSet) / float(len(dataSet))
           new_entropy = prob * calc_shannonEnt(sub_dataSet)
       info_gain = base_ent - new_entropy

       if info_gain > best_info_gain:
           best_info_gain = info_gain
           split_feature = i
   return split_feature

根據 feature 與 value 劃分資料集

1. 遍歷dataset中的 所有樣例
2. 樣例的 feature == value 新增到結果集中, 並去掉該樣例的這個 feature

程式碼:

def split_dataset(dataSet, axis, value):
   """
   按照axis=value來劃分資料集為
   :param dataSet:
   :param axis: int 劃分資料集的featrues
   :param value:
   :return: 按照value劃分後的資料集, 並去掉該axis特徵(屬性)
   """
   split_res = []
   for features in dataSet:
       # 獲取去掉該axis特徵的結果
       if features[axis] == value:
           axis_after = features[axis + 1:]
           extend = features[0:axis]
           extend.extend(axis_after)
           split_res.append(extend)
   return split_res

ID3演算法的缺點與資訊增益率:

• 想象: 若給資料集中每個資料一個id, 大家知道 id 是一個無意義的值, 但是, 我們計算器資訊增益時, 根據id劃分的子集中, 只有一個樣本, 而且樣本只屬於一個類別, 那麼公式中, log2(pi) = 0, 所以, 該資訊熵為0; id的資訊增益為base_ent - 0, 最大!
• 所以, 根據資訊增益得到的結果, 更偏向於屬性值多的屬性

因此 提出了C4.5演算法, 根據資訊增益率來確定用來劃分的特徵 資訊增益率:

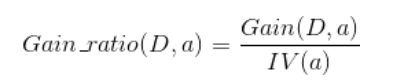
• Gain_ratio(D,a): 以屬性a來劃分資料D的資訊增益率
• Gain(D,a): 以屬性a來劃分資料D的資訊增益
• IV(a): 屬性a的熵, 即 a 這個屬性本身的純度, 值為:

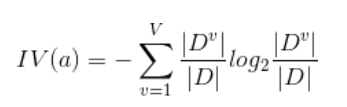
簡單說 資訊增益率為: 用 (以屬性v劃分的資訊增益 )gain(D,x) / ent(x) (屬性x的資訊熵)

我們用資訊增益率來計算剛剛的極端情況下 ID 的那個例子: 得到的gain(D,x)最大, 而 log2(|Dv| / |D|)為0, 所以 ent(x)取0, 所以 資訊增益率為正無窮. 問題解決

未完待續