決策樹分類是資料探勘中分類分析的一種演算法。顧名思義，決策樹是基於“樹”結構來進行決策的，是人類在面臨決策問題時一種很自然的處理機制。例如下圖一個簡單的判別買不買電腦的決策樹：

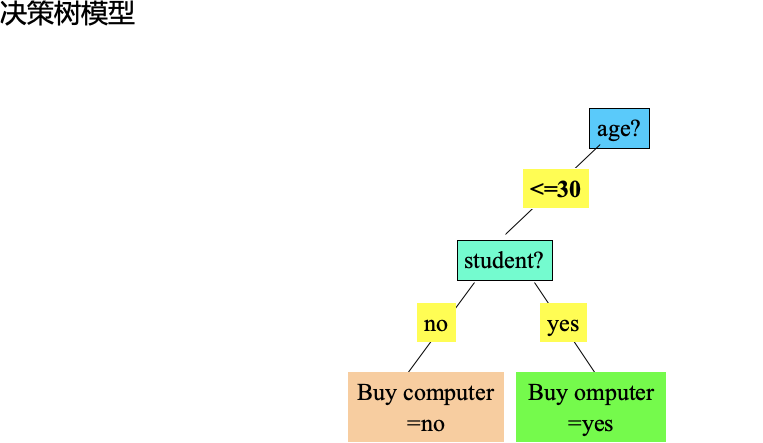
 下圖是一個測試資料集，我們以此資料集為例，來看下如何生成一棵決策樹。

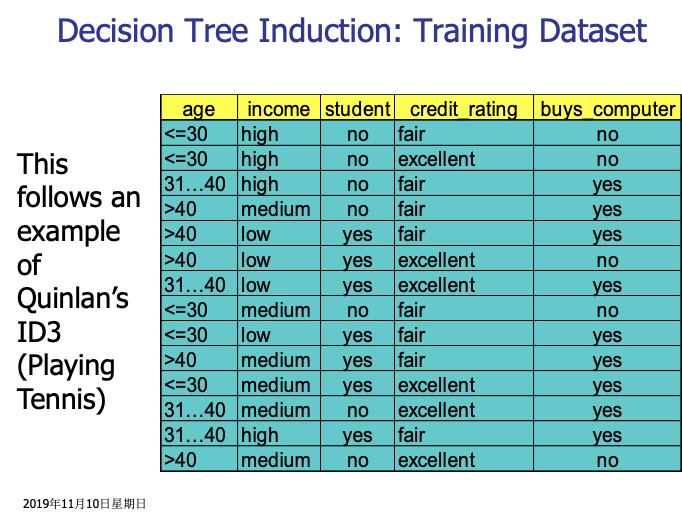
 決策樹分類的主要任務是要確定各個類別的決策區域，或者說，確定不同類別之間的邊界。在決策樹分類模型中，不同類別之間的邊界通過一個樹狀結構來表示。

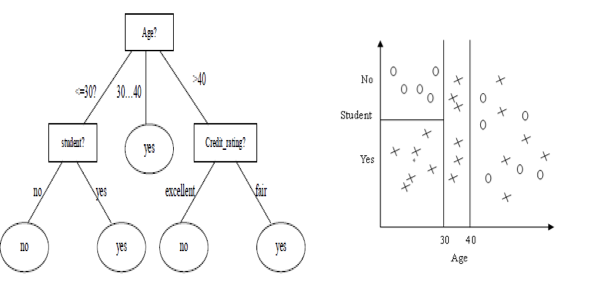
 通過以上分析，我們可以得出以下幾點：

• 最大高度=決策屬性的個數
• 樹越矮越好
• 要把重要的、好的屬性放在樹根

因此，決策樹建樹演算法就是：選擇樹根的過程

 第一步，選擇屬性作為樹根

比較流行的屬性選擇方法：資訊增益

資訊增益最大的屬性被認為是最好的樹根

在選擇屬性之前，我們先來了解一個概念：熵 什麼是熵？什麼是資訊？如何度量他們？

下面這個文章通俗易懂的解釋了這個概念

http://www.360doc.com/content/19/0610/07/39482793_841453815.shtml

熵用來表示不確定性的大小

資訊用來消除不確定性

實際上，給定訓練集S，資訊增益代表的是在不考慮任何輸入變數的情況下確定S中任一樣本所屬類別需要的資訊（以消除不確定性）與考慮了某一輸入變數X後確定S中任一樣本所屬類別需要的資訊之間的差。差越大，說明引入輸入變數X後，消除的不確定性，該變數對分類所起的作用就越大，因此被稱為是好的分裂變數。換句話說，要確定S中任一樣本所屬類別，我們希望所需要的資訊越少越好，而引入輸入變數X能夠減少分類所需要的資訊，因此說輸入變數X為分類這個資料探勘任務帶來了資訊增益。資訊增益越大，說明輸入變數X越重要，因此應該被認為是好的分裂變數而優先選擇。

因此，計算資訊增益的總的思路是：

1) 首先計算不考慮任何輸入變數的情況下要確定S中任一樣本所屬類別需要的熵Entropy(S)；

2) 計算引入每個輸入變數X後要確定S中任一樣本所屬類別需要的熵Entropy (X,S);

3) 計算二者的差，Entropy (S) - Entropy (X, S)，此即為變數X所能帶來的資訊（增益），記為Gain(X,S)。

結合上面對於熵的解釋的文章裡，我們能得出求熵的公式：

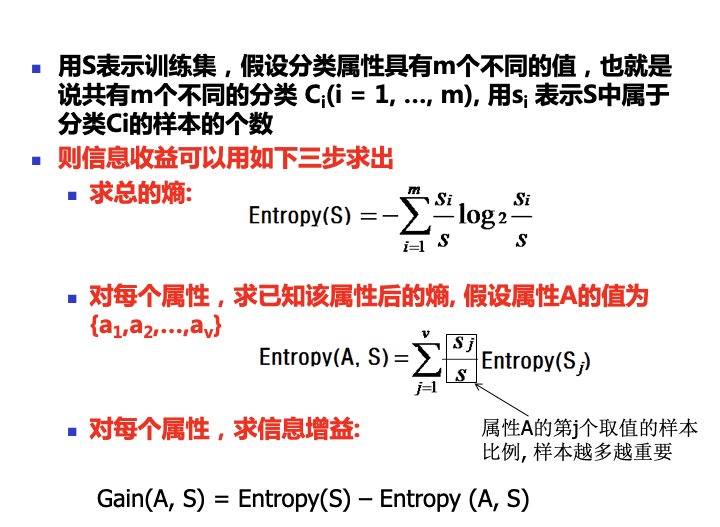
 下圖很形象的解釋了熵代表的含義。

 我們還以上面的一組資料來分析，資訊增益具體應該怎麼算

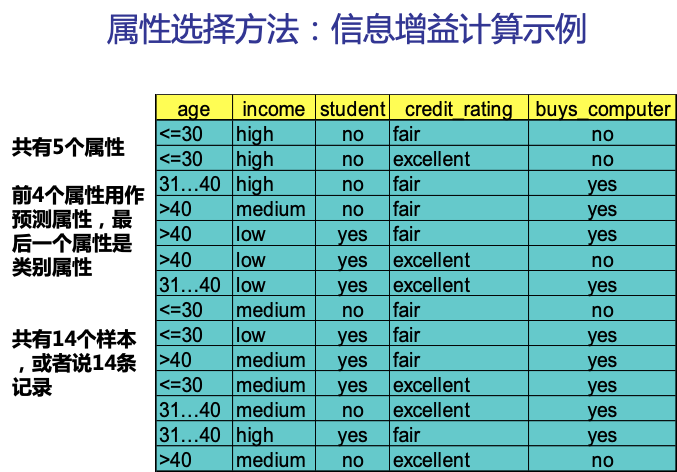
 根據上面的討論，我們先用公式計算不考慮任何輸入屬性時，要確定訓練集S中任一樣本所屬類別需要的熵。

此例子中，目標屬性即buys_computer，有2個不同的取值，yes和no，因此有2個不同的類別（m=2）。設P對應buys_computer=yes的情況，N對應buys_computer=no的情況，則P有9個樣本，N有5個樣本。所以，總的熵就是：

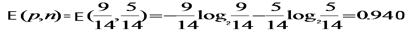
 即，E(p,n) = E(9,5) = 0.940

然後我們來求屬性age的熵，age有三個屬性，樣本個數分別為5，4，5，所以屬性age的熵就是：

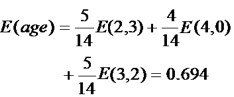
 最後，我們可以求出屬性age的資訊增益為：

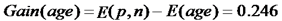
 同樣的，我們可以分別求出income，student和credit_rating的資訊增益

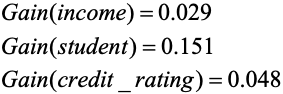
 finally，我們可以得出屬性age的資訊增益最大，所以，應該用屬性age作為樹根。

確定好樹根之後，下一步我們還要按照剛才的步驟來確定下一個節點的左右子樹分別用哪個屬性作為樹根，直到最後得出完整的決策樹。

雖然決策樹分類演算法可以快速的預測分類，但是也會有過度擬合（Overfitting）的問題。

有些生成的決策樹完全服從於訓練集，太循規蹈矩，以至於生成了太多的分支，某些分支可能是一些特殊情況，出現的次數很少，不具有代表性，更有甚者僅在訓練集中出現，導致模型的準確性很低。

通常採用剪枝的方式來克服 overfitting，剪枝有兩種方法：

先剪:構造樹的過程中進行修剪。不符合條件的分支則不建。

後剪: 整個樹生成之後進行修剪

&n