Abstract: This paper aims to clearly interpret the process of Hill’s cipher and the mathematical method in it, also we will sequentially focus on the deeper use of Hill’s cipher as well as applications, and eventually deduce the procedure with the help of Matlab.

Key Words: Hill cipher, Cryptography, inverse of the matrix, decryption, encryption, image encryption.

1. Introduction

It’s generally accepted by all that network and electronic commerce have played vital role in nowadays individuals daily life due to the rapid development of computer technology and modern times communication technique. Digitization as well as informatization are tend to be the trend and flourish of future technology development.

However, with the widely use of Internet, some crimes and frauds are conducted by using the leak of information and unsafe security cyber surroundings, so it is of critical significance to pay attention to the information security. According some reference book, we’ve already know that the modern field of cryptography are divided into several areas of study such as symmetric-key cryptography, public-key cryptography as well as some encryption key.

This paper is mainly focus on one type of cryptography named Hill cipher, which is a classical polygraphic substitution cipher based on linear algebra. This kind of cipher was invented by Lester. S. Hill in 1929.We’ll profoundly describe the theory of the Hill cipher by using some basic knowledge of elementary matrices (inverse matrices), and with the help of MATLAB and using some examples to introduce the further use of Hill cipher as well as other different kinds of way of cryptograph.

2. Section 2

2.1

The basic method of Hill cipher is using a key matrix to multiply a plaintext vector in order to get a ciphertext vector and change it into the string of ciphertext. The key matrix is actually a transformation matrix. We suppose the plaintext vector is

 P=  with 26 characters changed into numbers by using the ASCII（American Standard Code for Information Interchange）,while the key matrix is a n*n matric matrix K=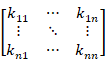  .Also suppose the ciphertext vector is C= , then use the equation:

 to get the ciphertext vector:

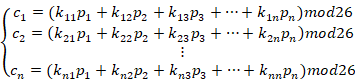
And we will decrypt the cipher by using the inverse of the matrix like:

In which                       (I has to be an identity matrix)

2.2

In order to profoundly explain the procedure of decryption as well as encryption, we take a convincing example to illustrate the process of Hill’s cipher.

Encryption

1)We transform Chinese character into Chinese phonetic alphabet as a Plaintext:

    Example:

    you nei gui

    Divide the plaintext into n-letter groups (n is determined by the key)

    you nei gui

2)Each plaintext letter is assigned a numerical value from 0 to 25, similarly as in the Caesar cipher from a to z.

a	b	c	d	e	f	g	h	i	j	k	l	m
0	1	2	3	4	5	6	7	8	9	10	11	12
n	o	p	q	r	s	t	u	v	w	x	y	z
13	14	15	16	17	18	19	20	21	22	23	24	25

Plaintext:  y    o    u     n   e   i   g   u    i

                24  14  20 , 13  4  8 , 6  20  8

3)Fill the plaintext values into the P matrix

  (from peak to bottom, from left to right)

4)Use the encryption algorithm: (Point: The matrix multiplication is not commutative KP and PK are not equal in general)

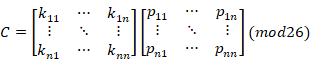
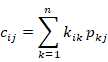
In this case, we set the key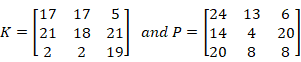

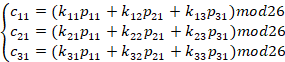
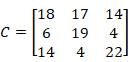
Which use the Caesar list to transform it and result in sgo rte oew

Decryption

1. The process of decryption involves the inverse of the matrix

1. So, the key factor to get P is to calculate

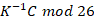
Before we start to do calculation, we shall check the Modular Arithmetic

Which means

                   

                   

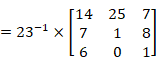
At this step we should apply Modular Multiplicative Inverse

There exist

Which  

(** Not every integer a has a multiplication inverse, it exists if and only if a and m are coprime)

The modular multiplicative inverse of x modulo y can be found with the extended Euclid algorithm if

Then

a	1	3	5	7	9	11	15	17	19	21	23	25
a-1 mod 26	1	9	21	15	3	19	7	23	11	5	17	25

So

                   

                   

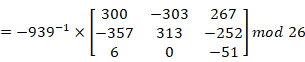
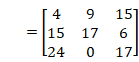
Then we apply this into

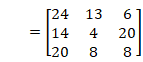
1. Then we transform the value into characters and result in the ciphertext:

you nei gui

3. Section 3

This part introduces a general process applying Hill cipher in image encryption, whose main purpose is covering the information contained in the image,

Matrix Model

• 2×2 matrix model

Every pixel in a image is formed by three kinds of RGB color value(R-Red, G-Green, B-Blue). And each value will be expressed as a integer from 0 to 255 in computer. Because of that, we can put RGB values of each pixel with another value to constitute a 2×2 matrix whose elements are the values above. It can be expressed like  and the sequence of  can be an arbitrary sequence of . (The arrangement can also be a part of the “plaintext”)

*The options of  are various. But it must satisfy the condition of being a integer from 0 to 255, which can be the digital signature, the random numbers or even a constant.

• 3×1 matrix model

We can just simply put three RGB values into a 3×1 matrix like  (the sequence of  can be an arbitrary sequence of Rij,Gij,Bij sequence of  and the arrangement can also be a part of the “plaintext”).

Logistic Map

Logistic map is a kind of dynamic system which is widely studied. The definition of it is

Xn+1= λXn(1-Xn), n=0,1,2…

As a phenomenon found in non-linear dynamic system, chaos is a deterministic and random-like process. Researches shows that when parameter λ∈(3.5699456,4), logistic map is at chaos state. Therefore, the resulting chaotic sequence is suited for generating encryption sequence.

Encryption

Ⅰ. Determine the matrix size and arrangement of elements

• 2×2 matrix model

Let

=,∈∩Z

, then

=1

(1 is a coprime factor of 256).

For convenience, let

==(mod256)=

, and the , ,  are the new RGB values of every pixel.

• 3×1 matrix model

Let

, ,∈∩Z, ≠

(otherwise the matrix will not be invertible)

, then

=()

(( ) and ( )must be coprime factors of 256).

For convenience, let

=, = =(mod256)=

.(and the , ,  are the new RGB values of every pixel).

II. Generate encrypting matrices

Setup parameter λ∈(3.5699456,4) and initial value ∈[0,1] for the guarantee of ∈[0,1], then a chaotic sequence is got. Let

=[255]

([x] is the rounding function, x-1<[x]≤x),

=2[127]+1&=2[128]

(to satisfy that () and () are coprime factors of 256)

III. Compute

       Using formula compute every pixel’s color after encryption.

Decryption

I. Confirm the secret key

Confirm all the information for decryption included the arrangement of pixel matrix, λ and .

II. Generate Decryption matrices and Compute

For 2×2 encryption matrices, use formula

==mod256=mod256

(The =1 and the modular multiplicative inverse of 1 modulo 256 is also 1.)

to restore the original image.

While for 3×3 encryption matrices, use following formulas.

(+,+)mod256

=()+()+()mod256

=()(++)mod256=()mod256

( , and  is the only solution due to  is a coprime factor of 256)

(-)mod256=()mod256

(  is the only solution due to  is a coprime factor of 256, as well as  and )

(a).Original image

  

(b). 2×2 matrix encrypted image        (c). 3×1 matrix encrypted image

  

(d). 2×2 matrix decrypted image       (e). 3×1 matrix decrypted image

4. Section 4

This part provides two sample MATLAB codes for encryption and decryption respectively.

NB the program runs on Capitalized information and only transfer letter in the unit of a certain length of combination which depends on the dimension of key matrix.

PART I Encryption

function hill()

%Enter key

disp('Enter the dimension of the key matrix');

n=input('');

disp('Enter the key matrix in the order of rows');

key=zeros(n,n);

for j=1:n;

    for k=1:n

        key(j,k)=input('');

    end

end

d=det(key);%Determinant

if d==0

   error('Not invertible.Cant hill');

end

%Enter info

message=input('Enter the inf in CAPITALS \n','s');

m=size(message);

m=m(2);%Get length

if mod(m,n)~=0

    error('Error.Entering code should be multiplier of the key matrix dimension');

end

for i=1:m

    if message(i)>='A' && message (i)<='Z' 

        message(i)=message(i)-65;

    else

        error('Error. Captial letters are needed.');

    end

end

%Encryption

i=1;

while i<m+1

    B=message(i:i+n-1)';

    a=key*B;

    A(i:i+n-1)=a';

    i=i+n;

end

for i=1:m

    if A(i)>26

        A(i)=mod(A(i),26);

    end

    A(i)=A(i)+65;

end

str=char(A);

fprintf('The code is %s',str)

end

PART II Decryption

%Decryption

function hill2()

%Enter key

disp('Enter the dimension of the key matrix');

n=input('');

disp('Enter the key matrix in the order of rows');

key=zeros(n,n);

for j=1:n

    for k=1:n

        key(j,k)=input('');

    end

end

d=det(key);%Determinant

if d==0

    error('Not invertible.Cant hill');

end

%ÊäÈëÃÜÎÄ

message=input('Enter the code\n','s');

m=size(message);

m=m(2);

if mod(m,n) ~=0

    error ('Error.Entering code should be multiplier of the key matrix dimension');

end

for i=1:m

    if message(i)>='A'&& message(i)<='Z'

        message(i)=message(i)-65;

    else

        error('Error. Captial letters are needed.');

    end

end

%r1 is the modular multiplicative inverse of d

while abs(d)>26

    d=mod(d,26);

end

switch d

    case 1

        r1=1;

    case 3

        r1=9;

    case 5

        r1=21;

    case 7

        r1=15;

    case 9

        r1=3;

    case 11

        r1=19;

    case 15

        r1=7;

    case 17

        r1=23;

    case 19

        r1=11;

    case 21

        r1=5

    case 23

        r1=17

    case 25

        r1=25;

    otherwise disp('The reciprocal of d doesnt exist');

end

detk=det(key);

invk=inv(key);

k=detk*invk;

key2=mod(r1*k,26);

for i=1:n

    for j=1:n

        if key2(i,j)<0

        key2(i,j)=key2(i,j)+26;

        end

    end

end

i=1;

while i<m+1

    p= message(i:i+n-1)';

    a=key2*p;

    B(i:i+n-1)=a';

    i=i+n;

end

for i=1:m

    if B(i)>26

        B(i)=mod(B(i),26);

    end

    if B(i)==0

        B(i)=26;

    end

    B(i)=B(i)+65;

end

str2=char(B);

fprintf('\nThe inf is %s\n',str2);

end

The command window result screenshots:

                    Figure 1                                     Figure 2

5. Conclusions

This paper meanly illustrate the acute procedures of encryption and decryption of Hill’s cipher by applying the knowledge of inverse of matrix and modular arithmetic. Additionally, it shows the deeper use of Hill’s cipher on image, text and other applications which plays an essential part in nowadays network security and electronic commerce even in the military fields.

References

1. Xu Xiao-hua and Li Min-ying(2010), The Solution of Matrix of Hill Cipher in Encryption and Decryption.
2. Ahmed Y. Mahmoud, Alexander G. Chefranov(2014), A Hill Cipher Modification Based on Eigenvalues Extension with Dynamic Key Size HCM-EXDKS.
3. Liu jiwei(2010), Digital image encryption algorithm based on hill cipher.