Introduction to determinants

Determinants is a unique concept that memorizing the formula is rather simple, but understanding its meaning and true potential is often more challenging. In short, “determinant” is the scale factor for the area or volume represented by the column vectors in a square matrix. To understand this, I can’t stress enough how important it is to watch this amazing video from 3Blue1Brown.

Make sure to just spend 10 mins watching this video to get general idea on what determinant is.

Now you have a general idea about what the determinant is. Let’s take a look at the formula now.

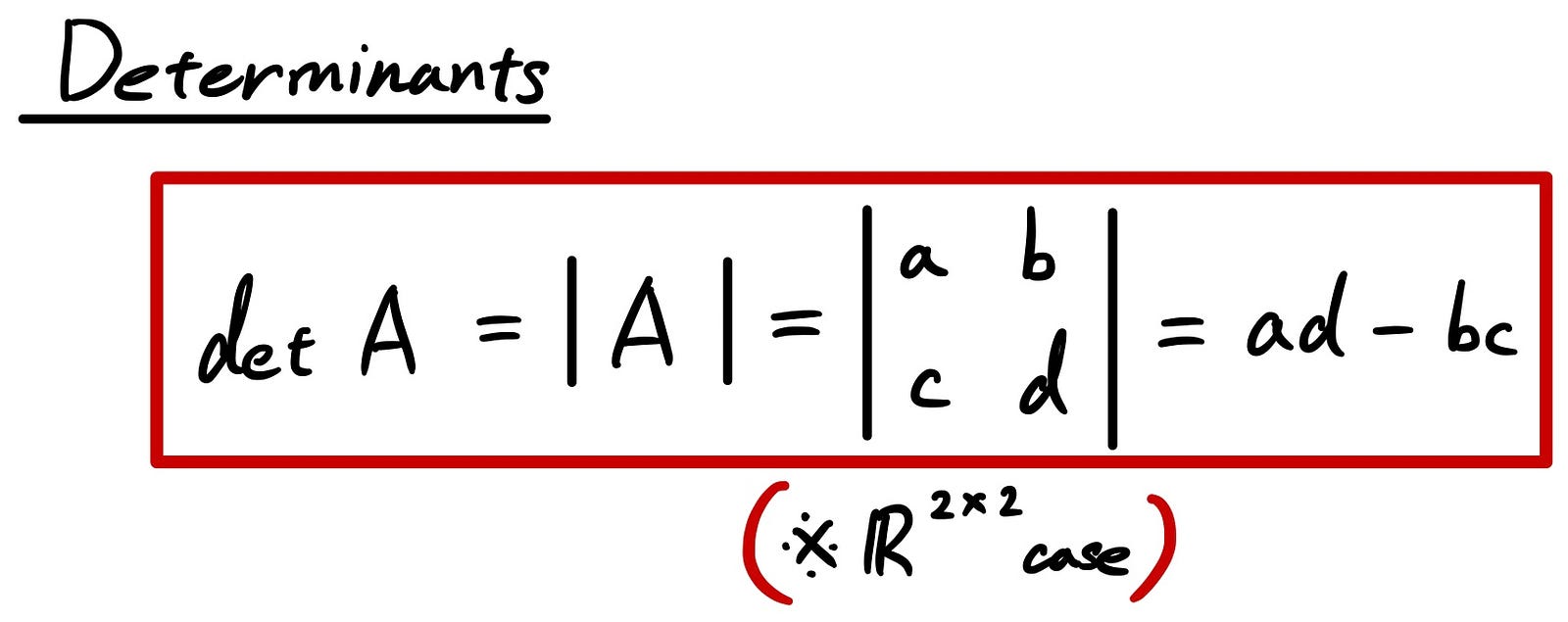
This is the two by two case and the general formula is rather complexing so I’ll just leave it to the wiki page for you to check

Determinants and its properties

This is actually the main topic we want to discuss today. The properties of the determinant.

You can see the complete lecture from Dr.Strang from MIT on this at Lecture 18.

I’m basically summarizing and adding some more information so that it’s easier to understand.

If you watched the 1st video posted on this story, you can understand this first property. If it’s the identity matrix that we are talking about, the column vectors are orthogonal to each other and there’s nothing to scale. That’s why the determinant is always 1.

The 2nd property is that when you exchange any rows, it will flip the sign of the determinant.

If you remember the the video from 3Blue1Brown, you could understand the following example. Basically, by exchanging rows, the arrows flip its positions, thus resulting in changing it’s signs.

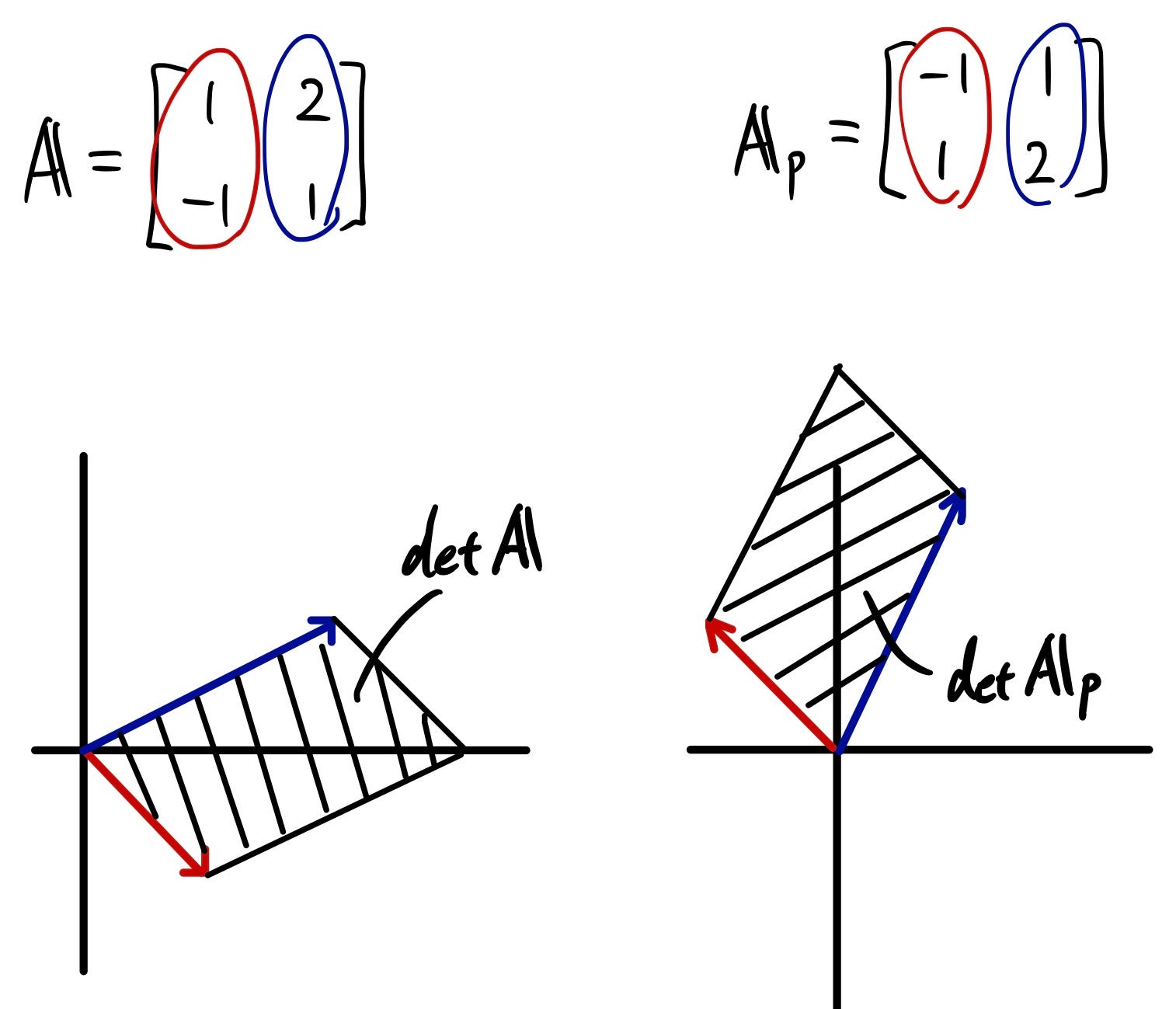
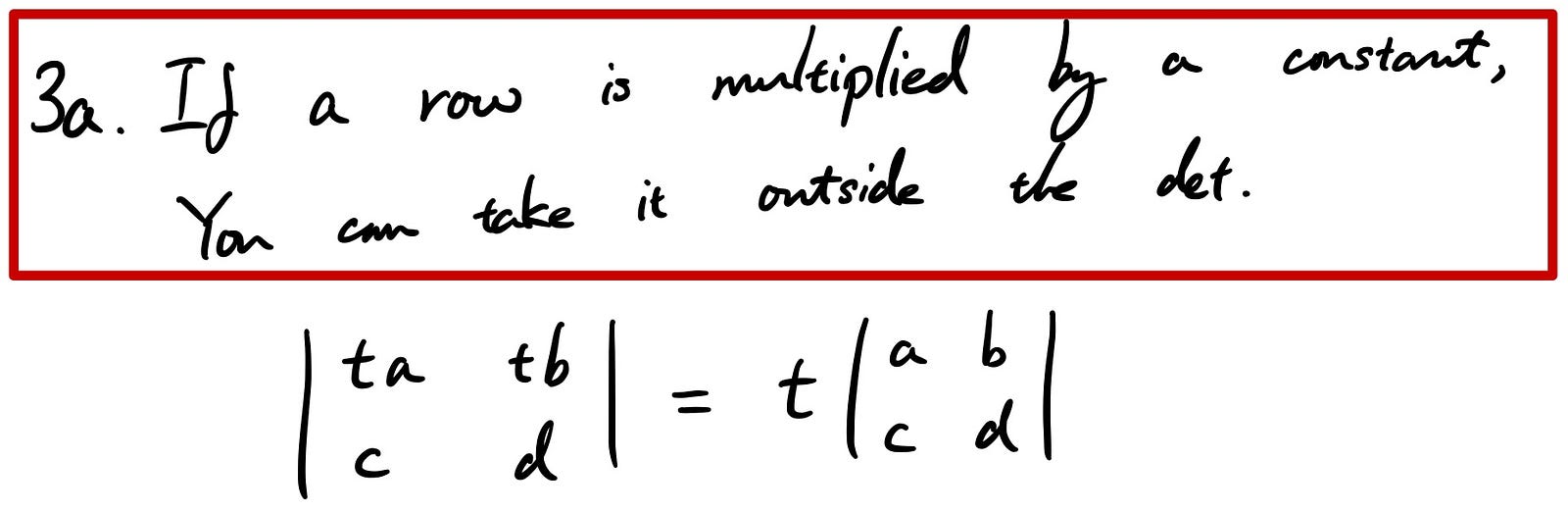
Let’s take an easy example here again.

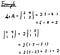
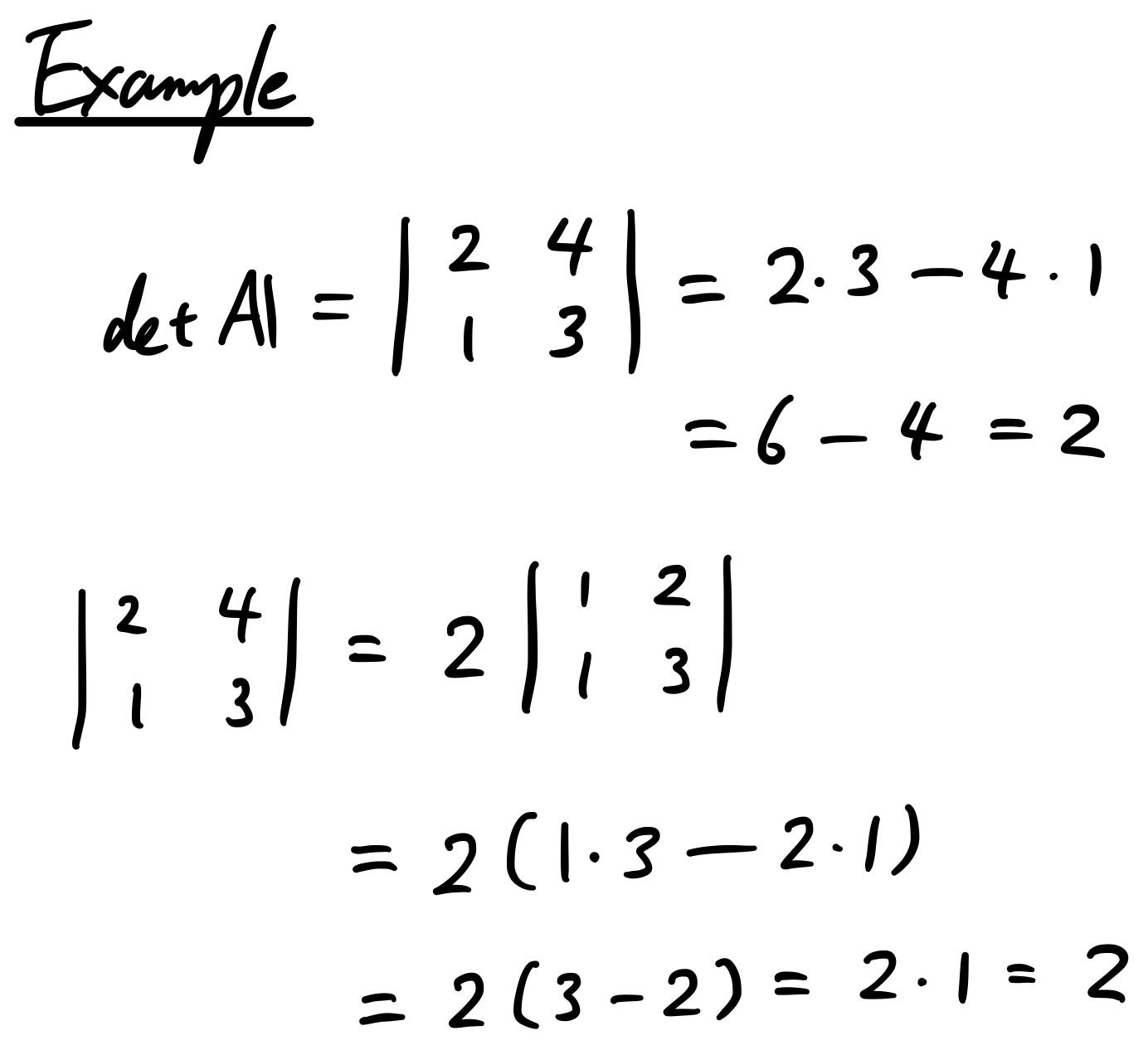
Similar to the above, there’s another property in 3.

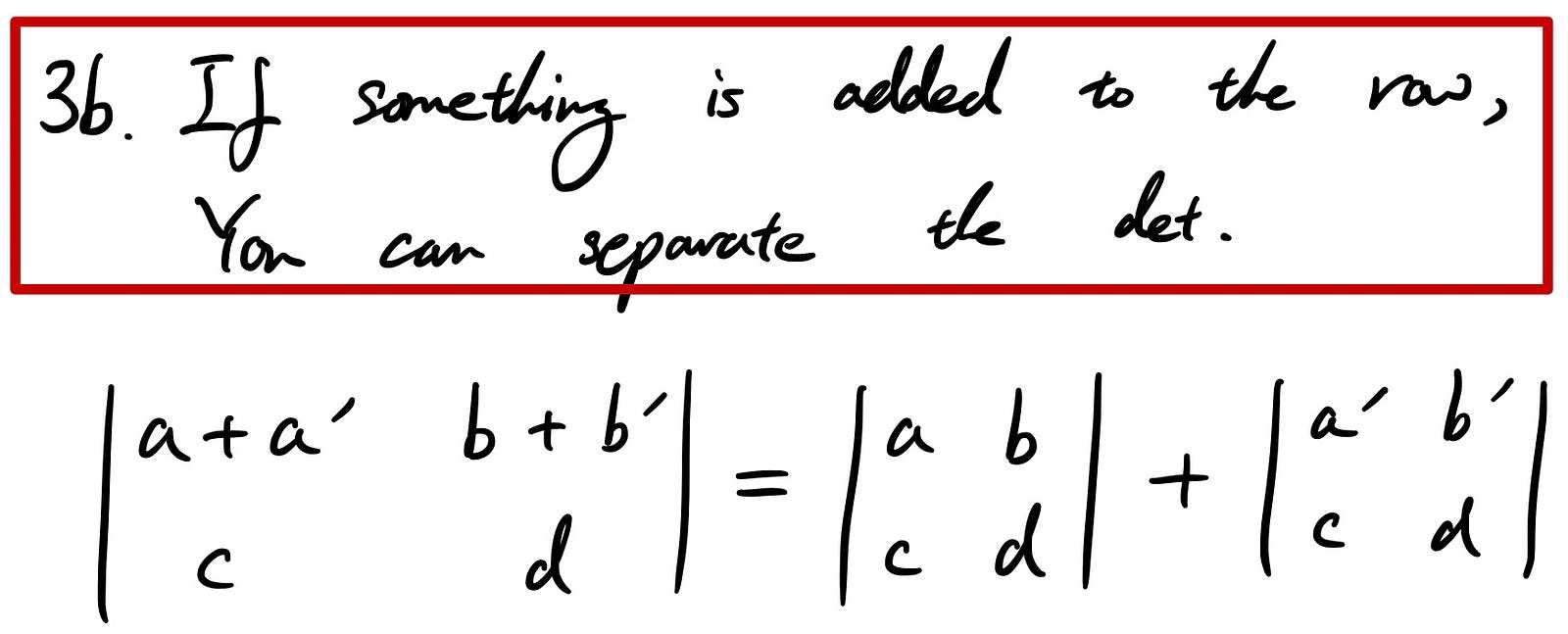
Let’s take another easy example for this property too.

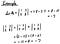
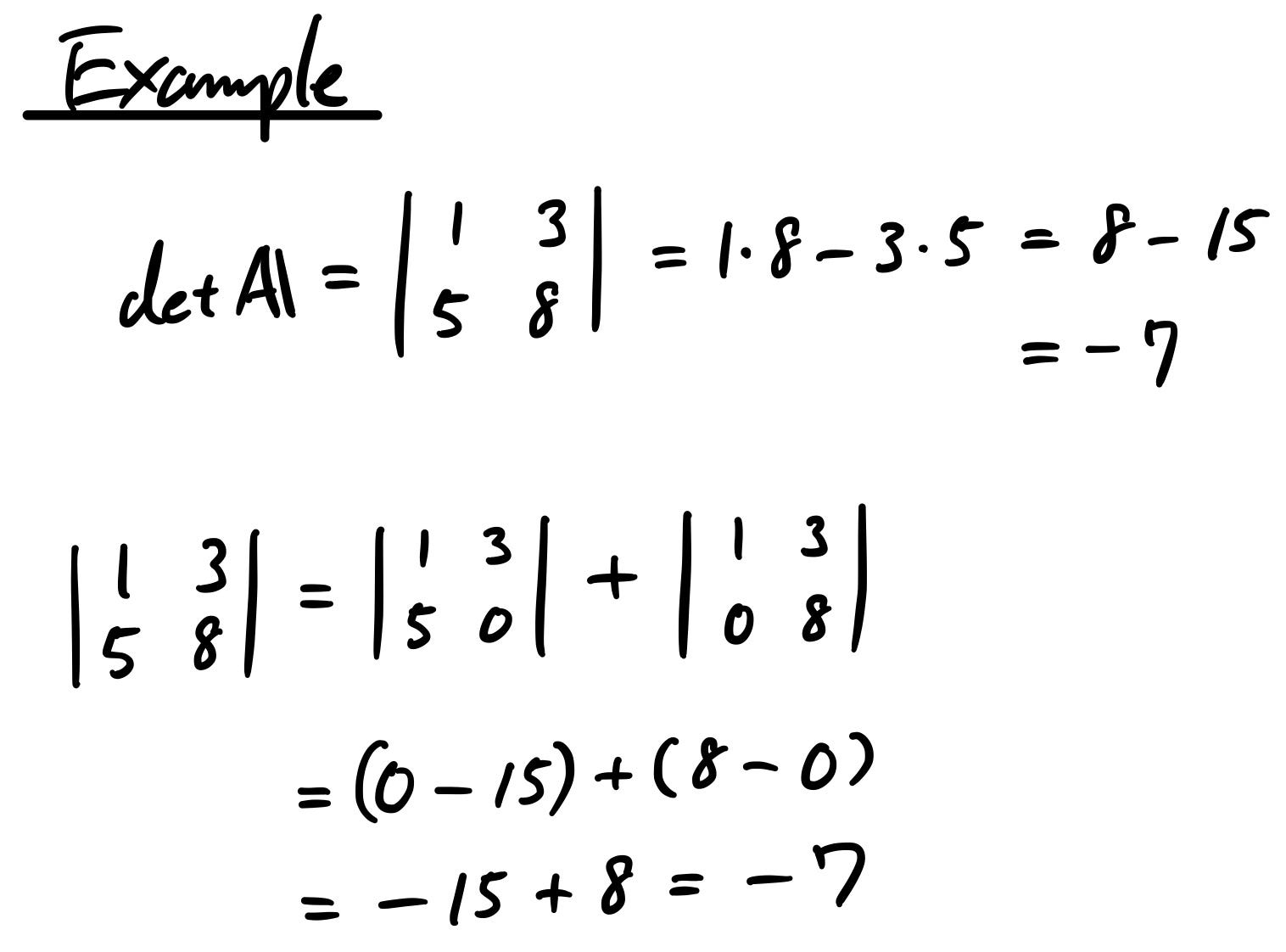
The 4th property can be derived from the 2nd property we already described.

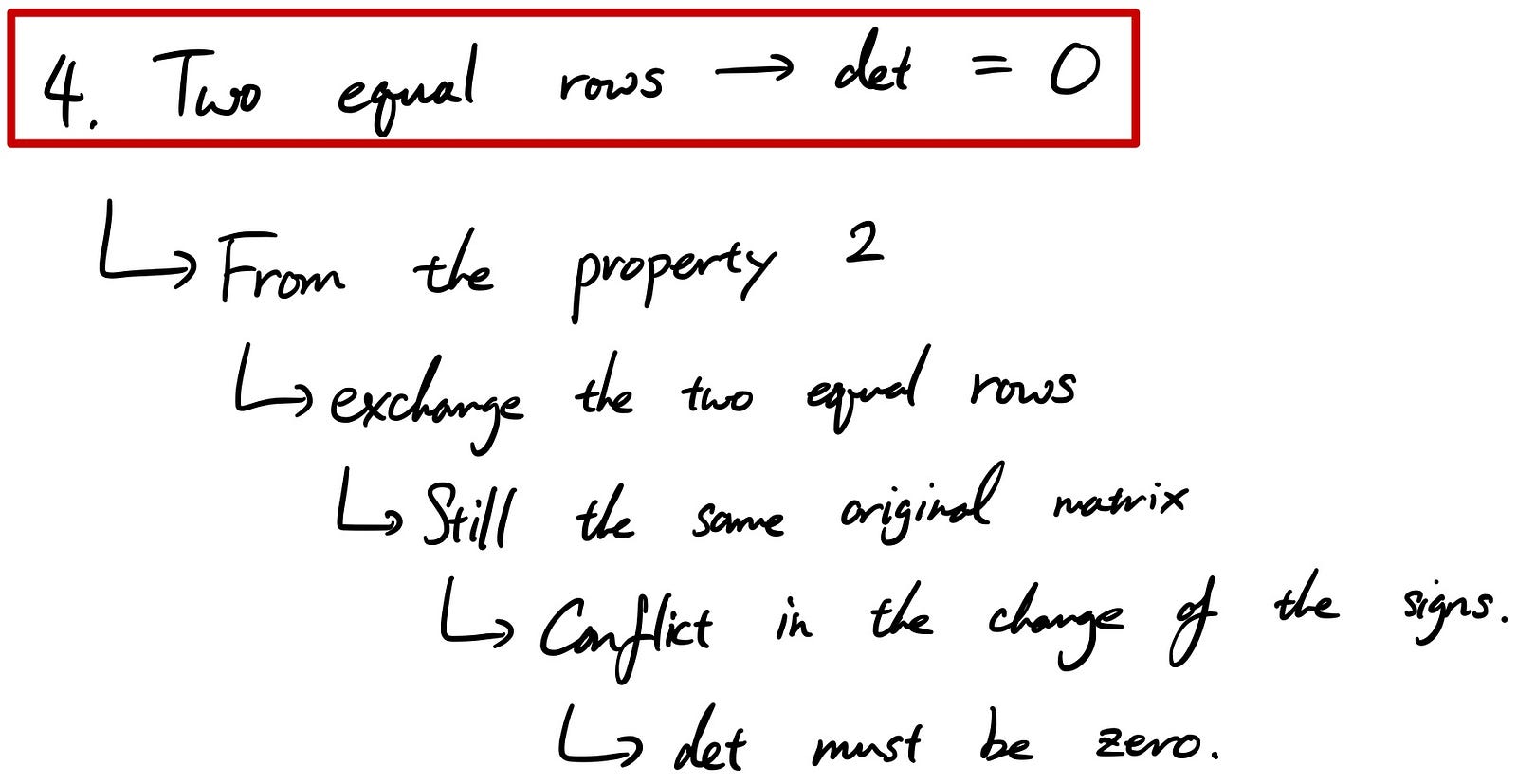
From here, it’s easier to show why using the properties that we already covered. The 5th property can be shown using multiple properties.

Here’s some concrete example.

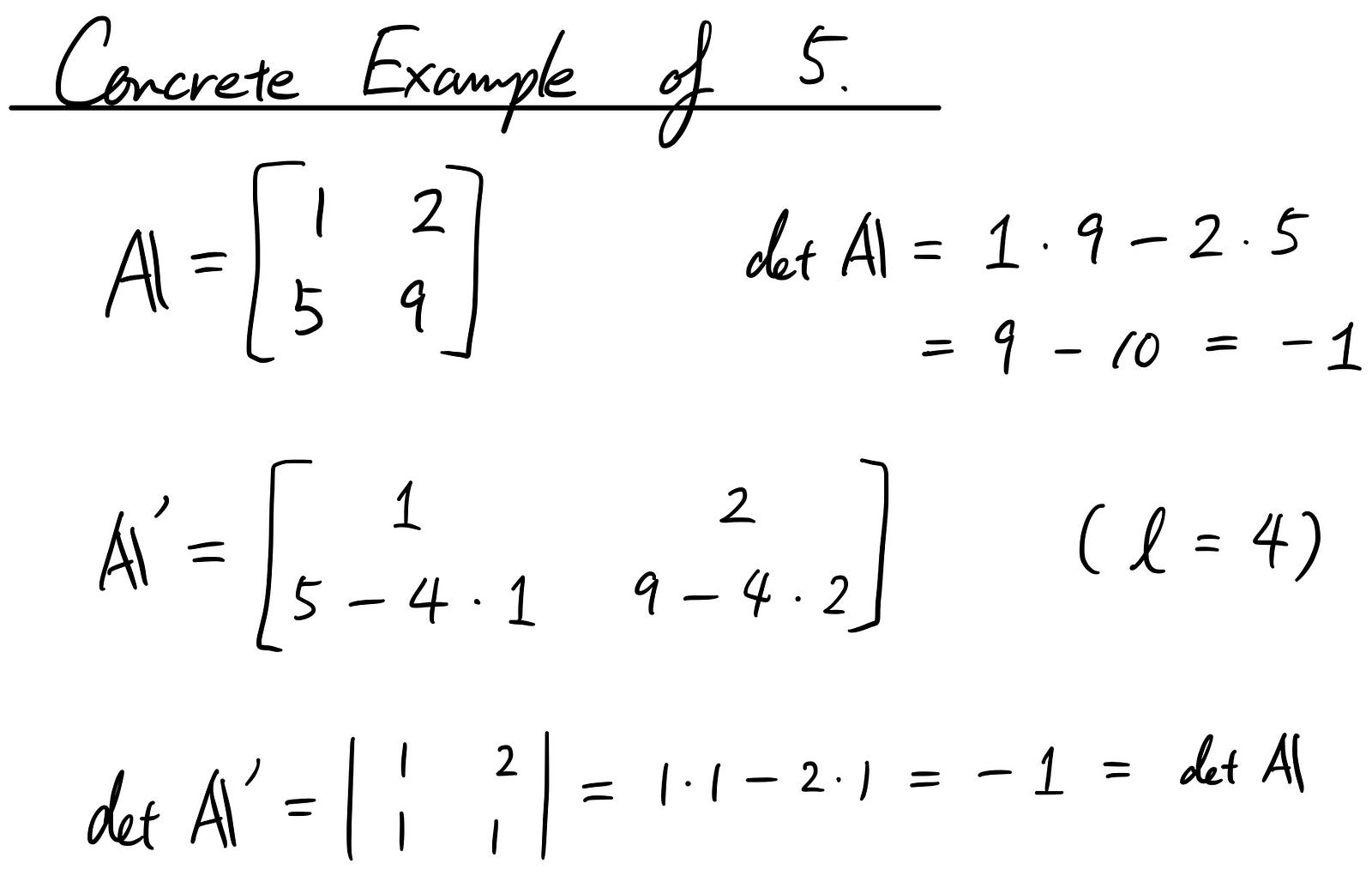
The last three properties are pretty important as it comes back again and again in the later stories.

For example, property 8 is so important because it’s used to check if the matrix is invertible or not.

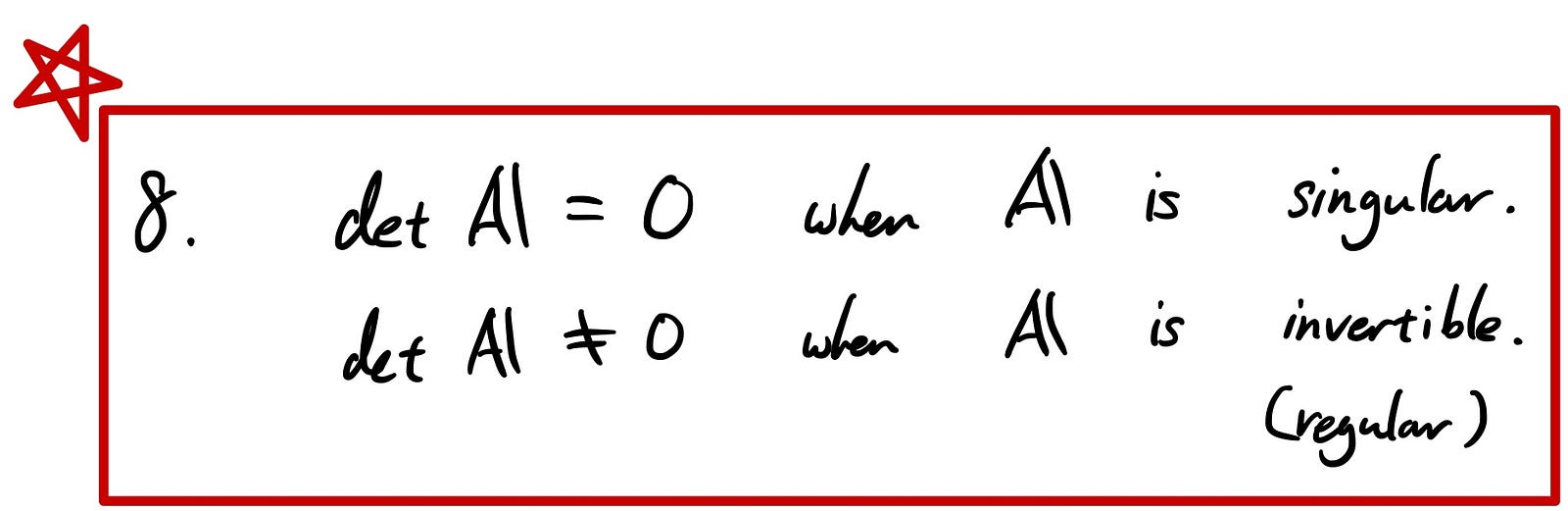
Property 9 comes in handy when it is difficult to calculate some determinants.

Property 10 is good to remember too.

So that’s it for the properties of the determinants. Let’s use these to derive the determinants equation of 2 x 2 case.

Deriving the original formula for determinants 2 x 2 case

First, let’s recap what the formula was.

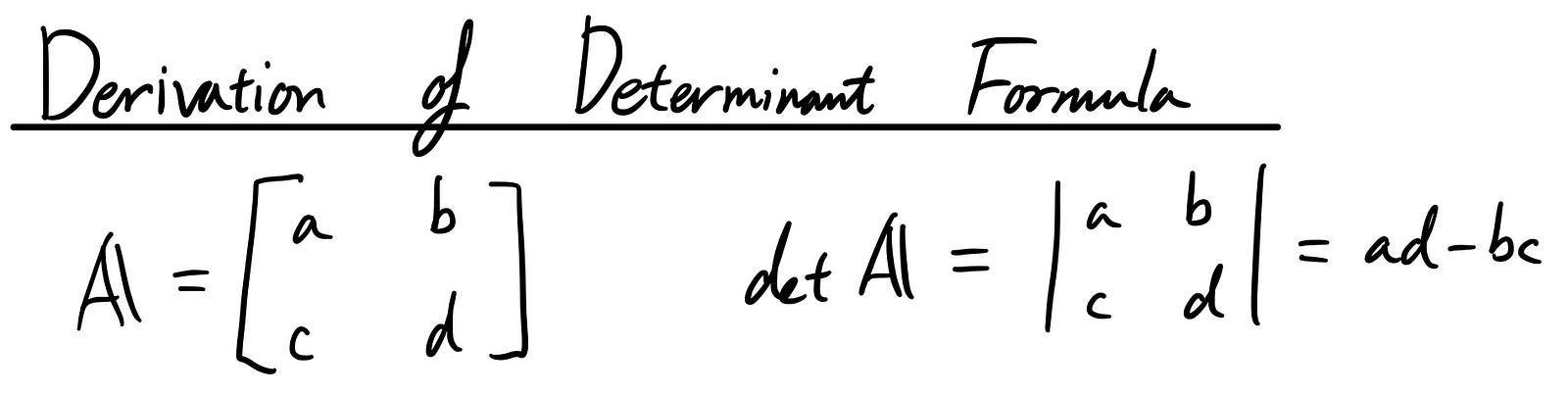
To get this formula, we are going to use quite a lot of the properties that we already discussed.

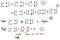
Then restarting from the equation that we just starred…

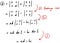
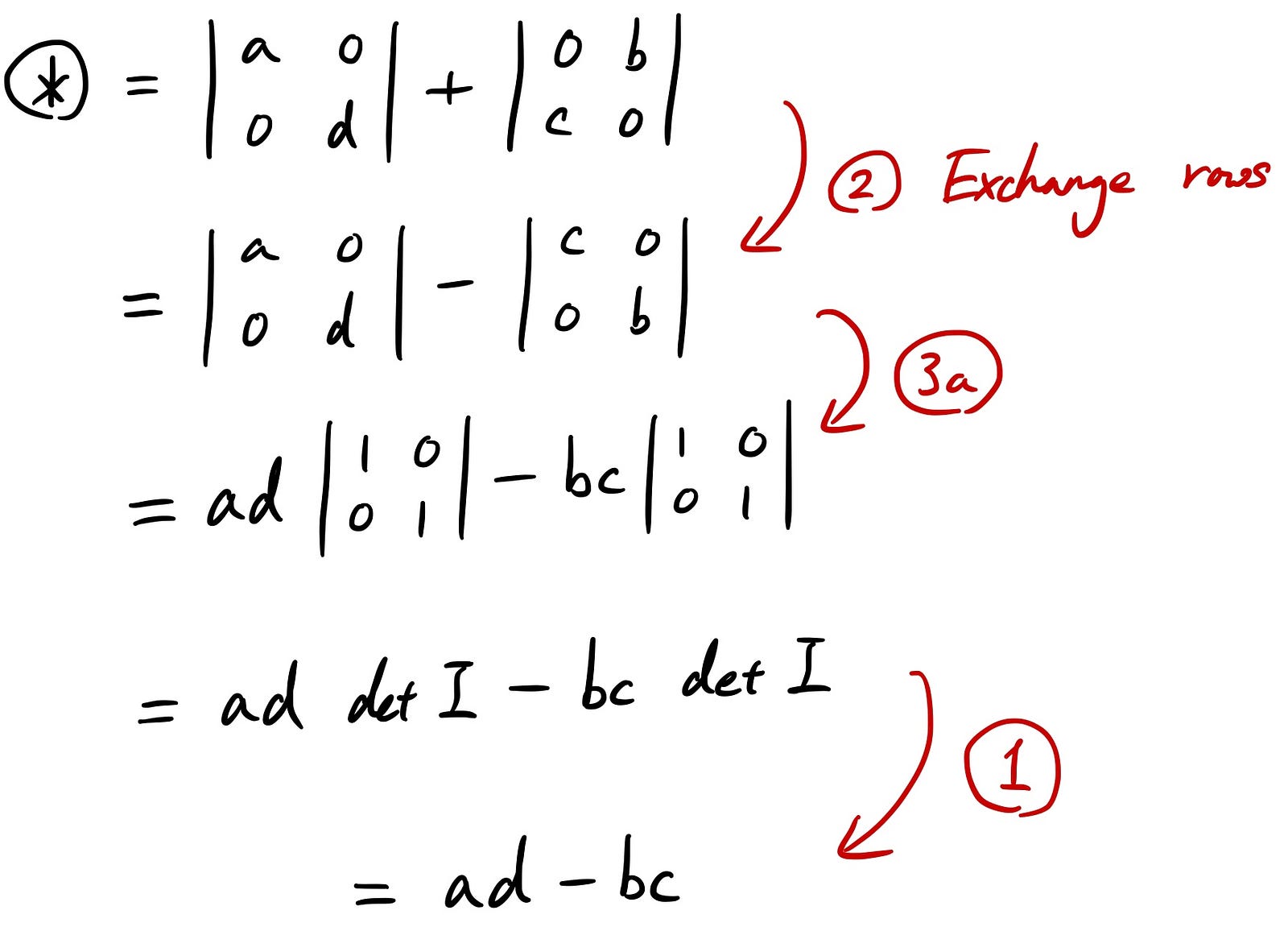
Great! Now I hope you know a lot about the properties and the determinant itself!