Lecture 3

課程內容記錄：（上）https://zhuanlan.zhihu.com/p/20918580?refer=intelligentunit

                         （中）https://zhuanlan.zhihu.com/p/20945670?refer=intelligentunit

                         （下）

1．線性分類器（linear classifer）：

我們總是希望得到一個函式f(x,w)，即評分函式（score function），x代表輸入資料，往往是影象的numpy矩陣，w是權重或者一些引數，而整個函式的結果對應預測值的一維Numpy矩陣，矩陣中數值最大的預測值代表概率最高的預測物件。我們可以去利用充分地想象力改變f，已得到儘可能高效準確的預測結果，最簡單的f就是乘積的形式，也就是線性分類器。

通常我們會新增一個偏置項，他是對應預測結果數的一維向量，它對預測得到的資料進行偏置，以獲得更具有取向性的結果（如果你的分類結果中貓的數量大於狗，而測試集中貓狗的數量一致，很可能你的偏置更傾向於貓）。

2．NN和線性分類器的區別：

NN的訓練過程只是將訓練集圖片及標籤提取出來，預測過程中找到與預測物件L1距離最小的訓練集影象，它對應的標籤類別就是預測類別。KNN多了一步是找到K個最小影象進行二次投票。

線性分類器需要得到權重值W和偏置值b，然後相當於利用測試影象去匹配不同類別對應的（W,b）組成的模板影象，最為匹配的則屬於該類別。這樣極大地節省了測試集測試所需的時間。這時我們所要做的“匹配”過程，是使預測影象得到的評分結果儘可能與訓練集中影象的真實類別一致，即評分函式在正確的分類位置應當得到最高的評分。（也就是說通過W，b劃分出分類的特定空間）

3．關於支援向量機（SVM：Support Vector Machine

支援向量機的基本模型是在特徵空間上找到最佳的分離超平面使得訓練集上正負樣本間隔最大，原用來解決二分類問題的有監督學習演算法，在引入了核方法之後SVM也可以用來解決非線性問題。離分離超平面最近的兩個資料點被稱為支援向量（Support Vector）。

參見吳恩達機器學習課程以及李航《統計學習方法》

4．關於正則化（regularization）:

通過在損失函式中加入後一項，正則化項，我們對W的值進行了制約，希望模型選擇更簡單的W值。這裡的“簡單”具體取決於你的模型種類和任務的規模。它同樣體現了奧卡姆剃刀的觀點：如果你找到了多個可以解釋結果的假設，一般來說我們應該選擇最簡約的假設。因為這樣的假設魯棒性更好，更適用於全新的測試集。基於這一思想，我們希望W的值儘量小。這樣我們的損失函式就具有兩個項，資料丟失項（data loss）和正則化項（Regularization）。這裡我們用到了一種超引數λ用以平衡這兩項，稱為正則化引數。

關於正則化引數部分，可以參見吳恩達課程。

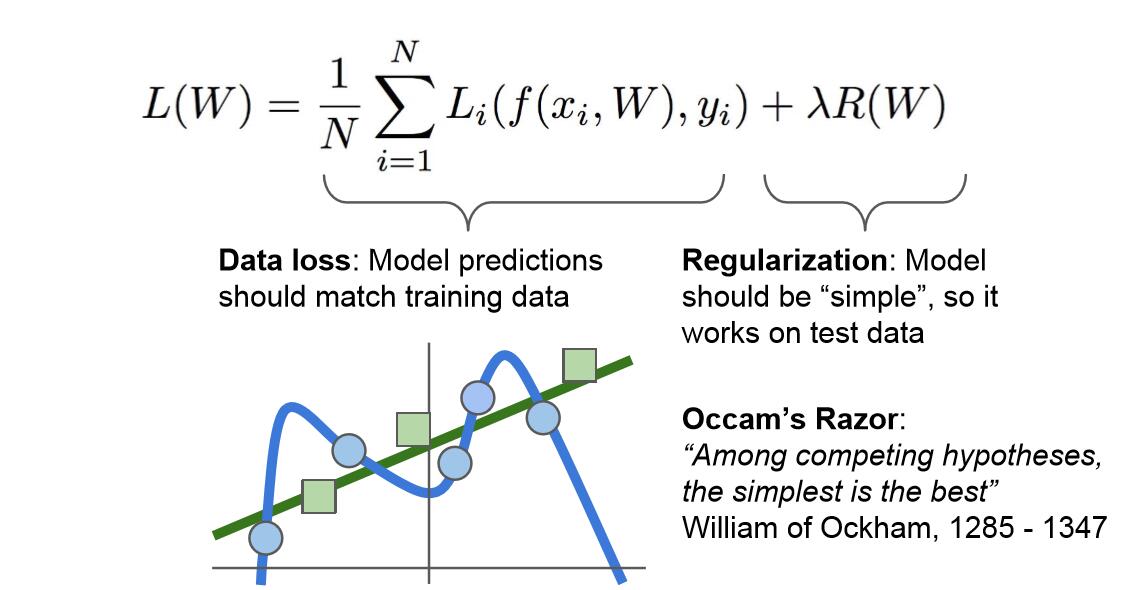
一些正則化方法如下圖：

對模型進行正則化（regulairzation），也就是在損失函式中加入正則項的主要目的是為了減輕模型的複雜度，在一定程度上減緩過擬合的速度。

5．關於範數（norm）:

參見：https://blog.csdn.net/a493823882/article/details/80569888

6．支援向量機（SVM）和Softmax分類器的對比:

SVM和Softmax是最常用的兩個分類器，Softmax的損失函式和SVM不同，SVM輸出f(x,W)，我們得到每個分類的對應的評分大小。而Softmax的輸出更加直觀，是各分類歸一化後的分類概率。在Softmax分類器中，函式f(x，W)=Wx的形式保持不變，但分類器將這些評分值視為每個分類的未歸一化的對數概率，並且將折葉損失（hinge loss）替換成了交叉熵損失（cross-entropy loss）。

關於交叉熵的解釋以及兩者區別的具體例子，以及關於兩者區別的一些解釋，課程筆記中講得很好。

注：

關於softmax對數取負的原因：我們將對數概率指數化，歸一化之後再取對數，這時如果結果越好當然概率越高，但我們期望loss應該越低才對，所以對結果取負。

Softmax Classifier，又稱Multinomial Logistic Regression，多項式邏輯迴歸。

7．loss function總結：