Lecture 6  Training Neural Networks

課堂筆記參見：https://zhuanlan.zhihu.com/p/22038289?refer=intelligentunit

本節課內容主要包括三部分：訓練前準備、訓練和評分。具體包括啟用函式的選擇，預處理，權重初始化，正則化，梯度檢查，監控學習程序，引數更新，超引數優化和最終的模型評估。

一、啟用函式

啟用函式就是f，在以往線性評分的基礎上加上啟用函式，引入了非線性項，整體作為評分。

1.     Sigmoid:

在絕對值較大的區域近似為線性函式，斜率很小。

這個函式在一定程度上可以看做是神經元的飽和放電率（firing rate）。

問題：

1.飽和神經元將導致梯度消失：當x絕對值比較大時,σ對x的偏導為0。x=0時，將得到一個合理的梯度，x=10，時，梯度將為0。

2.sigmoid並不是一個以0為中心值的函式，也就是說 Sigmoid 的輸出不是0均值的，這是我們不希望的，因為這會導致後層的神經元的輸入是非0均值的訊號，這會對梯度產生影響：假設後層神經元的輸入都為正, 對w求梯度時，L對w的偏導要麼全為正，要麼全為負，由dL/df決定（L是Loss，f是評分函式），而df/dw=x（w的區域性梯度）都為正，這樣在反向傳播的過程中w要麼都往正方向更新，要麼都往負方向更新，導致有一種捆綁的效果，使得收斂緩慢。

當然了，如果你是按batch去訓練，那麼每個batch可能得到不同的符號（正或負），那麼相加一下這個問題還是可以緩解。因此，非0均值這個問題雖然會產生一些不好的影響，不過跟上面提到的 kill gradients 問題相比還是要好很多的。

如下圖右側的例子，w為二維，f描述為f(x,w,b)=f(w0x0+w1x1+b)，現在假設w0，w1的最優解滿足藍色向量的條件，那麼梯度更新向藍色箭頭方向是最快的，這個更新方向要求dw0為正，dw1為負，也就要求輸入的x0，x1符號相反。但是，由於上個神經元sigmoid函式輸出的x0,x1始終符號相同，因此梯度更新只能走如圖所示的折線軌跡，收斂緩慢。

3.指數函式的計算代價比較高，但不是重點，因為卷積和點乘的計算代價更大。

2.     tanh:

和sigmoid主要的不同是以0為中心了，但是依然會存在梯度消失的問題。

3.     ReLU:

最大的優勢是不存在正值的梯度消失問題。計算成本也比較低，不含指數。通常我們使用ReLU比較多，因為它比sigmoid和tanh收斂快得多，大約快6倍。也有證據表明它比sigmoid更具備生物學上的合理性。

問題：不再以0為中心，負半軸依然會有梯度消失問題。當資料出現在負半軸的區域時，我們將之稱為dead ReLU。如果某節點設定的權值不合理，所有的輸入經過線性變換都小於0，那這個節點上的權重就沒法反向傳播更新，即為dead ReLU，此時dead ReLU的輸出也將都是0。當然如果learning rate比較大，權重更新幅度大，一開始正常的ReLU在之後也可能dead，當你使用一個訓練好的網路的時候，你會發現會有10%~20%的dead ReLU，大多數使用ReLU的網路都有這個問題。

所以一些人在使用ReLU的時候習慣用較小的正偏置來初始化ReLU（比如0.01），以期增加它在初始化時被啟用的可能性，但這在理論上並沒有被證明。

4.     Leaky ReLU:

Leaky ReLU是ReLU的一個改進，不會有任何的飽和問題，它仍然比sigmoid和tanh的收斂速度快，沒有dead problem。

另一個變形是引數整流器（parametric rectifier），簡稱PReLU，此時的α同樣參與反向傳播過程，因此更加靈活。

5.     Exponential Linear Units：（ELU）

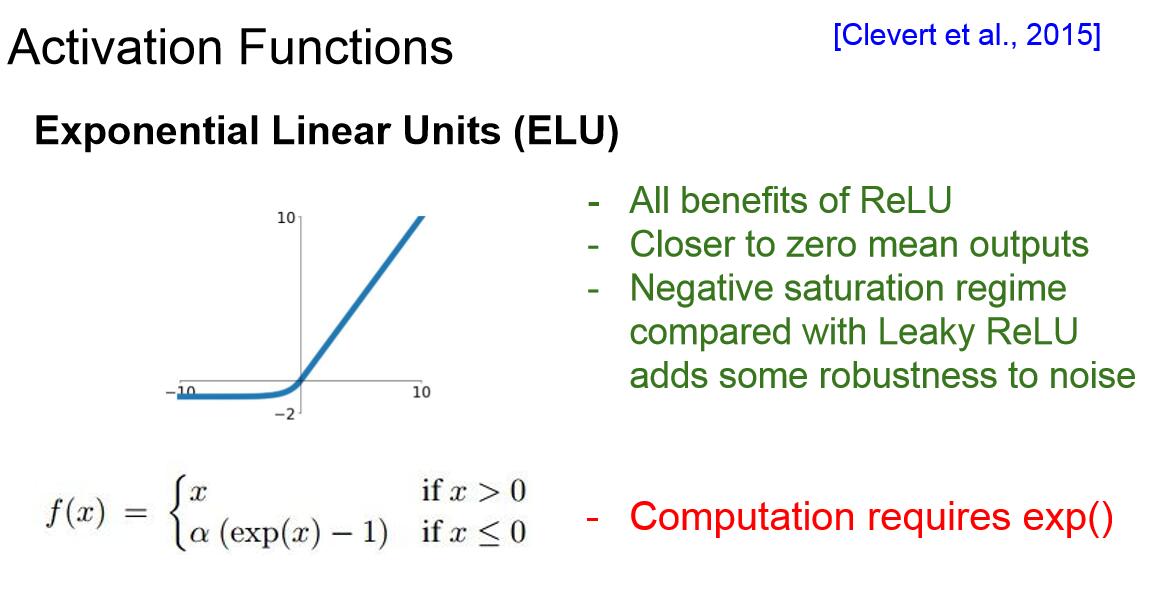
這種指數線性單元具有ReLU的一切優點，但是與Leaky ReLU相比，ELU並沒有在負區間傾斜，這裡實際上我們建立了一種負飽和機制，有一些觀點認為這樣做可以使模型對噪音有更強的魯棒性。這個模型可以被認為介於ReLU和Leaky ReLU之間。

6.     Maxout Neuron:

除了上面的各種ReLU變體之外，這裡還有一種最大輸出神經元的啟用結構，它翻倍了權重和偏置的數量，輸出其中較大的值，作用是泛化了ReLU和Leaky ReLU，因為與常規啟用函式不同的是,它是一個可學習的分段線性函式.

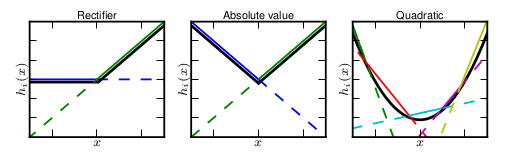
任何一個凸函式，都可以由線性分段函式進行逼近近似。ReLU、Leaky ReLU都可以看成是分段的線性函式，如下示意圖所示。那麼,前邊的兩種ReLU便是Maxout中兩個函式的組合，函式影象為兩組直線的拼接

7.     一般經驗:

一般做法是用ReLU，這是最標準的方法，你要謹慎地調整學習速率。你可以使用Leaky ReLU，Maxout，ELU，但是這些方法大多是實驗性的（實用性不強），你想要結合你的模型考慮。另外，我們一般不使用sigmoid，因為這是最原始的啟用函式，ReLU及變體表現得更好。

二、資料預處理

一些資料預處理的標準操作是拿到原始資料之後，零均值化（中心化），然後利用標準差進行歸一化。

關於零均值化，我們之前講過如果所有的輸入資料都是正的，那麼梯度也全是正的或者負的，這會導致我們的優化效果下降。在這節課中，我們經常會對影象資料零均值化，但是不總是進行歸一化操作，因為一般對於影象來說，畫素分佈總是較為均勻的。我們更不會去做像PCA或者白化這種更為複雜的預處理。在訓練資料中，我們會得到均值影象，這將會被運用到測試資料中。均值的獲取方法既可以是整張影象均值（AlexNet），也可以是各顏色通道的均值（VGGNet）。

三、權重初始化

如果我們使用0作為初始值，每層神經元在第一次資料輸入時就將得到相同的數值，並且得到相同的梯度，也會以相同的方式更新，這樣你得到的就是相同的神經元，這當然是不合適的，所以我們需要打破初始權重的一致性。所以我們希望權重是較小的隨機數，可以用高斯分佈取樣，比如下圖：

這種權重初始化適用於小型網路，但是對於更深的網路結構，對於一個10層的網路，每層有100個神經元，你就會發現除了第一層的啟用值滿足高斯分佈之外，後幾層的啟用值迅速下降為0，因為w的初始值太小了。如果我們計算梯度的話，w的梯度含有上一層的x輸入項，因此權重基本不會更新。

 當我們從高斯分佈中取樣，用1來乘以標準差而不是0.01時，權重過大將會導致網路飽和。所以權重過大或者過小都會導致結果不盡如人意。一個很好的經驗是我們可以使用如圖所示的Xavier初始化。（Xacier initialization. Glorot et al.，2010）。

這個公式的核心思想是讓輸出的方差和輸入的方差儘可能地保持一致。可以看到，輸出值在很多層之後依然保持著良好的分佈。需要注意的是，Xavier initialization是線上性函式的基礎上推導得出，這說明它對非線性函式並不具有普適性，所以這個例子僅僅說明它對tanh很有效，對於目前最常用的ReLU神經元，則不會適用，這時He initialization的表現更好。

參見：https://www.leiphone.com/news/201703/3qMp45aQtbxTdzmK.html

          https://zhuanlan.zhihu.com/p/21560667?refer=intelligentunit

四、Batch Normalization

Batch Normalization是一種巧妙而粗暴的方法來削弱bad initialization的影響，其基本思想是：If you want it, just make it!

我們想要的是在非線性activation之前，輸出值應該有比較好的分佈（例如高斯分佈），以便於back propagation時計算gradient，更新weight。Batch Normalization將輸出值強行做一次Gaussian Normalization和線性變換（如下圖）。

Batch Normalization中所有的操作都是平滑可導，這使得back propagation可以有效執行並學到相應的引數γ，β。需要注意的一點是Batch Normalization在training和testing時行為有所差別。Training時μβ和σβ由當前batch計算得出；在Testing時μβ和σβ應使用Training時儲存的均值或類似的經過處理的值，而不是由當前batch計算。

五、Babysitting the Learning Process（學習過程監測）

當我們初始化我們的網路的時候，我們想確定前向傳播的損失函式是合理的，這裡我們使用一個softmax分類器，當我們的初始權重很小，滿足分散分佈的時候，softmax的損失應當是負對數似然NLL的結果（均勻分佈），如果有十個分類項，就應該是1/10的負對數。

一旦我們看到我們的初始損失還不錯時，接下來我們加入零正則化項，再次檢查loss，然後啟動正則化，賦值比如1e3，可以看到損失值上升了。

現在我們開始訓練，從小資料集開始，小資料集可以幫助你快速調整模型，發現問題。我們先不用正則化操作，觀察是否能把訓練損失降為0，理想情況下我們可以觀察到，在多個epoch之後，我們的最終損失降為0，訓練集的準確率上升為1。

當你結束了所有的完整性檢查工作，就可以開始真正的訓練了。這時我們使用所有訓練資料，並加上一個小的正則化項。然後調整超引數以達到網路最好的效能，比如確定一個好的learning rate（通常在1e-3到1e-5之間）。

六、Hyperparameter Optimization

    如何選擇最佳的超引數值呢？我們使用的策略是交叉驗證（cross-validation），交叉驗證的意思是在訓練集上進行訓練，在驗證集上驗證，觀察這些超引數的效果。這裡我們有兩件事要做，首先我們選擇相當分散的數值，然後用幾個epoch進行學習，在訓練之後你就大體可以知道哪些超引數是有效的，這時你會得到一個引數的合適範圍，然後我們將在這個範圍內搜尋更精確的值。