資料學習(2)·廣義線性模型
作者課堂筆記,有問題請聯絡[email protected]
目錄
- 指數族,廣義線性模型
1 指數族
如果一種分佈可以寫成如下形式,那麼這種分佈屬於指數族: p(y;η)=b(y)eηTT(y)−a(η)
- η:分佈的自然引數
- T(y):充分統計量
- a(η):log的分隔函式(a(η)作為歸一化常量,目的是讓∑yp(y;η)=1)
1.1 伯努利分佈
分佈形式: p(y;ϕ)=ϕy(1−ϕ)1−y
- η=log(1−ϕϕ)
- b(y)=1
- T(y)=y
- a(η)=log(1+eη)
1.2 高斯分佈
y∼χ(μ,1) p(y;θ)=2π1e−2(y−μ)2
- η=μ
- b(y)=2π1e2y2
- T(y)=y
- a(η)=21η2
y∼χ(μ,σ2) p(y;θ)=2πσ21e−2σ2(y−μ)2
- η=[σ2μ−2σ21]
- b(y)=2π1
- T(y)=[yy2]
- a(η)=2σ2μ+logσ
1.3 柏鬆分佈
p(y;λ)=y!λye−λ
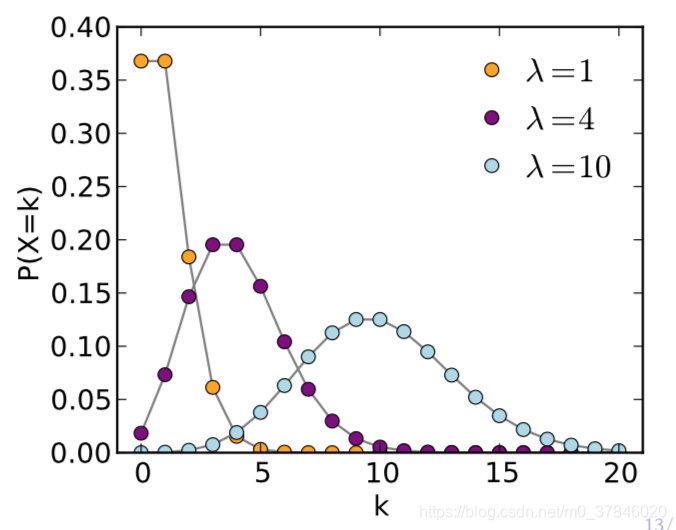
- η=log(λ)
- b(y)=y!1
- T(y)=y
- a(η)=eη
2 廣義線性模型
通過改變y的分佈,從而更好的擬合數據。是一種構造線性模型的方法,其中Y|X來自於指數族。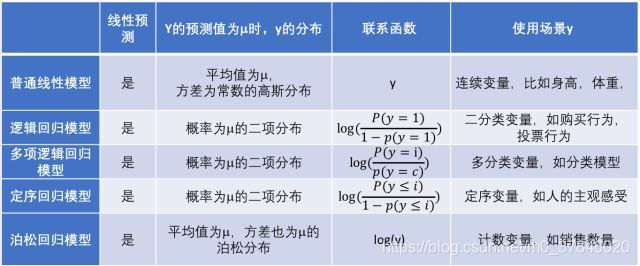
來源https://www.sohu.com/a/228212348_349736
廣義線性模型的設計初衷:
- 為了使響應變數y可以有任意的分佈。
- 允許任意的函式(連結函式)可以隨著輸入的x變化。
構建方法:
- y|x;θ∼指數族分佈(高斯、柏鬆、伯努利…)
- 我們的目標是給定x,預測T(y)的期望,大多數情況是T(y)=y,而在其他情況下可能是E[y|x;θ]
- 自然引數η和x是線性相關的,滿足η=θTx 如果問題滿足以上的三個假設,那麼我們那就可以構造廣義線性模型來解決問題。
2.1 最小二乘法
應用GLM的構造準則:
- y|x;θ∼N(μ,1) η=μ,T(y)=y
- 推導假設函式: hθ(x)=E[y∣x;θ]=μ=η
- 應用線性模型η=θTx hθ(x)=η=θTx 典範響應函式:μ=g(η)=η 典範連結函式:η=g−1(μ)=μ
2.2 Logistic迴歸
應用GLM的構造準則:
- y|x;θ∼Bernoulli(ϕ) η=log(1−ϕϕ),T(y)=y
- 推導假設函式: hθ(x)=E[y∣x;θ]=ϕ=1+e−η1
- 應用線性模型η=θTx
hθ(x)=1+e−θTx1
典範響應函式:ϕ=g(η)=sigmoid(η)
典範連結函式:η=g−1(ϕ)=logit(ϕ
相關推薦
資料學習(2)·廣義線性模型
作者課堂筆記,有問題請聯絡[email protected] 目錄 指數族,廣義線性模型 1 指數族 如果一種分佈可以寫成如下形式,那麼這種分佈屬於指數族: p(y;η)=b(y)e
python 機器學習 sklearn 廣義線性模型
廣義的線性模型是最最常用和我個人認為最重要的 最小二乘 class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=
機器學習數學原理(2)——廣義線性模型
機器學習數學原理(2)——廣義線性模型 這篇博文主要介紹的是在機器學習中的迴歸問題以及分類問題中的一個非常具有概括性的模型:廣義線性模型(Generalized Linear Models,簡稱GLMs),這類模型包括了迴歸問題中的正態分佈,也包含了分類問題中的伯努利分佈。隨著我們的
廣義線性模型2
nor alt 能夠 ever ... mat rcv shape dwt 1.1.2 Ridge Regression(嶺回歸) 嶺回歸和普通最小二乘法回歸的一個重要差別是前者對系數模的平方進行了限制。例如以下所看到的: In [1]: from sklearn im
廣義線性模型 - Andrew Ng機器學習公開課筆記1.6
sans luci art 能夠 tro ron 便是 import grand 在分類問題中我們如果: 他們都是廣義線性模型中的一個樣例,在理解廣義線性模型之前須要先理解指數分布族。 指數分
分類和邏輯回歸(Classification and logistic regression),廣義線性模型(Generalized Linear Models) ,生成學習算法(Generative Learning algorithms)
line learning nbsp ear 回歸 logs http zdb del 分類和邏輯回歸(Classification and logistic regression) http://www.cnblogs.com/czdbest/p/5768467.html
R語言學習筆記(十一):廣義線性模型
學習筆記 Education 5.0 1.3 style only 可能性 div erro #Logistic 回歸 install.packages("AER") data(Affairs,package="AER") summary(Affairs) a
線性迴歸_邏輯迴歸_廣義線性模型_斯坦福CS229_學習筆記
前言 之前學習過視訊版本的吳恩達老師CS229的機器學習課程,但是覺得並不能理解很好。現在結合講義,對於之前的內容再次進行梳理,仍然記錄下自己的思考。圖片來源於網路或者講義。話不多說,進入正題吧。 Part I Regression and Linear Regression
深度學習基礎--loss與啟用函式--廣義線性模型與各種各樣的啟用函式(配圖)
廣義線性模型是怎被應用在深度學習中? 深度學習從統計學角度,可以看做遞迴的廣義線性模型。廣義線性模型相對於經典的線性模型(y=wx+b),核心在於引入了連線函式g(.),形式變為:y=g(wx+b)。 深度學習時遞迴的廣義線性模型,神經元的啟用函式,即為廣義線性模型的連結函式
機器學習cs229——(三)區域性加權迴歸、邏輯迴歸、感知器、牛頓方法、廣義線性模型
首先,我們先來討論一下欠擬合(underfitting)和過擬合(overfitting)問題。比如我們同樣採用線性迴歸來對一組房屋價格和房屋大小的資料進行擬合,第一種情況下我們只選取一個數據特徵(比如房屋大小 x)採用直線進行擬合。第二種情況下選取兩個資料特徵(比如房屋大
第3章-從線性概率模型到廣義線性模型(2)
原文參考 斯坦福機器學習cs229-2-Generative Learning algorithms https://mathdept.iut.ac.ir/sites/mathdept.iut.ac.ir/files/AGRESTI.PDF http://data.princeton.edu
機器學習筆記五:廣義線性模型(GLM)
一.指數分佈族 在前面的筆記四里面,線性迴歸的模型中,我們有,而在logistic迴歸的模型裡面,有。事實上,這兩個分佈都是指數分佈族中的兩個特殊的模型。所以,接下來會仔細討論一下指數分佈族的一些特點,會證明上面兩個分佈為什麼是指數分佈族的特性情況以及怎麼用到
從線性模型到廣義線性模型(2)——引數估計、假設檢驗
本文系轉載,原文連結:http://cos.name/2011/01/how-does-glm-generalize-lm-fit-and-test/ 1.GLM引數估計——極大似然法 為了理論上簡化,這裡把GLM的分佈限定在指數分佈族。事實上,實際應用中
【機器學習-斯坦福】學習筆記4 ——牛頓方法;指數分佈族; 廣義線性模型(GLM)
牛頓方法 本次課程大綱: 1、 牛頓方法:對Logistic模型進行擬合 2、 指數分佈族 3、 廣義線性模型(GLM):聯絡Logistic迴歸和最小二乘模型 複習: Logistic迴歸:分類演算法 假設給定x以為引數的y=1和y=0的概率:
機器學習演算法之:指數族分佈與廣義線性模型
> 翻譯總結By joey周琦 參考NG的lecture note1 part3 本文將首先簡單介紹指數族分佈,然後介紹一下廣義線性模型(generalized linear model, GLM), 最後解釋了為什麼邏輯迴歸(logistic r
資料探勘,篩選,補充的廣義線性模型的---- LASSO 迴歸
Kaggle 網站(https://www.kaggle.com/)成立於 2010 年,是當下最流行的進行資料發掘和預測模型競賽的線上平臺。 與 Kaggle 合作的公司可以在網站上提出一個問題或者目標,同時提供相關資料,來自世界各地的電腦科學家、統計學家和建模愛好者, 將
斯坦福大學公開課機器學習課程(Andrew Ng)四牛頓方法與廣義線性模型
本次課所講主要內容: 1、 牛頓方法:對Logistic模型進行擬合 2、 指數分佈族 3、 廣義線性模型(GLM):聯絡Logistic迴歸和最小二乘模型 一、牛頓方法 牛頓方法與梯度下降法的功能一樣,都是對解空間進行搜尋的方法。 假設有函
廣義線性模型的理解
選擇 現象 one 世界 logistic 是什麽 times 自己 取值 世界中(大部分的)各種現象背後,都存在著可以解釋這些現象的規律。機器學習要做的,就是通過訓練模型,發現數據背後隱藏的規律,從而對新的數據做出合理的判斷。 雖然機器學習能夠自動地幫我們完成很多事情(
R語言-廣義線性模型
類別 模型 判斷 table height 函數 on() 手動 res 使用場景:結果變量是類別型,二值變量和多分類變量,不滿足正態分布 結果變量是計數型,並且他們的均值和方差都是相關的 解決方法:使用廣義線性模型,它包含費正太因變量的分析 1.Logisti
