ml課程:FM因子分解機介紹及相關程式碼
阿新 • • 發佈:2018-12-20
以下是我的學習筆記,以及總結,如有錯誤之處請不吝賜教。
FM(factorization machines)表示因子分解機,是由Steffen Rendle提出的一種基於矩陣分解的機器學習演算法。目前,被廣泛的應用於廣告預估模型中,相比LR而言,效果更好。主要目標是:解決資料稀疏的情況下,特徵怎樣組合的問題,因此該演算法主要用於組合特徵等特徵工程。
原理推倒:(參考1、參考2)
- 模型方程:基本線性迴歸模型的基礎上引入交叉項:

其中:xi,xj表示各特徵分量,(ij不相等),但是上式有個問題:對於觀察樣本中未出現過互動的特徵分量,不能對相應的引數進行估計。為克服該缺點,引入輔助變數:
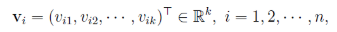 其中k為超引數,將wij改寫為:
其中k為超引數,將wij改寫為:
令vi=(vi1,vi2,...,vik)vi=(vi1,vi2,...,vik)。然後,利用vivTjvivjT對交叉項的係數ωijωij進行估計: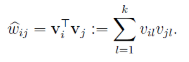
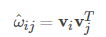
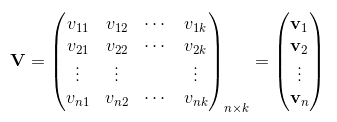
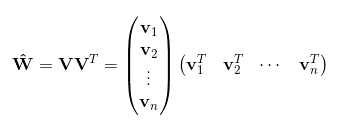
於是得到最終模型為:
- 計算複雜度:模型需要估計的引數包括:
共有1+n+nk個,那麼計算複雜度為: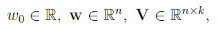
利用:((a+b+c)2−a2−b2−c2)/2((a+b+c)2−a2−b2−c2)/2求出交叉項,對上式第二項進行簡化: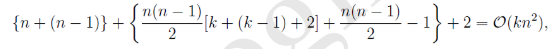
因此其時間複雜度降至O(kn):
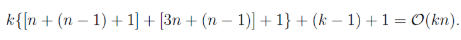
- 損失函式:
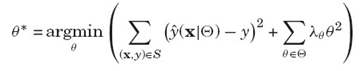
- 優化函式:主要有隨機梯度下降(SGD)、交替最小二乘(ALS)、馬爾科夫鏈蒙特卡羅法(MCMC),下面主要講交替最小二乘法(也稱座標下降法),基本思路是每次只對一個引數進行優化,並逐輪迭代:
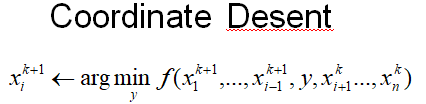
通過求其解析解得到:
引入殘差進行計算: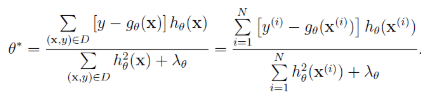
得到最終結果:
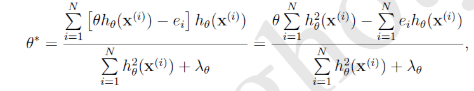
- 特點:與SGD相比,每次引數更新依賴上一輪所有的引數計算模型的殘差:
 沒有學習速率引數,每次更新時,記憶體需要load所有引數。
沒有學習速率引數,每次更新時,記憶體需要load所有引數。 - 優化方法比較:

- 與多項式迴歸的對比:
區別在於:當觀測資料非常稀疏的情況下,FM依然能夠估計出pairwise interactions,因為pairwise的權重是k維因子向量的乘積,而多項式迴歸的pairwise的權重假設是相互獨立的。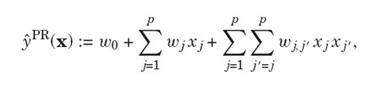
案例程式碼:
from pyfm import pylibfm from sklearn.feature_extraction import DictVectorizer import numpy as np train = [ {"user": "1", "item": "5", "age": 19}, {"user": "2", "item": "43", "age": 33}, {"user": "3", "item": "20", "age": 55}, {"user": "4", "item": "10", "age": 20}, ] v = DictVectorizer() X = v.fit_transform(train) print(X.toarray()) y = np.repeat(1.0,X.shape[0]) fm = pylibfm.FM( num_iter=10) fm.fit(X,y)
輸出:

fm.predict(v.transform({"user": "1", "item": "10", "age": 24}))輸出:![]()
To be continue......
