什麼是黎曼和？什麼是定積分？
在初等數學中學習了三角形，四邊形，多邊形的面積計算：
現在來學習 的面積是如何定義的，以及如何計算的：
1 拋物線下的曲邊梯形
1.1 問題
之前介紹過，要求 ，
之間的曲邊梯形的面積
：
可以把 均分為
份，以每一份線段為底，以這一份線段的右側的函式值為高做矩形：
當 的時候，矩形面積和就是曲面下的面積：
那麼，能不能以這一份的線段的左側的函式值為高做矩形？
1.2 計算
算一算就知道了。先把 均分成
份，每份長為
，以及各個劃分點的座標如下：
把座標組成兩個集合：
因此，以左側的函式值為高的矩形和可以如下計算：
同樣的道理，可以得到以右側的函式值為高的矩形和：
當 的時候，兩者是相等的，它們都是曲邊梯形的面積：
2 狄利克雷函式的曲邊梯形
之前介紹連續的時候就介紹過狄利克雷函式：
也見識過它的古怪性質。這裡也要把它拉出來作一個反面典型。 的影象是沒有辦法畫的，非要畫也就是這樣的：
假設要求 內的曲邊梯形面積，嘗試對
進行
等分，那麼等分點必然為有理數點（下圖為了演示方便，調整了下
座標的比例）：
所以這些等分點的函式值必然為1。以1為高，以等分割槽間長度為底作矩形，可以得到：
這些矩形的和必然為1，可以想象進行 等分也依然為1，所以有：
下面換一種劃分方式，以鄰近的兩個無理數作為端點劃分區間，這些區間的端點的函式值必然為0，以區間長度為底，0為高，得到的矩形和為：
可見，對於 而言，不同的劃分區間、不同的高的取法，會導致不同的矩形和：
3 黎曼和
格奧爾格·弗雷德里希·波恩哈德·黎曼（1826－1866）是德國數學家，黎曼幾何學創始人，複變函式論創始人之一。在數學界搞風搞雨的黎曼猜想也是他的傑作。
基於對剛才兩種情況：
-
拋物線下的曲邊梯形
-
狄利克雷函式下的曲邊梯形
的思考，看到不同劃分帶來的效果，黎曼先發明瞭黎曼和，進而定義了曲邊梯形的面積，也就是定積分。
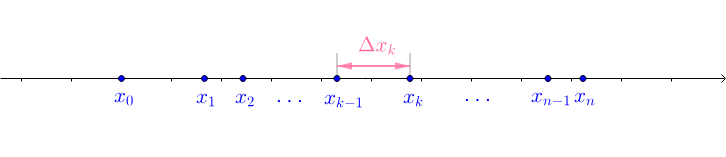
3.1 任意劃分
不一定需要均分為
份，可以任意分割：
很顯然用於分割區間的點符合：
令 ，那麼集合：
稱為 的一個
。劃分
定義了
個子區間：
稱為第
個子區間，更一般的
被稱為第
個子區間：
第 個子區間的長度為
：
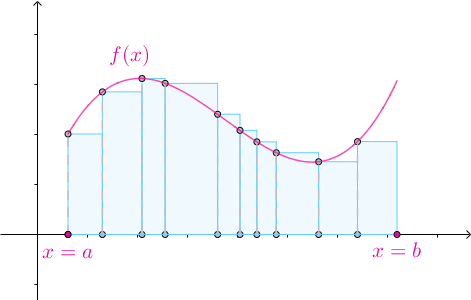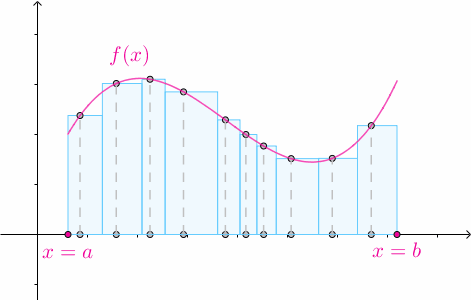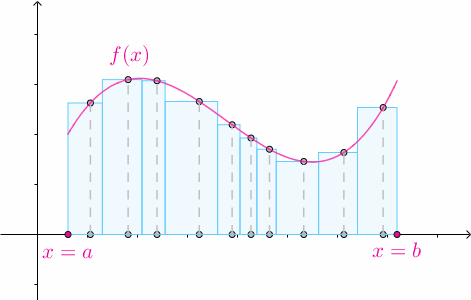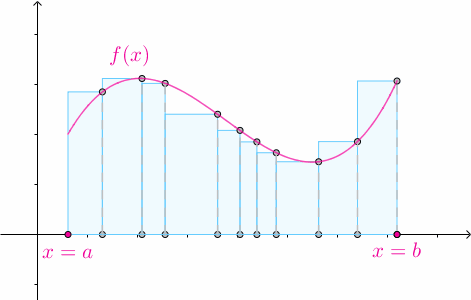
3.2 任意高度
對於某一個劃分 ，在其第
個子區間內隨便選一個數
：
以 作為矩形的高：
那麼矩形的高度也可以是任意的：
3.3 黎曼和
根據剛才的講解，可以得到如下定義：
設函式在
上有定義，在
這些分點的集合：
稱為
。劃分
定義了
個子區間：
它們的長度依次為：
在每個子區間
上任取選取一個數
，以
為高構造矩形，這些矩形的和：
稱為
在
。
之前計算的 、
是黎曼和：
狄利克雷函式中劃分出來的矩形和 、
也是黎曼和。
4 定積分
隨著 的劃分不斷變細，所有子區間的長度趨於0時，黎曼和不斷地逼近曲邊梯形的面積：
這個過程的嚴格化如下：
設函式，記：
如果下述極限存在：
則稱
在
上
，
為
，
為
，
為
，
為
，可以標記如下：
回到之前討論的問題：
-
拋物線下的曲邊梯形：
，以及各種劃分都相等，所以
-
狄利克雷函式下的曲邊梯形：
，所以
這裡新引入的積分符號是萊布尼茲創造的：
其中， 代表英文中的求和（“sum”），拉長的
則表明積分是和的極限（“limits of sums”）。這個符號相當精練，可以表達非常豐富的資訊：
最新版本（可能有不定期更新）：黎曼和與定積分