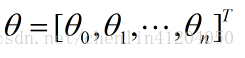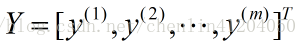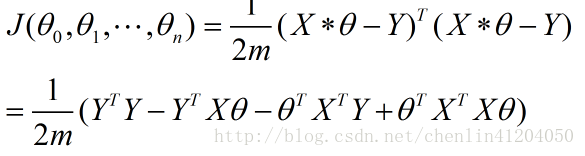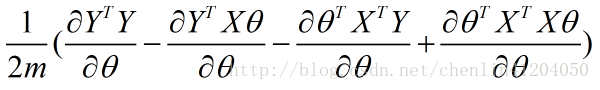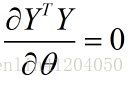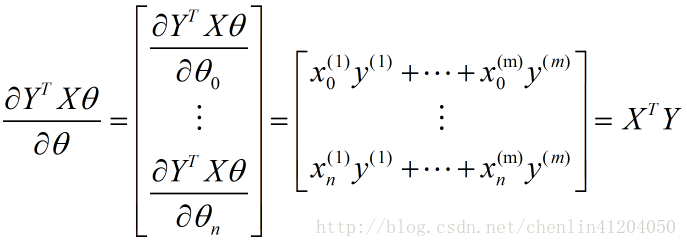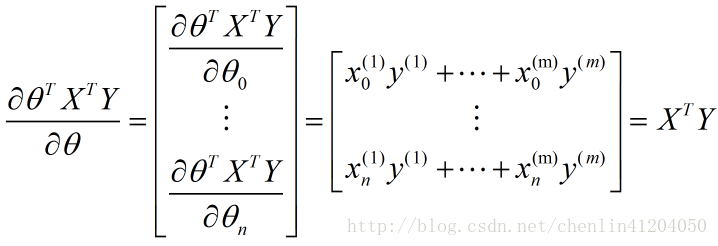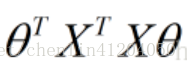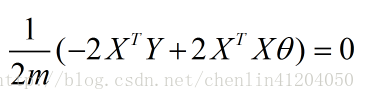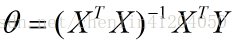正規方程求解特徵引數的推導過程
多變數線性迴歸代價函式為:
正規方程是通過求解下面的方程來找出使得代價函式最小的引數:
設有m個訓練例項,每個例項有n個特徵,則訓練例項集為:
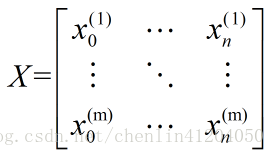
其中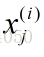
特徵引數為:
輸出變數為:
故代價函式為:
進行求導,等價於如下的形式:
- 其中第一項:
- 第二項:
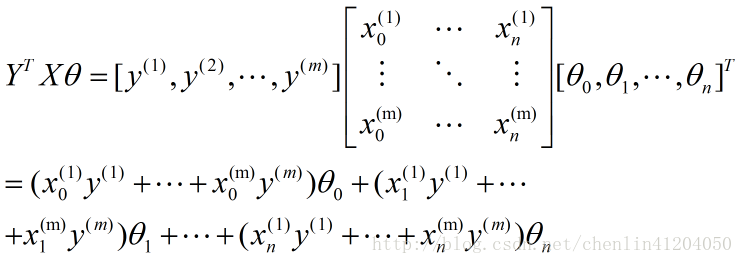
該矩陣求導為分母佈局下的標量/向量形式:
故有,
- 第三項:
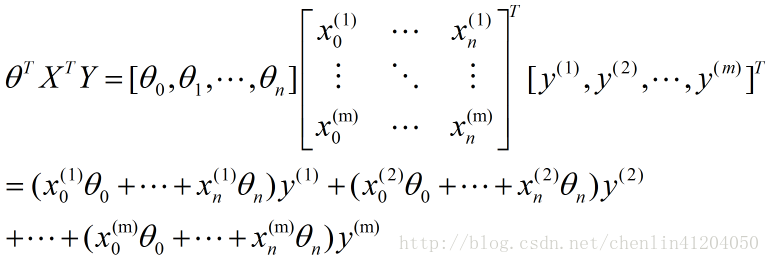
該矩陣求導為分母佈局下的標量/向量形式:
故有:
- 第四項:
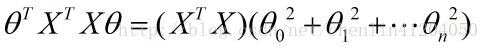
其中
該矩陣求導為分母佈局下的標量/向量形式:
故有:
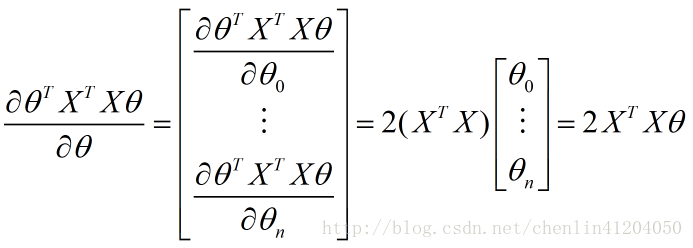
綜上,正規方程為:
最終可得特徵引數的表示:
相關推薦
正規方程求解特徵引數的推導過程
多變數線性迴歸代價函式為: 其中: 正規方程是通過求解下面的方程來找出使得代價函式最小的引數: 設有m個訓練例項,每個例項有n個特徵,則訓練例項集為: 其中表示第i個例項第j個特徵。 特徵引數為: 輸出變數為: 故代價函式為:
利用批量梯度下降和正規方程求解線性迴歸引數的理論推導
有一組房子的面積和價格資料,如下表所示: x(size)
利用批量梯度下降和正規方程求解線性迴歸引數(Python實現)
說明:本文使用的工具為Python3+Jupyter Notebook。 利用批量梯度下降 先匯入要用到的各種包: %matplotlib notebook import numpy as np import pandas as pd import matplotlib.pyplot a
機器學習:正規方程(Normal Equation)的推導
在coursera上看了Andrew Ng的《Machine Learning》課程,裡面講到了正規方程(Normal Equation),現在在此記錄一下推導過程。 假設函式(Hypothesis Function)為: hθ(x)=θ0+θ1x1+θ2x2
吳恩達機器學習(三)正規方程(求解線性迴歸引數)
目錄 0. 前言 學習完吳恩達老師機器學習課程的多變數線性迴歸,簡單的做個筆記。文中部分描述屬於個人消化後的理解,僅供參考。 0. 前言 線上性迴歸中,通常採用梯度下降,不斷迭代
正規方程推導(Normal equation)
微積分差不多都還回去了 法一: m 為
語音特徵引數MFCC提取過程詳解
原來對語音特徵引數MFCC的提取過程不是很瞭解,最近做實驗需要自己手動去提取,所以藉此機會,深入的學習了一下,所以記錄下來,希望能夠對日後的學習有一定的幫助。 一、MFCC概述 在語音識別(Spee
使用collapsed gibbs sampling對LDA中引數進行估計的推導過程
使用來表示文件--主題分佈的超引數,使用來表示主題--詞彙分佈的超引數,這些超引數的先驗分佈被定義在一個狄利克萊分佈中,如下所示: 在給定引數的情況下,所有隱變數(主題)的概率被定義在一個多項式分佈中,其中表示在文件m中,被賦給主題k的詞彙數量。 在給定引數的情況下,所有
SVM推導過程及SMO詳細求解過程(二)
記得當時自己在記筆記的時候,推導的過程中有一個地方符號寫錯了,有找到的嗎? 當時的推導花費了很多功夫,如果轉載請註明出處,謝謝! 其它:由於BLOG中公式編輯不方便,為了大家能夠容易閱讀,所以採用圖片
斯坦福大學機器學習筆記——特徵和多項式迴歸以及正規方程
我們可以舉一個例子來引入多項式迴歸: 比如我們之前遇到的房價問題,對於房價的影響我們假設有兩個特徵,一個是房子的寬度x1,另外一個是房子的長度x2,這針對房價的估測我們可以建立下面形式的假設: hθ
解釋一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推導過程(轉載)
線性不可分 itl 專註 out center forest 測試 重要 原因 KPCA,中文名稱”核主成分分析“,是對PCA算法的非線性擴展,言外之意,PCA是線性的,其對於非線性數據往往顯得無能為力,例如,不同人之間的人臉圖像,肯定存在非線性關系,自己做的基於ORL數據
機器學習-吳恩達-正規方程多變量回歸公式
com .cn bsp 學習 http ria family mage -1 矩陣的跡 A為nXn的矩陣 機器學習-吳恩達-正規方程多變量回歸公式
正規方程
width 叠代算法 我們 找到 mage 如果 梯度 ima 計算 梯度下降提供了一種最小化J的方法。讓我們討論第二種方法,這一次顯式地執行最小化,而不用叠代算法。在“方程”的方法,我們將最大限度地減少J通過明確其衍生物相對於θJ的,並使其為零。這使我們能夠在沒有叠代的情
SVM推導過程
SVM 機器學習 SVM推導過程
洛谷 [P1024]一元三次方程求解【二分答案】
https 格式 -m 要求 ble 方程 print else 如果 題目鏈接:https://www.luogu.org/problemnew/show/P1024 題目描述 有形如:ax3+bx2+cx+d=0 這樣的一個一元三次方程。給出該方程中各項的系數(a,
luogu1024 一元三次方程求解
iostream ble tar names 註意 stream 左右 ret == 題目大意 已知一元三次方程\(ax^3+bx^2+cx+d=0\): 有且只有3個根 對\(\forall x, x\in[-100,100]\) 對\(\forall x_1,x_2,
洛谷 P1024 一元三次方程求解
cstring stream () pro fin targe target bsp reg 洛谷 P1024 一元三次方程求解 題目描述 有形如: ax3 + bx2 + cx1 + dx0 = 0 這樣的一個一元三次方程。給出該方程中各項的系數( a,b,c
機器學習之——正規方程法
計算 很多 矩陣 運行 比較 梯度下降 nbsp 梯度 缺點 1.梯度下降法 (1)需要選擇學習率a (2)需要多次叠代 優點:梯度下降法在特征變量很多的情況下也能運行地相當好 2.正規方程法 (1)不需要選擇學習率a (2)不需要叠代 (3) 正規方程法不需要做特征縮放
機器學習:線性回歸——理論與代碼實現(基於正規方程與梯度下降)
overfit 返回 pen ear 隨機梯度 是否 很大的 建模 回歸 一 線性模型 給定由n個屬性描述的列向量\(f(\mathbf{x})={(x^{(1)};x^{(2)};...;x^{(n)})}\),其中 \(x^{(j)}\)是\(\textbf{x}\)
神經網絡的BP推導過程
size 附錄 strong 如何 技術分享 由於 pan 設置 預測 神經網絡的BP推導過程 下面我們從一個簡單的例子入手考慮如何從數學上計算代價函數的梯度,考慮如下簡單的神經網絡,該神經網絡有三層神經元,對應的兩個權重矩陣,為了計算梯度我們只需要計算兩個偏導數即可: