遞迴

（百度百科）

遞迴演算法（英語：recursion algorithm）

在電腦科學中是指一種通過重複將問題分解為同類的子問題而解決問題的方法。遞迴式方法可以被用於解決很多的電腦科學問題，因此它是電腦科學中十分重要的一個概念。絕大多數程式語言支援函式的自呼叫，在這些語言中函式可以通過呼叫自身來進行遞迴。計算理論可以證明遞迴的作用可以完全取代迴圈，因此在很多函式程式語言（如Scheme）中習慣用遞迴來實現迴圈。

1. 一個人趕著鴨子去每個村莊賣，每經過一個村子賣去所趕鴨子的一半又一隻。這樣他經過了七個村子後還剩兩隻鴨子，問他出發時共趕多少隻鴨子？經過每個村子賣出多少隻鴨子？

1. 分析：

設經過的村子為n (n = 0,1,2,...,7)，根據題目分析可知遞迴結束的出口: n = 7時，剩餘鴨子數rest = 2;

分析遞迴體：從後向前推 n=7時 ，reset = 2， 由於每經過一個村子，賣去所趕鴨子的一半又一隻，因此七個村子後剩餘的鴨子數 rest[7] = rest[6] - (rest[6]/2 + 1)

反推rest[6] = (rest[7] + 1) * 2

最終遞迴體: (rest[n+1] + 1) * 2;

綜上   n=7      rest=2

 0<=n<7     rest=(rest(n+1) + 1) * 2

/*
	date：2018年11月15日10:15:19
	author：Zoey
	description：一個人趕鴨子去每個村莊賣，每經一個村子賣去所趕鴨子的一半又一隻，這樣他經過了七個村子後還剩兩隻鴨子
	             問：他出發前趕了多少隻鴨子，經過每個村莊賣了多少隻鴨子？
	analysis：設經過的村子為n (n = 0,1,2,...,7)，根據題目分析可知遞迴結束的出口: n = 7時，剩餘鴨子數rest = 2;
	          分析遞迴體：從後向前推
			              n=7時 ，reset = 2
			              由於每經過一個村子，賣去所趕鴨子的一半又一隻
			              因此七個村子後剩餘的鴨子數 rest[7] = rest[6] - (rest[6]/2 + 1) 
						  反推rest[6] = (rest[7] + 1) * 2
						  最終遞迴體: (rest[n+1] + 1) * 2;
			  綜上   n=7      rest=2
			       0<=n<7     rest=(rest(n+1) + 1) * 2
*/
#include<stdio.h>

//形參n表示經過的村莊數，返回經過n個村莊後剩餘的鴨子數
int leftDucksNum(int n)
{
	if(n == 7)   //根據題目描述：當經過第七個村莊後，返回剩餘鴨子數為2
		return 2;
	else
		return 2*(leftDucksNum(n+1)+1);    //遞迴體
}


//計算經過每個村子後賣出的鴨子數 
int sellDucks() {	
	//遍歷經過每一個村莊後餘下的鴨子數目和賣出去的鴨子
	for(int i=1; i<8; i++)
	{
		printf("第%d村莊賣出鴨子數為：%d,剩餘鴨子數為：%d\n", i, (leftDucksNum(i-1)/2+1), leftDucksNum(i));   //賣出數為前一個村莊剩餘數除2加1 
	}
	return 0;
} 


void main()
{
	printf("鴨子的總數：%d\n", leftDucksNum(0));     //當n=0時，表示鴨子的總數
	sellDucks();
}
 

（2）執行結果

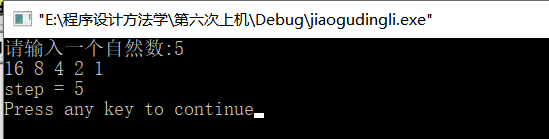
2.角谷定理。輸入一個自然數，若為偶數，則把它除以2，若為奇數，則把它乘以3加1。經過如此有限次運算後，總可以得到自然數值1。求經過多少次可得到自然數1。

如：輸入22，

輸出 2211 34 17 52 26 13 40 20 10 5 16 8 4 2 1

 STEP=16

1. 分析

遞迴出口：當輸入的數字為1時，則直接輸出

遞迴體：當輸入資料不為1時

當資料為偶數：除以2,遞迴直到資料為1，輸出

當資料為奇數：乘3再加1，遞迴直至資料為1，輸出

/*
  date:2018年11月15日
  author:Zoey
  description：角谷定理：輸入一個自然數，若為偶數，則把它除以2，若為奇數，則把它乘以3加1。經過如此有限次運算後，總可以得到自然數值1。求經過多少次可得到自然數1。
               如：輸入22，
               輸出 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
               STEP=16
*/

#include<stdio.h>

//角谷定理的實現，返回運算次數
int jiaogu(int step, int num)
{
	//遞迴出口
	//當輸入資料num = 1時，直接輸出num和預設運算次數0
	if(1 == num)
	{
		return step;
	}
	//當輸入偶數時，num/2，step+1，遞迴直至num = 1，輸出每次除2所得資料和次數
	else if(0 == num % 2)
	{
		printf("%d ", num/2);     //輸出運算中間資料
		++step;       //次數加一
		return jiaogu(step,num/2);      //遞迴體定於，返回運算次數
	}
	//輸入資料為奇數時，num*3 + 1 step++  遞迴直至num = 1，輸出資料和次數
	else
	{
		printf("%d ", num*3 + 1);
		++step;  //次數加一
		return jiaogu(step, num*3 + 1);   //遞迴體，返回運算次數
	}
}

void main()
{
	int num;
	int step = 0;//step=0表示當輸入的數字num=1時，直接輸出1，不需要進行運算
	printf("請輸入一個自然數:");
	scanf("%d", &num);
	printf("\nstep = %d\n", jiaogu(step, num));
}
 

（2）執行結果

3.電話號碼對應的字元組合：在電話或者手機上，一個數字如2對應著字母ABC，7對應著PQRS。那麼數字串27所對應的字元的可能組合就有3*4=12種（如AP，BR等）。現在輸入一個3到11位長的電話號碼，請打印出這個電話號碼所對應的字元的所有可能組合和組合數。

（1）分析：

數字num = 0 1 2 3 4 5 6 7 8 9;

每個數字對應的字母：" ", " ", "ABC","DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ";

將每個數字對應的字串儲存在一個二維陣列strArray中,陣列的索引即為每個字串對應的數字號碼.

首先將問題簡單化，若電話號碼只有一位數，比如說4，那麼其代表的單詞為g,h,i,

接著若電話號碼升級到兩位數，比如42： 分兩步走，從左到右，在選擇一個第一位數字所代表的字元的基礎上，遍歷第二位數字所代表的字元，直到遍歷完第一位數字代表的所有字元。

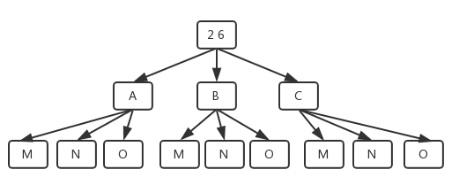
4所能代表的字元為ghi,2所能代表的字元為abc,首先讓4代表g，接著遍歷2所能代表的所有字元，即可得到ga,gb,gc,

然後再讓4代表h，再次遍歷2所能代表的所有字元，

即可得到ha,hb,hc,最後讓4代表i，那麼同理可得到ia,ib,ic。

遞迴求解

    遞迴出口：當輸入一個數字時，返回這個數字所有可能的字元組合

    遞迴體：當輸入多個數字時，每一個數字代表不同的字母（字串），返回最後一個數字及前面產生的每一個數字對應字元進行組合

/*
date:2018年11月16日14:15:09
author：Zoey
description： 電話號碼對應的字元組合：在電話或者手機上，一個數字如2對應著字母ABC，7對應著PQRS。
              那麼數字串27所對應的字元的可能組合就有3*4=12種（如AP，BR等）。
              現在輸入一個3到11位長的電話號碼，請打印出這個電話號碼所對應的字元的所有可能組合和組合數。
analysis: 數字num = 0 1 2 3 4 5 6 7 8 9;
          每個數字對應的字母：" ", " ", "ABC","DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ";
		  將每個數字對應的字串儲存在一個二維陣列strArray中,陣列的索引即為每個字串對應的數字號碼.
		  首先將問題簡單化，若電話號碼只有一位數，比如說4，那麼其代表的單詞為g,h,i,
          接著若電話號碼升級到兩位數，比如42
		  分兩步走，從左到右，在選擇一個第一位數字所代表的字元的基礎上，遍歷第二位數字所代表的字元，直到遍歷完第一位數字代表的所有字元。
		  就拿42來說，4所能代表的字元為ghi,2所能代表的字元為abc,首先讓4代表g，接著遍歷2所能代表的所有字元，即可得到ga,gb,gc,
		  然後再讓4代表h，再次遍歷2所能代表的所有字元，
		  即可得到ha,hb,hc,最後讓4代表i，那麼同理可得到ia,ib,ic。

		  遞迴求解
          遞迴出口：當輸入一個數字時，返回這個數字所有可能的字元組合
          遞迴體：當輸入多個數字時，每一個數字代表不同的字母（字串），返回最後一個數字及前面產生的每一個數字對應字元進行組合

          求解：利用函式遍歷和組合字母
*/
#include<stdio.h>
/*將每個數字所能代表的字母記錄在一個二維陣列c中，其中0、1代表沒有對應的字串*/
/*
	" ",      0
	" ",      1
	"ABC",    2
	"DEF",    3
	"GHI",    4
	"JKL",    5
	"MNO",    6
	"PQRS",   7
	"TUV",    8
	"WXYZ"    9
*/
char strArray[10][10] = {" ", " ", "ABC","DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ"};
//將每個數字所能代表的字母的總數記錄在total陣列中
int sum[10] = {0, 0, 3, 3, 3, 3, 3, 4, 3, 4};

/*index是指對電話號碼的第幾位進行操作，n是電話號碼的位數*/
/*遞迴初始呼叫為calculate(number, answer, 0, n)*/
void calculate(int * teleNumber, int * answer, int index, int n)
{

	//判斷是否為最後一位
    if(index == n)
    {
        for(int i = 0; i < n; i++)
		{
            printf("%c ", strArray[teleNumber[i]][answer[i]]);
		
		}
		printf("\n");
		return;   //遞迴出口

    }
	//遞迴體
	for(int i=0; i<sum[teleNumber[index]]; i++){
        answer[index] = i;
        calculate(teleNumber,answer,index+1,n);
    }
	//如果數字無對應字串，則輸出0，接著遞迴下一個數字
    if(sum[teleNumber[index]] == 0){
        answer[index] = 0;
        calculate(teleNumber,answer,index+1,n);
    }
}


void main()
{
	int teleLen;  //電話號碼位數
	//將電話號碼記錄在number陣列中
	int teleNumber[11];			
	/*
	將數字目前所代表的字母在strArray陣列中的列數下標記錄在answer陣列中
	初始化時answer[i] = 0
	*/
	int answer[11] = {0};
	printf("請輸入電話號碼的長度：");
	scanf("%d", &teleLen);     //輸入電話號碼位數

	printf("請輸入一個電話號碼：");
	for(int i=0; i<teleLen; i++)
		scanf("%d", teleNumber+i);

	calculate(teleNumber, answer, 0, teleLen);
}

(2)執行結果

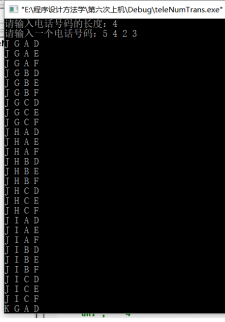
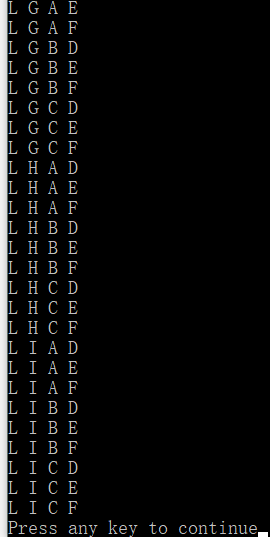
4.日本著名數學遊戲專家中村義作教授提出這樣一個問題：父親將2520個桔子分給六個兒子。分完 後父親說：“老大將分給你的桔子的1/8給老二；老二拿到後連同原先的桔子分1/7給老三；老三拿到後連同原先的桔子分1/6給老四；老四拿到後連同原先的桔子分1/5給老五；老五拿到後連同原先的桔子分1/4給老六；老六拿到後連同原先的桔子分1/3給老大”。結果大家手中的桔子正好一樣多。問六兄弟原來手中各有多少桔子？

（1）分析：

遞迴出口：老大得到老六分給的桔子後，每個人的桔子總數為總數的平均即2520/6=420個

          針對老大所得桔子數 = (420 - 從老六那裡所得桔子數)*7/8, 老六分給老大其1/3之後剩餘420個，因此他有420*3/2 = 630個桔子，即分給老大210個

  則可以算出老大在得到老六桔子之前有420-210 = 210個由於老大將其1/8分給老二，則可算出老大最初擁有240個桔子

/*
date:2018年11月16日22:17:16
author: Zoey
description：父親將2520個桔子分給六個兒子。分完 後父親說：“
			老大將分給你的桔子的1/8給老二；
			老二拿到後連同原先的桔子分1/7給老三；
			老三拿到後連同原先的桔子分1/6給老四；
			老四拿到後連同原先的桔子分1/5給老五；
			老五拿到後連同原先的桔子分1/4給老六；
			老六拿到後連同原先的桔子分1/3給老大”。
			結果大家手中的桔子正好一樣多。問六兄弟原來手中各有多少桔子？
analysis：遞迴出口：老大得到老六分給的桔子後，每個人的桔子總數為總數的平均即2520/6=420個
          針對老大所得桔子數 = (420 - 從老六那裡所得桔子數)*7/8, 老六分給老大其1/3之後剩餘420個，因此他有420*3/2 = 630個桔子，即分給老大210個
		  則可以算出老大在得到老六桔子之前有420-210 = 210個由於老大將其1/8分給老二，則可算出老大最初擁有240個桔子
		  然後每個兒子推算過程同老大
*/
#include<stdio.h>

//分桔子的實現，orangNum表示最開始擁有的桔子數，givenNum表示得到的桔子數，其中n表示分母的大小
void splitOranges(int sonNum, int orangeNum, int givenNum, int n)    
{
	if(sonNum > 6)  //如果兒子編號超過6，退出   遞迴出口
	{
		return;
	}
	int son[6] = {1,2,3,4,5,6};  //兒子的個數
	printf("第 %d 個兒子最初有 %d 個桔子\n", son[sonNum-1], orangeNum);
	int nextSon = 420 * (n-1)/(n-2) - givenNum/n;   //下一個兒子最初擁有的桔子數
	int nextSumNum = nextSon + givenNum/n;  //計算下一個兒子得到分配桔子數後的總桔子數
	splitOranges(sonNum+1, nextSon, nextSumNum, n-1);  //遞迴體
}
void main()
{
	splitOranges(1,240, 210, 8);  //引數表示為老大的桔子總數，老大被分配的桔子數和老大分給老二比例的分母
}

（2）執行結果