問題背景：本次我們來求取 f(x) = -2x^3 + 5x^2 + 9，這個函式，在給定區間[1.0, 3.9]上的零點。

解決方法：試位法

程式語言：python

說明：這裡將分別使用兩種程式語言和3種二分法的終止條件來完成試位的求解。

函式影象：

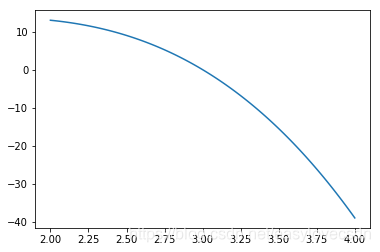
試位的終止條件：

1.區間小於某標準值

2.迴圈次數

3.真實誤差小於某值 |(Xnew - Xold) / Xnew| * 100%

流程圖：

python程式碼

1.迴圈次數

# -*- coding: utf-8 -*-

import math

#最大迴圈次數
maxn = 9999
 
#定義函式f(x)
def f(x):
    return -2.0 * x**3 + 5.0 * x**2 + 9.0
 
#規定兩區間端點
a = 1.0
b = 3.9

#試位法尋求方程解
if (f(a) > 0) :
    for i in range(maxn) : 
        
        fa = math.fabs(f(a))
        fb = math.fabs(f(b))
        
        x = (fa * b + fb * a) / (fa + fb)
        
        if (f(x) == 0) :
            break
        
        if (f(x) > 0) :
            a = x
        else :
            b = x
            
else :
    
    for i in range(maxn) :
        
        fa = math.fabs(f(a))
        fb = math.fabs(f(b))
        
        x = (fa * b + fb * a) / (fa + fb)
        
        if (f(x) == 0) :
            break
        
        if (f(x) > 0) :
            b = x
        else :
            a = x 
    
#輸出結果       
print("f(%.3lf) = %.3lf\n" %(x, f(x)))


            
 

2. 區間長度

# -*- coding: utf-8 -*-

import math

board = 0.5
 
#定義函式f(x)
def f(x):
    return -2.0 * x**3 + 5.0 * x**2 + 9.0
 
#規定兩區間端點
a = 1.0
b = 3.9

#試位法尋求方程解
if (f(a) > 0) :
    while math.fabs(a - b) > board : 
        
        fa = math.fabs(f(a))
        fb = math.fabs(f(b))
        
        x = (fa * b + fb * a) / (fa + fb)
        
        if (f(x) == 0) :
            break
        
        if (f(x) > 0) :
            a = x
        else :
            b = x
            
else :
    
    while math.fabs(a - b) > board :
        
        fa = math.fabs(f(a))
        fb = math.fabs(f(b))
        
        x = (fa * b + fb * a) / (fa + fb)
        
        if (f(x) == 0) :
            break
        
        if (f(x) > 0) :
            b = x
        else :
            a = x 
    
#輸出結果       
print("f(%.3lf) = %.3lf\n" %(x, f(x)))


            
 

3.真實誤差

# -*- coding: utf-8 -*-

import math

rate = 0.000001
 
#定義函式f(x)
def f(x):
    return -2.0 * x**3 + 5.0 * x**2 + 9.0
 
#規定兩區間端點
a = 1.0
b = 3.9

err = 0x3f3f3f3f

#試位法尋求方程解
if (f(a) > 0) :
    while err > rate : 
        
        fa = math.fabs(f(a))
        fb = math.fabs(f(b))
        
        x = (fa * b + fb * a) / (fa + fb)
        
        if (f(x) == 0) :
            break
        
        if (f(x) > 0) :
            err = math.fabs(x - a) / a
            a = x
        else :
            err = math.fabs(x - b) / b
            b = x
            
else :
    
    while err > rate :
        
        fa = math.fabs(f(a))
        fb = math.fabs(f(b))
        
        x = (fa * b + fb * a) / (fa + fb)
        
        if (f(x) == 0) :
            break
        
        if (f(x) > 0) :
            err = math.fabs(x - b) / b
            b = x
        else :
            err = math.fabs(x - a) / a
            a = x 
    
#輸出結果       
print("f(%.3lf) = %.3lf\n" %(x, f(x)))