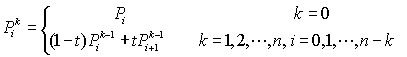2. 程式人生 > >自定義檢視-貝塞爾曲線

自定義檢視-貝塞爾曲線

阿新 • • 發佈：2018-12-23

1.貝塞爾曲線

以下公式中：
B(t)為t時間下 點的座標；
P0為起點,Pn為終點,Pi為控制點

一階貝塞爾曲線(線段)：
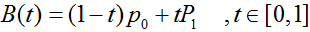
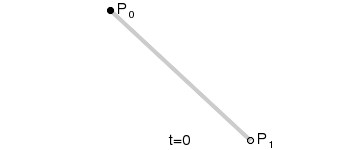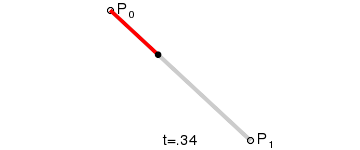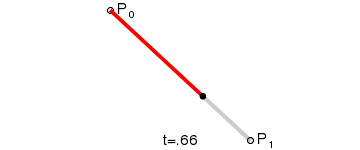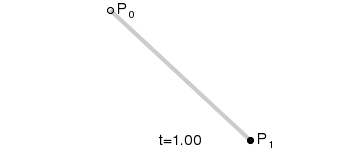
這裡寫圖片描述

這裡寫圖片描述
意義：由 P0 至 P1 的連續點， 描述的一條線段

二階貝塞爾曲線(拋物線)：

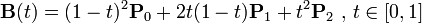
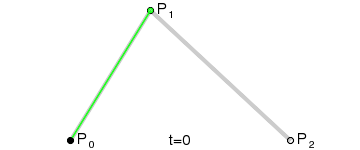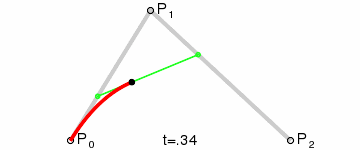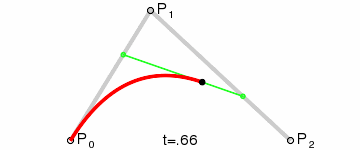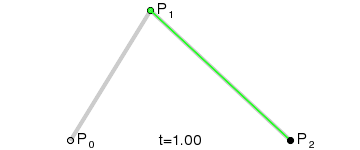
這裡寫圖片描述

這裡寫圖片描述

原理：由 P0 至 P1 的連續點 Q0，描述一條線段。
由 P1 至 P2 的連續點 Q1，描述一條線段。
由 Q0 至 Q1 的連續點 B(t)，描述一條二次貝塞爾曲線。

經驗：P1-P0為曲線在P0處的切線。

三階貝塞爾曲線:

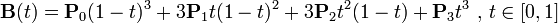
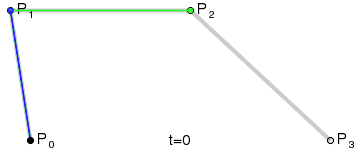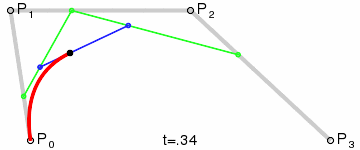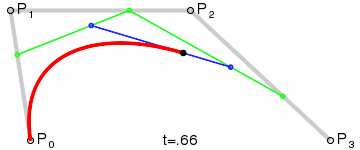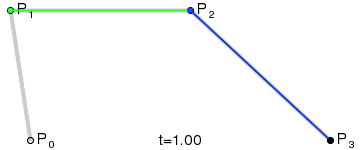
這裡寫圖片描述

這裡寫圖片描述

通用公式：
這裡寫圖片描述

高階貝塞爾曲線：

4階曲線：
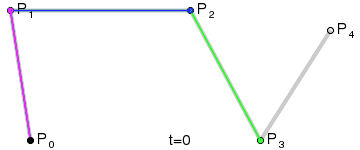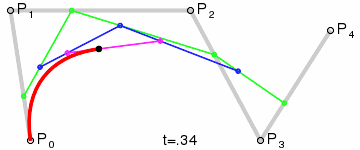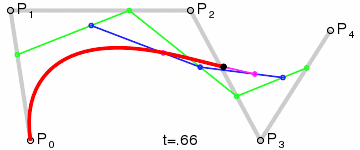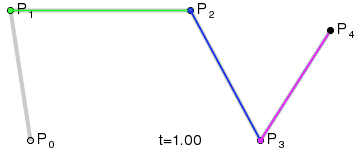
這裡寫圖片描述

5階曲線：
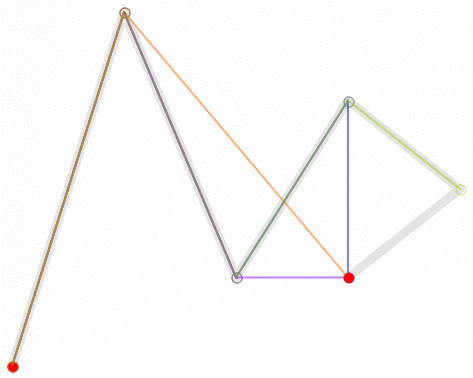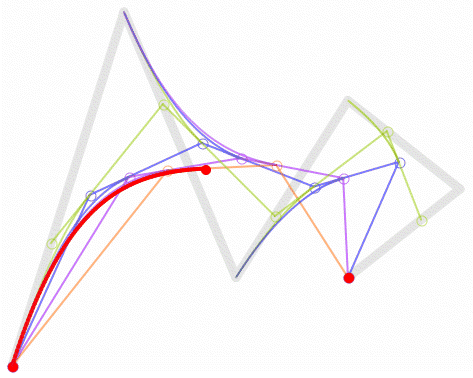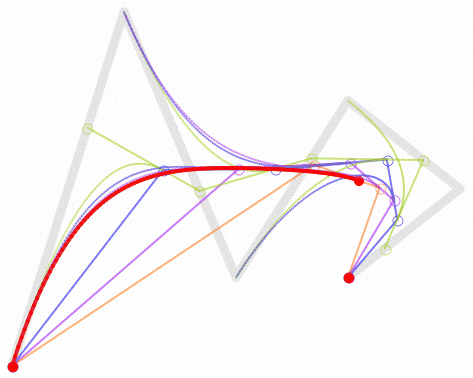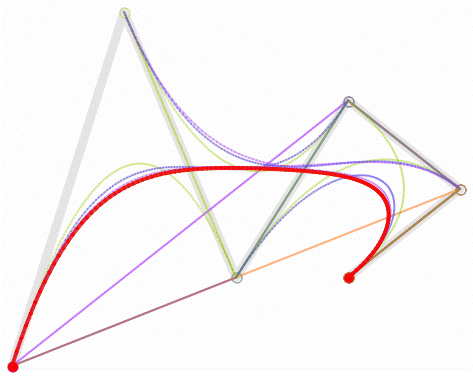
這裡寫圖片描述

1.1.生成貝塞爾曲線-迭代法

下面我們用程式碼來生成貝塞爾曲線，來展示如何貝塞爾曲線的生成原理：

package com.che.testapp.view;

import android.animation.FloatEvaluator;
import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import
 
 android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.View;
import android.view.animation.LinearInterpolator;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;

/**
 * 生成貝塞爾曲線-迭代法
 * <p/>
 * 作者：余天然 on 16/6/14 下午2:10
 */
 

public class BezierGenerater1 extends View {

    private Paint paint;
    private int centerX, centerY;
    private List<PointF> points;
    private FloatEvaluator evaluator;
    private float fraction;
    private Map<Integer, Integer> colors;
    private List<PointF> destPoints;

    public BezierGenerater1(Context context, AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    private void init() {
        paint = new Paint();
        paint.setAntiAlias(true);
        paint.setStyle(Paint.Style.STROKE);
        evaluator = new FloatEvaluator();
        startAnim();
    }

    //初始化資料點和控制點的位置
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        centerX = w / 2;
        centerY = h / 2;
        points = new ArrayList<>();
        points.add(new PointF(centerX - 150, centerY));
        points.add(new PointF(centerX - 50, centerY - 300));
        points.add(new PointF(centerX + 50, centerY + 300));
        points.add(new PointF(centerX + 150, centerY));
        colors = new HashMap<>();
        for (int i = 0; i < points.size(); i++) {
            colors.put(i, getRanColor());
        }
        destPoints = new ArrayList<>();
        destPoints.add(points.get(0));
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        //靜態的
        drawPoint(canvas, points, Color.BLACK);
        drawLine(canvas, points, Color.GRAY);
        //動態的
        List<PointF> subData = getSubData(points, fraction);
        drawData(canvas, subData, fraction);
    }

    // 繪製資料點
    private void drawPoint(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(20);
        for (int i = 0; i < data.size(); i++) {
            PointF pointF = data.get(i);
            canvas.drawPoint(pointF.x, pointF.y, paint);
        }
    }

    //繪製基準線
    private void drawLine(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(4);
        for (int i = 0; i < data.size() - 1; i++) {
            PointF start = data.get(i);
            PointF end = data.get(i + 1);
            canvas.drawLine(start.x, start.y, end.x, end.y, paint);
        }
    }

    //繪製路徑
    private void drawPath(Canvas canvas, List<PointF> data) {
        Path path = new Path();
        PointF start = data.get(0);
        path.moveTo(start.x, start.y);
        for (int i = 1; i < data.size() - 1; i++) {
            PointF point = data.get(i);
            path.lineTo(point.x, point.y);
        }
        paint.setColor(Color.RED);
        paint.setStrokeWidth(4);
        canvas.drawPath(path, paint);
    }

    //迭代繪製集合
    private void drawData(Canvas canvas, List<PointF> data, float fraction) {
        if (data.size() == 1) {
            drawPoint(canvas, data, Color.BLACK);
            destPoints.add(data.get(0));
            drawPath(canvas, destPoints);
        } else {
            drawLine(canvas, data, colors.get(data.size() - 1));
            //迭代
            List<PointF> subData = getSubData(data, fraction);
            drawData(canvas, subData, fraction);
        }
    }

    private void startAnim() {
        ValueAnimator animator = ValueAnimator.ofFloat(0, 100);
        animator.setInterpolator(new LinearInterpolator());
        animator.setDuration(5000);
        animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
            @Override
            public void onAnimationUpdate(ValueAnimator animation) {
                fraction = animation.getAnimatedFraction();
                invalidate();
            }

        });
        animator.start();
    }

    //生成隨機顏色
    private int getRanColor() {
        return 0xff000000 | new Random().nextInt(0x00ffffff);
    }

    //獲取子資料來源
    private List<PointF> getSubData(List<PointF> data, float fraction) {
        List<PointF> subData = new ArrayList<>();
        for (int i = 0; i < data.size() - 1; i++) {
            PointF start = data.get(i);
            PointF end = data.get(i + 1);
            float x = evaluator.evaluate(fraction, start.x, end.x);
            float y = evaluator.evaluate(fraction, start.y, end.y);
            subData.add(new PointF(x, y));
        }
        return subData;
    }
}

1.2.生成貝塞爾曲線-De Casteljau演算法

package com.che.testapp.view;

import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.View;
import android.view.animation.LinearInterpolator;

import java.util.ArrayList;
import java.util.List;

/**
 * 生成貝塞爾曲線-De Casteljau演算法
 * <p/>
 * 作者：余天然 on 16/6/14 下午2:10
 */
public class BezierGenerater2 extends View {

    private Paint paint;
    private int centerX, centerY;
    private List<PointF> points;
    private float fraction;
    private List<PointF> destPoints;

    public BezierGenerater2(Context context, AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    private void init() {
        paint = new Paint();
        paint.setAntiAlias(true);
        paint.setStyle(Paint.Style.STROKE);
    }

    //初始化資料點和控制點的位置
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        centerX = w / 2;
        centerY = h / 2;
        points = new ArrayList<>();
        points.add(new PointF(centerX - 150, centerY));
        points.add(new PointF(centerX - 50, centerY - 300));
        points.add(new PointF(centerX + 50, centerY + 300));
        points.add(new PointF(centerX + 150, centerY));
        destPoints = new ArrayList<>();
        destPoints.add(points.get(0));
        startAnim();
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        //靜態的
        drawPoint(canvas, points, Color.BLACK);
        drawLine(canvas, points, Color.GRAY);
        //動態的
        drawPath(canvas, destPoints);
    }

    // 繪製資料點
    private void drawPoint(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(20);
        for (int i = 0; i < data.size(); i++) {
            PointF pointF = data.get(i);
            canvas.drawPoint(pointF.x, pointF.y, paint);
        }
    }

    //繪製基準線
    private void drawLine(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(4);
        for (int i = 0; i < data.size() - 1; i++) {
            PointF start = data.get(i);
            PointF end = data.get(i + 1);
            canvas.drawLine(start.x, start.y, end.x, end.y, paint);
        }
    }

    //繪製路徑
    private void drawPath(Canvas canvas, List<PointF> data) {
        Path path = new Path();
        PointF start = data.get(0);
        path.moveTo(start.x, start.y);
        for (int i = 1; i < data.size() - 1; i++) {
            PointF point = data.get(i);
            path.lineTo(point.x, point.y);
        }
        paint.setColor(Color.RED);
        paint.setStrokeWidth(4);
        canvas.drawPath(path, paint);
    }

    private void startAnim() {
        ValueAnimator animator = ValueAnimator.ofFloat(0, 100);
        animator.setInterpolator(new LinearInterpolator());
        animator.setDuration(5000);
        animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
            @Override
            public void onAnimationUpdate(ValueAnimator animation) {
                fraction = animation.getAnimatedFraction();
                PointF pointF = deCasteljau(fraction, points);
                destPoints.add(pointF);
                invalidate();
            }
        });
        animator.start();
    }

    //深複製
    private List<PointF> copyData(List<PointF> points) {
        List<PointF> data = new ArrayList<>();
        for (int i = 0; i < points.size(); i++) {
            PointF point = points.get(i);
            data.add(new PointF(point.x, point.y));
        }
        return data;
    }

    //De Casteljau演算法
    public PointF deCasteljau(float fraction, List<PointF> points) {
        List<PointF> data = copyData(points);
        final int n = data.size();
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < n - i; j++) {
                data.get(j).x = (1 - fraction) * data.get(j).x + fraction * data.get(j + 1).x;
                data.get(j).y = (1 - fraction) * data.get(j).y + fraction * data.get(j + 1).y;
            }
        }
        return data.get(0);
    }

}

1.3.二階貝塞爾曲線

上面只是展示了貝塞爾曲線是如何生成的，但是實際上，我們使用的時候，是不必我們自己去生成的，直接呼叫系統api即可，path的quadTo，cubicTo就分別是二階和三階的貝塞爾曲線。至於更高階的，一般用不到，就算真的需要的，用N個三階的疊加即可。

package com.che.testapp.view;

import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;

/**
 * 二階貝塞爾曲線
 * <p/>
 * 兩個資料點和一個控制點
 * 公式：B(t) = (1 - t)^2 * P0 + 2t * (1 - t) * P1 + t^2 * P2, t ∈ [0,1]
 * 作者：余天然 on 16/6/14 上午10:27
 */
public class Bezier2 extends View {
    private Paint paint;
    private int centerX, centerY;
    private PointF start, end, control;

    public Bezier2(Context context, AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    private void init() {
        paint = new Paint();
        paint.setAntiAlias(true);
        paint.setStyle(Paint.Style.STROKE);

        start = new PointF(0, 0);
        end = new PointF(0, 0);
        control = new PointF(0, 0);
    }

    //初始化資料點和控制點的位置
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        centerX = w / 2;
        centerY = h / 2;
        start.x = centerX - 200;
        start.y = centerY;
        end.x = centerX + 200;
        end.y = centerY;
        control.x = centerX;
        control.y = centerY - 100;
    }

    //根據觸控位置更新控制點，並提示重繪
    @Override
    public boolean onTouchEvent(MotionEvent event) {
        control.x = event.getX();
        control.y = event.getY();
        invalidate();
        return true;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        drawPoint(canvas);
        drawGuideLine(canvas);
        drawBezierCurve(canvas);
    }

    // 繪製資料點和控制點
    private void drawPoint(Canvas canvas) {
        paint.setColor(Color.GRAY);
        paint.setStrokeWidth(20);
        canvas.drawPoint(start.x, start.y, paint);
        canvas.drawPoint(end.x, end.y, paint);
        canvas.drawPoint(control.x, control.y, paint);
    }

    //繪製輔助線
    private void drawGuideLine(Canvas canvas) {
        paint.setStrokeWidth(4);
        canvas.drawLine(start.x, start.y, control.x, control.y, paint);
        canvas.drawLine(control.x, control.y, end.x, end.y, paint);
    }

    //繪製貝塞爾曲線
    private void drawBezierCurve(Canvas canvas) {
        paint.setColor(Color.RED);
        paint.setStrokeWidth(4);
        Path path = new Path();
        path.moveTo(start.x, start.y);
        path.quadTo(control.x, control.y, end.x, end.y);
        canvas.drawPath(path, paint);
    }
}

1.4.三階貝塞爾曲線

package com.che.testapp.view;

import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;

import java.util.ArrayList;
import java.util.List;

/**
 * 三階貝塞爾曲線
 * <p/>
 * 2個數據點和2個控制點
 * 公式：B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3 代
 * 作者：余天然 on 16/6/14 上午10:27
 */
public class Bezier3 extends View {

    private Paint paint;
    private int centerX, centerY;
    private List<PointF> points;

    public Bezier3(Context context, AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    private void init() {
        paint = new Paint();
        paint.setAntiAlias(true);
        paint.setStyle(Paint.Style.STROKE);
    }

    //初始化資料點和控制點的位置
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        centerX = w / 2;
        centerY = h / 2;
        points = new ArrayList<>();
        points.add(new PointF(centerX - 150, centerY));
        points.add(new PointF(centerX - 50, centerY - 300));
        points.add(new PointF(centerX + 50, centerY + 300));
        points.add(new PointF(centerX + 150, centerY));
    }

    //根據觸控位置更新控制點，並提示重繪
    @Override
    public boolean onTouchEvent(MotionEvent event) {
        PointF control = new PointF(0, 0);
        control.x = event.getX();
        control.y = event.getY();

        double distance1 = getDistance(control, points.get(1));
        double distance2 = getDistance(control, points.get(2));

        if (distance1 < distance2) {
            points.set(1, control);
        } else {
            points.set(2, control);
        }
        invalidate();
        return true;
    }


    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        drawPoint(canvas, points, Color.BLACK);
        drawLine(canvas, points, Color.GRAY);
        drawBezierCurve(canvas);
    }

    // 繪製資料點
    private void drawPoint(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(20);
        for (int i = 0; i < data.size(); i++) {
            PointF pointF = data.get(i);
            canvas.drawPoint(pointF.x, pointF.y, paint);
        }
    }

    //繪製基準線
    private void drawLine(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(4);
        for (int i = 0; i < data.size() - 1; i++) {
            PointF start = data.get(i);
            PointF end = data.get(i + 1);
            canvas.drawLine(start.x, start.y, end.x, end.y, paint);
        }
    }

    //繪製貝塞爾曲線
    private void drawBezierCurve(Canvas canvas) {
        paint.setColor(Color.RED);
        paint.setStrokeWidth(4);
        Path path = new Path();
        path.moveTo(points.get(0).x, points.get(0).y);
        path.cubicTo(points.get(1).x, points.get(1).y, points.get(2).x, points.get(2).y, points.get(3).x, points.get(3).y);
        canvas.drawPath(path, paint);
    }

    //獲取兩點的距離
    private double getDistance(PointF start, PointF end) {
        return Math.sqrt((end.y - start.y) * (end.y - start.y) + (end.x - start.x) * (end.x - start.x));
    }
}

1.5.用貝塞爾曲線擬合圓形

四段3階貝塞爾曲線
每一段擬合90度扇形
這裡寫圖片描述
這裡寫圖片描述

公式：B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3

顯然，當t=0.5的時候，應該正好在45度的位置上，於是：
sin(pi/4) = 0.125(3x1 - 2) + 0.25(3 - 6x1 ) + 0.5(3x1 )
解出x1=0.55228475或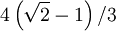這裡寫圖片描述
根據對稱性，可得y1=x1;

package com.che.testapp.view;

import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;

import java.util.ArrayList;
import java.util.List;

/**
 * 貝塞爾曲線-擬合圓形
 * <p/>
 * 作者：余天然 on 16/6/14 上午10:27
 */
public class BezierCircle extends View {

    private Paint paint;
    private int centerX, centerY;
    private List<PointF> points;
    private float magicNumber = 0.55228475f;//(4*(pow(2,1/2)-1)/3
    private float radius = 200;

    public BezierCircle(Context context, AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    private void init() {
        paint = new Paint();
        paint.setAntiAlias(true);
        paint.setStyle(Paint.Style.STROKE);
    }

    //初始化資料點和控制點的位置
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        centerX = w / 2;
        centerY = h / 2;
        points = new ArrayList<>();
        points.add(new PointF(0, radius));
        points.add(new PointF(radius * magicNumber, radius));
        points.add(new PointF(radius, radius * magicNumber));
        points.add(new PointF(radius, 0));
    }

    //根據觸控位置更新控制點，並提示重繪
    @Override
    public boolean onTouchEvent(MotionEvent event) {
        PointF control = new PointF(0, 0);
        control.x = event.getX()-centerX;
        control.y = event.getY()-centerY;

        double distance1 = getDistance(control, points.get(1));
        double distance2 = getDistance(control, points.get(2));

        if (distance1 < distance2) {
            points.set(1, control);
        } else {
            points.set(2, control);
        }
        invalidate();
        return true;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.save();
        canvas.translate(centerX, centerY);
        drawSector(canvas, 0);
        drawSector(canvas, 90);
        drawSector(canvas, 180);
        drawSector(canvas, 270);
        canvas.restore();
    }

    //繪製90度扇形
    private void drawSector(Canvas canvas, float degree) {
        canvas.save();
        canvas.rotate(degree);
        drawPoint(canvas, points, Color.BLACK);
        drawLine(canvas, points, Color.GRAY);
        drawBezierCurve(canvas);
        canvas.restore();
    }

    // 繪製資料點
    private void drawPoint(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(20);
        for (int i = 0; i < data.size(); i++) {
            PointF pointF = data.get(i);
            canvas.drawPoint(pointF.x, pointF.y, paint);
        }
    }

    //繪製基準線
    private void drawLine(Canvas canvas, List<PointF> data, int color) {
        paint.setColor(color);
        paint.setStrokeWidth(4);
        for (int i = 0; i < data.size() - 1; i++) {
            PointF start = data.get(i);
            PointF end = data.get(i + 1);
            canvas.drawLine(start.x, start.y, end.x, end.y, paint);
        }
    }

    //繪製貝塞爾曲線
    private void drawBezierCurve(Canvas canvas) {
        paint.setColor(Color.RED);
        paint.setStrokeWidth(4);
        Path path = new Path();
        path.moveTo(points.get(0).x, points.get(0).y);
        path.cubicTo(points.get(1).x, points.get(1).y, points.get(2).x, points.get(2).y, points.get(3).x, points.get(3).y);
        canvas.drawPath(path, paint);
    }

    //獲取兩點的距離
    private double getDistance(PointF start, PointF end) {
        return Math.sqrt((end.y - start.y) * (end.y - start.y) + (end.x - start.x) * (end.x - start.x));
    }
}

2.自定義檢視

貝塞爾曲線就是PS裡面的魔棒工具，UI上的很多曲線，其實都是用貝塞爾曲線畫的，既然如此，我們只需要知道UI是怎麼畫的，讓她標註好資料點的位置，那我們就可以原樣畫出UI效果了。

貝塞爾曲線的用處，就是動態繪製平滑曲線！
並且可以實時控制曲線狀態，並可以通過改變控制點的狀態實時讓曲線進行平滑的狀態變化。

2.1.氣泡拖拽效果

效果圖：
這裡寫圖片描述

這裡寫圖片描述

上面的圖是盜來的，因為我還不會在手機上錄製gif,下面的我的demo的截圖：
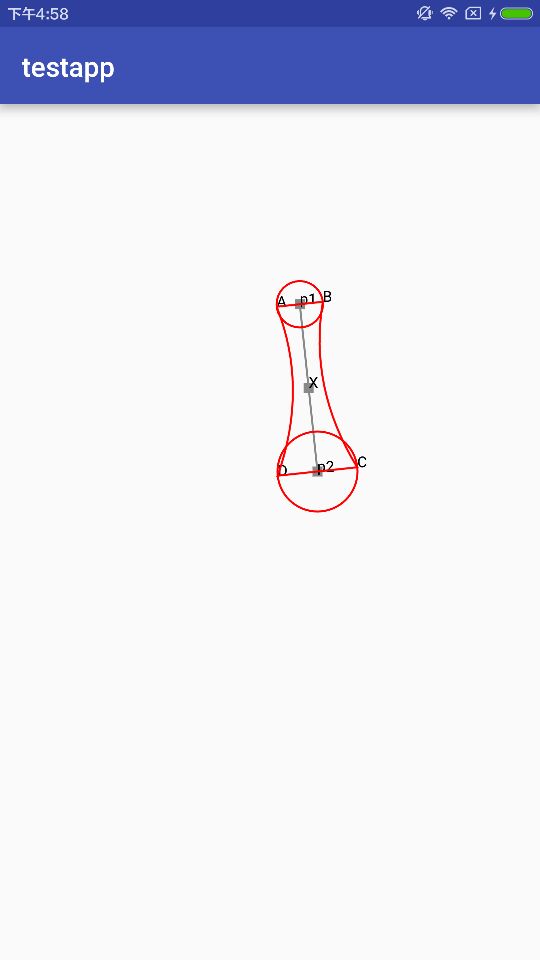
這裡寫圖片描述

這裡:
p1是初始圓的圓心，p2是拖動圓的圓心
X是p1p2線段的中點
AB：與p1p2線段垂直，長度為初始圓的直徑
CD：與p1p2線段垂直，長度為拖動圓的直徑

繪製流程：
1.繪製p1和p2的圓形
2.根據A，X，D繪製一條2階貝塞爾曲線
3.根據B，X，C繪製另一條2階貝塞爾曲線
4.設定path的模式為填充模式

package com.che.testapp.view;

import android.animation.FloatEvaluator;
import android.animation.ValueAnimator;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.PointF;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;
import android.view.animation.OvershootInterpolator;

/**
 * 貝塞爾曲線-氣泡拖拽
 * <p/>
 * 二條2階貝塞爾曲線
 * 作者：余天然 on 16/6/14 上午10:27
 */
public class BezierDraggableFlag extends View {
    private Paint paint;
    private int raduis = 40;//氣泡的半徑
    private double distance;//記錄拉動的距離
    private double raduisTmp;//臨時的半徑
    private int maxDistance = 800;//拉斷的距離
    private PointF p1, p2;//圓心
    private PointF pA, pB, pC, pD, pX;//控制點

    private double distanceBackup;
    private PointF p2Backup;

    public BezierDraggableFlag(Context context, AttributeSet attrs) {
        super(context, attrs);
        init();
    }

    //初始化圓心的位置
    private void init() {
        paint = new Paint();
        paint.setAntiAlias(true);

        p1 = new PointF(600, 400);
        p2 = new PointF(600, 400);
    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()) {
            case MotionEvent.ACTION_DOWN:
                break;
            case MotionEvent.ACTION_MOVE:
                p2.x = event.getX();
                p2.y = event.getY();
                distance = PointUtil.getDistance(p1, p2);
                invalidate();
                break;
            case MotionEvent.ACTION_UP:
                if (distance < maxDistance) {
                    p2Backup = new PointF(p2.x, p2.y);
                    distanceBackup = distance;
                    startAnim();
                }
                break;
        }
        return true;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        if (distance < maxDistance) {
            calculatePoint();
            drawBefore(canvas);
        } else {
            drawAfter(canvas);
        }
    }

    //計算控制點的位置
    private void calculatePoint() {
        double raduisScale = 1 - distance / maxDistance;
        raduisTmp = raduis * raduisScale;

        pA = PointUtil.getRotatePoint(p1, p2, raduisTmp, Math.PI / 2);
        pB = PointUtil.getRotatePoint(p1, p2, raduisTmp, -Math.PI / 2);
        pC = PointUtil.getRotatePoint(p2, p1, raduis, -Math.PI / 2);
        pD = PointUtil.getRotatePoint(p2, p1, raduis, Math.PI / 2);
        pX = PointUtil.getCenterPoint(p1, p2);
    }

    //拉斷之後的繪製
    private void drawAfter(Canvas canvas) {
        paint.setColor(Color.RED);
        paint.setStyle(Paint.Style.FILL);
        paint.setStrokeWidth(4);
        canvas.drawCircle(p2.x, p2.y, raduis, paint);
    }

    //拉斷之前的繪製
    private void drawBefore(Canvas canvas) {
        //端點
//        paint.setColor(Color.GRAY);
//        paint.setStyle(Paint.Style.STROKE);
//        paint.setStrokeWidth(20);
//        canvas.drawPoint(p1.x, p1.y, paint);
//        canvas.drawPoint(p2.x, p2.y, paint);
//        canvas.drawPoint(pX.x, pX.y, paint);

        //輔助線
        paint.setColor(Color.GRAY);
        paint.setStyle(Paint.Style.STROKE);
        paint.setStrokeWidth(4);
        canvas.drawLine(p1.x, p1.y, p2.x, p2.y, paint);

        //文字
//        paint.setColor(Color.BLACK);
//        paint.setStyle(Paint.Style.FILL);
//        paint.setStrokeWidth(2);
//        paint.setTextSize(30);
//        canvas.drawText("A", pA.x, pA.y, paint);
//        canvas.drawText("B", pB.x, pB.y, paint);
//        canvas.drawText("C", pC.x, pC.y, paint);
//        canvas.drawText("D", pD.x, pD.y, paint);
//        canvas.drawText("X", pX.x, pX.y, paint);
//        canvas.drawText("p1", p1.x, p1.y, paint);
//        canvas.drawText("p2", p2.x, p2.y, paint);

        //圓形
        paint.setColor(Color.RED);
        paint.setStyle(Paint.Style.FILL);
        paint.setStrokeWidth(4);
        canvas.drawCircle(p1.x, p1.y, (float) raduisTmp, paint);
        canvas.drawCircle(p2.x, p2.y, raduis, paint);

        //貝塞爾曲線
        paint.setColor(Color.RED);
        paint.setStyle(Paint.Style.FILL);
        paint.setStrokeWidth(4);
        Path path = new Path();
        path.moveTo(pA.x, pA.y);
        path.quadTo(pX.x, pX.y, pD.x, pD.y);
        path.lineTo(pC.x, pC.y);
        path.quadTo(pX.x, pX.y, pB.x, pB.y);
        path.lineTo(pA.x, pA.y);
        canvas.drawPath(path, paint);
    }


    //放開之後，如果沒有拉斷，就恢復初始狀態
    private void startAnim() {
        final FloatEvaluator evaluator = new FloatEvaluator();
        ValueAnimator animator = ValueAnimator.ofFloat(0, 100);
        animator.setInterpolator(new OvershootInterpolator());
        animator.setDuration(100);
        animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
            @Override
            public void onAnimationUpdate(ValueAnimator animation) {
                float fraction = animation.getAnimatedFraction();
                p2.x = evaluator.evaluate(fraction, p2Backup.x, p1.x);
                p2.y = evaluator.evaluate(fraction, p2Backup.y, p1.y);
                distance = evaluator.evaluate(fraction, distance, 0);
                invalidate();
            }

        });
        animator.start();
    }


}

這裡用到了一個工具類：

package com.che.testapp.view;

import android.graphics.PointF;

/**
 * 點計算工具類
 * <p/>
 * 作者：余天然 on 16/6/15 下午2:33
 */
public class PointUtil {

    //獲取旋轉後的點
    public static PointF getRotatePoint(PointF p1, PointF p2, double raduis, double radians) {
        double oldRadians = getPointDegree(p1, p2);
        double newRadians = oldRadians + radians;
        float x = (float) (raduis * Math.cos(newRadians));
        float y = (float) (raduis * Math.sin(newRadians));
        return new PointF(p1.x + x, p1.y + y);
    }

    //獲取中間的點
    public static PointF getCenterPoint(PointF p1, PointF p2) {
        float x = (p1.x + p2.x) / 2;
        float y = (p1.y + p2.y) / 2;
        return new PointF(x, y);
    }

    //獲取兩點的角度-返

相關推薦

自定義檢視-貝塞爾曲線

1.貝塞爾曲線 以下公式中： B(t)為t時間下 點的座標； P0為起點,Pn為終點,Pi為控制點 一階貝塞爾曲線(線段)： 意義：由 P0 至 P1 的連續點， 描述的一條線段 二階貝塞爾曲線(拋物線)：

Android自定義View——貝塞爾曲線實現水波紋進度球

效果圖 原理分析 首先需要了解的水波紋實現效果，可以在部落格的自定義View專題找到，其實現原理如下 利用貝塞爾曲線繪製螢幕外和螢幕內的sin曲線 利用path將sin曲線的左下角和右下角連線起來成為一塊區域 通過不斷的平移sin曲線，然後平移完

Android 自定義Path貝塞爾曲線View實踐——旋轉的花朵

開發十年，就只剩下這套架構體系了！ >>>   

Android -- 自定義ViewGroup+貝塞爾+屬性動畫實現仿QQ點贊效果

private void init(final Context context) { mStarDrawable = new ArrayList<>(); mInterpolators = new ArrayList<>(); mSt

自定義View,貝賽爾曲線實現水波紋進度條

最終的效果：  思路就是在onDraw()中畫一些內容，主要方法有這些： /** * 剪裁圓形區域 */ clipCircle(canvas); /** * 畫圓邊線 */ drawCircle(canvas); /** * 畫波浪線 */ drawWave(

安卓自定義View進階-Path之貝塞爾曲線

在上一篇文章Path之基本操作中我們瞭解了Path的基本使用方法，本次瞭解Path中非常非常非常重要的內容-貝塞爾曲線。 一.Path常用方法表 為了相容性(偷懶) 本表格中去除了在API21(即安卓版本5.0)以上

025.自定義View中應用貝塞爾曲線

之前一直看QQ的未讀訊息拖拽消失設計得很好，我一直覺得那個設計很好，他們的UI是真心強，於是，我也一直想寫個一樣的玩意來玩玩。最近剛好在複習View相關的知識，就拿這個來練手，下面先來看實現的效果圖： 這是我希望實現的效果，這個效果的實現在第二個圖能看出一點端倪。這裡面的曲線繪製，

自定義view，貝塞爾曲線實現水波紋效果的動畫

作為一名碼農，除了用基本的姿勢去搬磚，還應該get一些炫酷的技能，用高逼格的姿態去搬磚。而貝塞爾曲線無疑是炫酷技能之一。 簡介： Bézier curve(貝塞爾曲線)是應用於二維圖形應用程式的數學曲線。 曲線定義：起始點、終止點（也稱錨點）、控制點。通過調整控

自定義view(三) 貝塞爾曲線 水波紋效果實現

目錄 前言 api分析 水波紋效果 前言 在上面的部落格中說了path的繪製，path繪製， 介紹了除了貝塞爾曲線的其他情況。 在這裡單獨介紹一下貝塞爾曲線。貝塞爾曲線是應用於二維圖形應用程式的數學曲線。一般的向量圖形軟體通過它來精確畫出曲線，

自定義控制元件之二階貝塞爾曲線方法詳解

前言：先膜拜一下啟艦大神，本想自己寫一篇關於貝塞爾曲線的文章，但無奈此大神寫的太6了 ，所以直接轉載 相關文章：《Android自定義控制元件三部曲文章索引》: http://blog.csdn.net/harvic880925/article/details/50995268從

Android自定義View進階 - 貝塞爾曲線

                Path之貝塞爾曲線 作者微博: @GcsSloop 【本系列相關文章】 在

Android自定義View阻尼動畫&貝塞爾曲線的實現

效果圖：直接上程式碼啦：package com.example.administrator.myapplication.customview; import android.animation.Animator; import android.animation.Anim

安卓自定義 View 進階：貝塞爾曲線

在上一篇文章Path之基本圖形中我們瞭解了Path的基本使用方法，本次瞭解Path中非常非常非常重要的內容-貝塞爾曲線。 一.Path常用方法表 為了相容性(偷懶) 本表格中去除了在API21(即安卓版本5.0)以上才新增的方法。忍不住吐槽一下，為啥看起來有些順手就能寫的

Android 自定義View高階特效，神奇的貝塞爾曲線

初始化引數 private static final String TAG = "BIZIER"; private static final int LINEWIDTH = 5; private static final int POINTWIDTH = 10; private Context mContex

Android自定義view進階-- 神奇的貝塞爾曲線

上一篇介紹了自定義view需要知道的基本函式。新開一篇獻給借給我vpn的深圳_奮鬥小哥。 轉載請註明出處：http://blog.csdn.net/wingichoy/article/details/50492828 今天給大家介紹一個非常神奇的曲線，貝塞爾曲線。相信大

讓一個檢視在隨著貝塞爾曲線的變化上動起來

具體demo@上海-鄧澤淼 1、涉及概念 1）UIDynamicItemCollisionBoundsType 碰撞界限的列舉型別（矩形，橢圓，路徑） 2）CADisplayLink是一個能讓我們以和螢幕重新整理率相同的頻率將內容畫到螢幕上的定時器。我們在應用中建立一個新

Unity遊戲中使用貝塞爾曲線

str net 順序 復雜 讓我 創建 函數 高程 gin 孫廣東 2015.8.15比方在3D rpg遊戲中。我們想設置彈道，不同的軌跡類型！目的:這篇文章的主要目的是要給你關於在遊戲怎樣使用貝塞爾曲線的基本想法。 貝塞爾曲線是最主要的曲線，一般用

貝塞爾曲線實現的購物車添加商品動畫效果

right map 繪制 開始 enter 監聽 idg 過程 protected 效果圖如下： 1.activity_main.xml <?xml version="1.0" encoding="utf-8"?> <RelativeLayout xm

把商品添加到購物車的動畫效果（貝塞爾曲線）

param from mat 位置 hold pos 開始 onclick border 目錄(?)[+] 如圖： 參考： Android補間動畫，屬性動畫實現購物車添加動畫 思路： 確定動畫的起終點 在起終點之間使用二次貝塞爾曲線填充起終點之間的點的軌跡 設置屬

iOS 使用貝塞爾曲線繪制路徑

繪制直線 多邊形 ini rcc 三個點 memory images arc poi 使用貝塞爾曲線繪制路徑 大多數時候，我們在開發中使用的控件的邊框是矩形，或者做一點圓角，是使得矩形的角看起來更加的圓滑。 但是如果我們想要一個不規則的圖形怎麽辦？有人說，叫UI