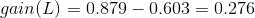歡迎轉載，轉載請註明：本文出自Bin的專欄blog.csdn.net/xbinworld。
技術交流QQ群：433250724，歡迎對演算法、技術、應用感興趣的同學加入。

前面三篇寫了線性迴歸，lasso，和LARS的一些內容，這篇寫一下決策樹這個經典的分類演算法，後面再提一提隨機森林。關於決策樹的內容主要來自於網路上幾個技術部落格，本文中借用的地方我都會寫清楚出處，寫這篇[整理文章]的目的是對決策樹的概念原理、計算方法進行梳理。本文主要參考文獻的[1][2]的圖片和例子。另外，[3]寫的也比較仔細，有程式碼可以參考，可以看看。不過如果只想簡單瞭解一下原理，看本文即可。

決策樹

決策樹（decision tree）是一個樹結構（可以是二叉樹或非二叉樹）。其每個非葉節點表示一個特徵屬性上的測試，每個分支代表這個特徵屬性在某個值域上的輸出，而每個葉節點存放一個類別。使用決策樹進行決策的過程就是從根節點開始，測試待分類項中相應的特徵屬性，並按照其值選擇輸出分支，直到到達葉子節點，將葉子節點存放的類別作為決策結果[1]。

下面先來看一個小例子，看看決策樹到底是什麼概念（這個例子來源於[2]）。

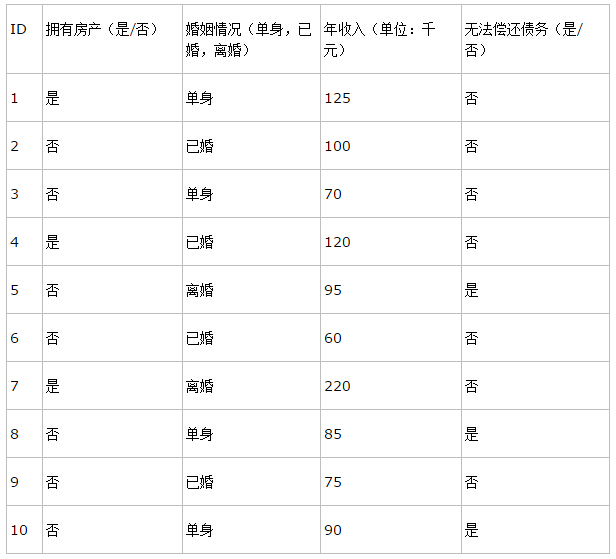
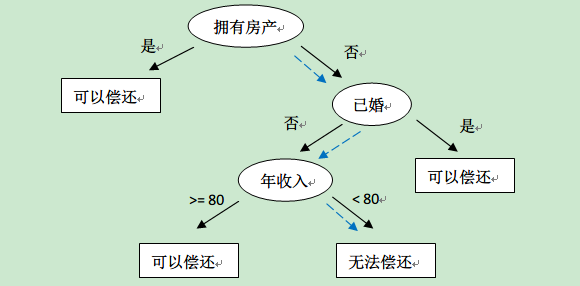
決策樹的訓練資料往往就是這樣的表格形式，表中的前三列（ID不算）是資料樣本的屬性，最後一列是決策樹需要做的分類結果。通過該資料，構建的決策樹如下：

有了這棵樹，我們就可以對新來的使用者資料進行是否可以償還的預測了。

決策樹最重要的是決策樹的構造。所謂決策樹的構造就是進行屬性選擇度量確定各個特徵屬性之間的拓撲結構。構造決策樹的關鍵步驟是分裂屬性。所謂分裂屬性就是在某個節點處按照某一特徵屬性的不同劃分構造不同的分支，其目標是讓各個分裂子集儘可能地“純”。儘可能“純”就是儘量讓一個分裂子集中待分類項屬於同一類別。分裂屬性分為三種不同的情況[1]：
1、屬性是離散值且不要求生成二叉決策樹。此時用屬性的每一個劃分作為一個分支。
2、屬性是離散值且要求生成二叉決策樹。此時使用屬性劃分的一個子集進行測試，按照“屬於此子集”和“不屬於此子集”分成兩個分支。
3、屬性是連續值。此時確定一個值作為分裂點split_point，按照>split_point和<=split_point生成兩個分支。

決策樹的屬性分裂選擇是”貪心“演算法，也就是沒有回溯的。

ID3.5

好了，接下來說一下教科書上提到最多的決策樹ID3.5演算法（是最基本的模型，簡單實用，但是在某些場合下也有缺陷）。

資訊理論中有熵（entropy）的概念，表示狀態的混亂程度，熵越大越混亂。熵的變化可以看做是資訊增益，決策樹ID3演算法的核心思想是以資訊增益度量屬性選擇，選擇分裂後資訊增益最大的屬性進行分裂。

設D為用（輸出）類別對訓練元組進行的劃分，則D的熵表示為：

如果將訓練元組D按屬性A進行劃分，則A對D劃分的期望資訊為：

於是，資訊增益就是兩者的差值：

ID3決策樹演算法就用到上面的資訊增益，在每次分裂的時候貪心選擇資訊增益最大的屬性，作為本次分裂屬性。每次分裂就會使得樹長高一層。這樣逐步生產下去，就一定可以構建一顆決策樹。（基本原理就是這樣，但是實際中，為了防止過擬合，以及可能遇到葉子節點類別不純的情況，需要有一些特殊的trick，這些留到最後講）

OK，借鑑一下[1]中的一個小例子，來看一下資訊增益的計算過程。

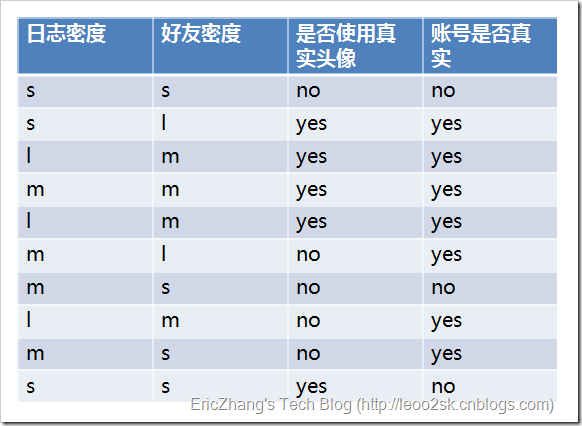
這個例子是這樣的：輸入樣本的屬性有三個——日誌密度（L），好友密度（F），以及是否使用真實頭像（H）；樣本的標記是賬號是否真實yes or no。

然後可以一次計算每一個屬性的資訊增益，比如日緻密度的資訊增益是0.276。

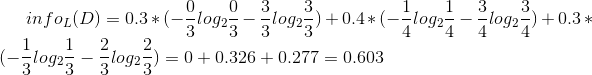
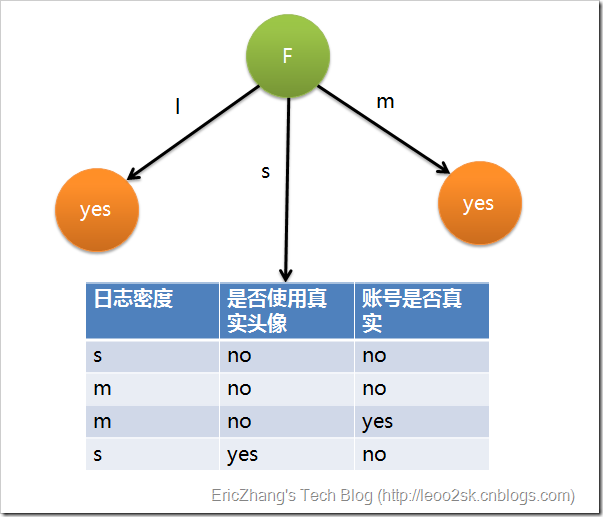
同理可得H和F的資訊增益為0.033和0.553。因為F具有最大的資訊增益，所以第一次分裂選擇F為分裂屬性，分裂後的結果如下圖表示：

上面為了簡便，將特徵屬性離散化了，其實日誌密度和好友密度都是連續的屬性。對於特徵屬性為連續值，可以如此使用ID3演算法：先將D中元素按照特徵屬性排序，則每兩個相鄰元素的中間點可以看做潛在分裂點，從第一個潛在分裂點開始，分裂D並計算兩個集合的期望資訊，具有最小期望資訊的點稱為這個屬性的最佳分裂點，其資訊期望作為此屬性的資訊期望。

C4.5

ID3有一些缺陷，就是選擇的時候容易選擇一些比較容易分純淨的屬性，尤其在具有像ID值這樣的屬性，因為每個ID都對應一個類別，所以分的很純淨，ID3比較傾向找到這樣的屬性做分裂。

C4.5演算法定義了分裂資訊，表示為：

很容易理解，這個也是一個熵的定義，pi=|Dj||D|，可以看做是屬性分裂的熵，分的越多就越混亂，熵越大。定義資訊增益率：

實現trick

這一部分參考[2]
停止條件

決策樹的構建過程是一個遞迴的過程，所以需要確定停止條件，否則過程將不會結束。一種最直觀的方式是當每個子節點只有一種型別的記錄時停止，但是這樣往往會使得樹的節點過多，導致過擬合問題（Overfitting）。另一種可行的方法是當前節點中的記錄數低於一個最小的閥值，那麼就停止分割，將max(P(i))對應的分類作為當前葉節點的分類。

過度擬合

採用上面演算法生成的決策樹在事件中往往會導致過度擬合。也就是該決策樹對訓練資料可以得到很低的錯誤率，但是運用到測試資料上卻得到非常高的錯誤率。過渡擬合的原因有以下幾點：
•噪音資料：訓練資料中存在噪音資料，決策樹的某些節點有噪音資料作為分割標準，導致決策樹無法代表真實資料。
•缺少代表性資料：訓練資料沒有包含所有具有代表性的資料，導致某一類資料無法很好的匹配，這一點可以通過觀察混淆矩陣（Confusion Matrix）分析得出。
•多重比較（Mulitple Comparision）：舉個列子，股票分析師預測股票漲或跌。假設分析師都是靠隨機猜測，也就是他們正確的概率是0.5。每一個人預測10次，那麼預測正確的次數在8次或8次以上的概率為 ，C810∗(0.5)10+C910∗(0.5)10+C1010∗(0.5)10只有5%左右，比較低。但是如果50個分析師，每個人預測10次，選擇至少一個人得到8次或以上的人作為代表，那麼概率為 1−(1−0.0547)50=0.9399，概率十分大，隨著分析師人數的增加，概率無限接近1。但是，選出來的分析師其實是打醬油的，他對未來的預測不能做任何保證。上面這個例子就是多重比較。這一情況和決策樹選取分割點類似，需要在每個變數的每一個值中選取一個作為分割的代表，所以選出一個噪音分割標準的概率是很大的。

優化方案1：修剪枝葉

決策樹過渡擬合往往是因為太過“茂盛”，也就是節點過多，所以需要裁剪（Prune Tree）枝葉。裁剪枝葉的策略對決策樹正確率的影響很大。主要有兩種裁剪策略。

前置裁剪 在構建決策樹的過程時，提前停止。那麼，會將切分節點的條件設定的很苛刻，導致決策樹很短小。結果就是決策樹無法達到最優。實踐證明這中策略無法得到較好的結果。

後置裁剪 決策樹構建好後，然後才開始裁剪。採用兩種方法：1）用單一葉節點代替整個子樹，葉節點的分類採用子樹中最主要的分類；2）將一個字數完全替代另外一顆子樹。後置裁剪有個問題就是計算效率，有些節點計算後就被裁剪了，導致有點浪費。

優化方案2：K-Fold Cross Validation

首先計算出整體的決策樹T，葉節點個數記作N，設i屬於[1,N]。對每個i，使用K-Fold Validataion方法計算決策樹，並裁剪到i個節點，計算錯誤率，最後求出平均錯誤率。（意思是說對每一個可能的i，都做K次，然後取K次的平均錯誤率。）這樣可以用具有最小錯誤率對應的i作為最終決策樹的大小，對原始決策樹進行裁剪，得到最優決策樹。

優化方案3：Random Forest

Random Forest是用訓練資料隨機的計算出許多決策樹，形成了一個森林。然後用這個森林對未知資料進行預測，選取投票最多的分類。實踐證明，此演算法的錯誤率得到了經一步的降低。這種方法背後的原理可以用“三個臭皮匠定一個諸葛亮”這句諺語來概括。一顆樹預測正確的概率可能不高，但是集體預測正確的概率卻很高。RF是非常常用的分類演算法，效果一般都很好。

OK，決策樹就講到這裡，商用的決策樹C5.0瞭解不是很多；還有分類迴歸樹CART也很常用。