在大二第一學期因為興趣原因,自己學習了一些資料分析的演算法,這裡面便包含決策樹,總的來說,學習的情況還是比較良好的,有那個意願自己去學習.現在想想,那時的學習過程還是挺艱辛的,因為其實幾種決策樹,ID3,C4.5,CART之間的區別,當時在網上是有很多說法的,或者說其實很多說法說的都對,但都是答案的一部分,當時查了很久不得其解,比如說有的說CART跟其他兩種的區別在於用GINI屬性來劃分屬性,有的說是因為既可以進行分類也可以進行迴歸，既可以處理離散屬性，也可以處理連續的.其實這些都是正確的,只是有些部落格說的片面了點而已.

現在回過頭來再次學習,一方面由於熟悉的原因,另一方面感覺自己閱讀程式碼的能力還是有所進步的

一. 決策樹介紹

決策樹(Decision Tree）是在已知各種情況發生概率的基礎上，通過構成決策樹來求取淨現值的期望值大於等於零的概率，評價專案風險，判斷其可行性的決策分析方法，是直觀運用概率分析的一種圖解法。由於這種決策分支畫成圖形很像一棵樹的枝幹，故稱決策樹。

二.  原理介紹

決策樹是一種非引數的監督學習方法，它主要用於分類和迴歸。決策樹的目的是構造一種模型，使之能夠從樣本資料的特徵屬性中，通過學習簡單的決策規則——IF THEN

決策樹往往採用的是自上而下的設計方法，每迭代迴圈一次，就會選擇一個特徵屬性進行分叉，直到不能再分叉為止。因此在構建決策樹的過程中，選擇最佳（既能夠快速分類，又能使決策樹的深度小）的分叉特徵屬性是關鍵所在。這種“最佳性”可以用非純度（impurity）進行衡量。如果一個數據集合中只有一種分類結果，則該集合最純，即一致性好；反之有許多分類，則不純，即一致性不好。有許多指標可以定量的度量這種非純度，最常用的有熵，基尼指數（Gini Index）和分類誤差，它們的公式分別為：

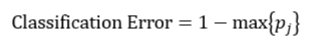
上述所有公式中，值越大，表示越不純，這三個度量之間並不存在顯著的差別。式中

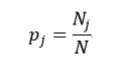
式中N和Nj分別表示集合D中樣本資料的總數和第j個分類的樣本數量。把式4帶入式2中，得到：

目前常用的決策樹的演算法包括ID3（Iterative Dichotomiser 3）、C4.5和CART（ClassificationAnd Regression Tree，分類和迴歸樹）。前兩種演算法主要應用的是基於熵的方法，而第三種應用的是基尼指數的方法。

ID3和C4.5最大的差別在於,分類時的依據,ID3依據資訊增益(基於熵),而C4.5是依據資訊增益率.ID3應用的資訊增益的方法存在一個問題，就是它會更願意選擇那些包括很多種類的特徵屬性，即哪個A中的n多，那麼這個A的資訊增益就可能更大。為此，C4.5使用資訊增益率這一準則來衡量非純度，可以對比一下:

ID3

C4.5

CART決策樹,則主要用了基尼不純度作為分類標準,這是分類樹,而回歸樹,則是用了方差來衡量資料,把適合分類的非純度度量用適合迴歸的非純度度量取代.簡單來說,區分分類樹和迴歸樹,在於分類樹的樣本輸出（即響應值）是類的形式，而回歸樹的樣本輸出是數值的形式.

上面所說的熵和基尼不純度,主要就是決策樹在構建過程中,將資料要按那個屬性進行劃分的依據,總的來說,分類資料總是從無序到有序,但在這個過程中,資料收斂到該演算法能達到的最佳情況下的時間和步驟也不一樣,最佳構建出的決策樹也會有所差異.

三.  學習心得

在我學習之後,我認為在實際學習生活應用中,分類和迴歸,有時還是可以相互轉換的,不是說原本資料是類別,傳入引數就一定是類別,也不一定說原本資料是數值,傳入引數就一定不能是類別,這還是要根據實際情況對資料進行預處理,處理成能夠符合你建立的模型的資料,方可進行模型的訓練.

對了,決策樹中構建樹用到的衡量度,熵和基尼指數,我查了許多資料後,發現,熵和基尼不純度之間的主要區別在於,熵達到峰值的過程要相對慢一些.因此,熵對混亂集合的”判罰”要相對重一些,在現實中,人們對熵的使用更為普遍.

我總結了一下一棵完整的決策樹需要考慮到的問題:

1.當用戶想要檢測一些非常罕見的異常現象的時候，這是非常難辦到的，這是因為訓練可能包含了比異常多得多的正常情況，那麼很可能分類結果就是認為每一個情況都是正常的.為了避免這種情況的出現，我們需要設定先驗概率，這樣異常情況發生的概率就被人為的增加（可以增加到0.5甚至更高），這樣被誤分類的異常情況的權重就會變大，決策樹也能夠得到適當的調整.這一步我記得在樸素貝葉斯演算法裡也曾見到過,足以說明這個問題還是挺容易出現在分類中的.

2.第二個需要解決的問題是，某些樣本缺失了某個特徵屬性，但該特徵屬性又是最佳分叉屬性，那麼如何對該樣本進行分叉呢？目前有幾種方法可以解決該問題，一種是直接把該樣本刪除掉.另一種方法是用各種演算法估計該樣本的缺失屬性值.還有一種方法就是用另一個特徵屬性來替代最佳分叉屬性，該特徵屬性被稱為替代分叉屬性.因此在計算最佳分叉屬性的同時，還要計算該特徵屬性的替代分叉屬性，以防止最佳分叉屬性缺失的情況.

3.過擬合.這是在機器學習演算法中很容易出現的問題,在決策樹中,解決方法就是將複雜的決策樹進行簡化,稱為剪枝，它的目的是去掉一些節點，包括葉節點和中間節點。剪枝常用的方法有預剪枝和後剪枝兩種。預剪枝是在構建決策樹的過程中，提前終止決策樹的生長，從而避免過多的節點的產生。該方法雖然簡單但實用性不強，因為我們很難精確的判斷何時終止樹的生長。後剪枝就是在決策樹構建完後再去掉一些節點。常見後剪枝方法有四種：悲觀錯誤剪枝（PEP）、最小錯誤剪枝（MEP）、代價複雜度剪枝（CCP）和基於錯誤的剪枝（EBP）。CCP演算法能夠應用於CART演算法中.

我覺得吧,剪枝是及其重要的一步,能夠更好地發揮決策樹的優越性,一棵冗雜的樹,儘管實現分類決策成功了,但是效率相比較來說比較低,更重要的是可能出現測試資料沒有代表性的情況.剪枝較好地解決了過擬合的問題,實際應用價值更大.

決策樹,也是非常經典的演算法了,一開始學的時候,是覺得名字看起來挺有趣的,而且資料結構時候學過平衡二叉樹那些,對樹這種結構還是比較熟悉的,結果當時學這個還是有點吃力,主要便在於樹的構建和構建之後的優化操作會需要邏輯思維好一點.

我覺得資料探勘的演算法有些還是很有趣的,經典不代表過時,決策樹也是作為入門資料探勘的很好的演算法學習之一,我覺得很直觀,新手很容易直觀地看出分類的走向,雖然核心演算法還是要下點功夫好好鑽研一下.

當然,以上我的觀點和所列舉的知識點可能還有不恰當或者缺漏的現象,這也是很可能存在的,畢竟我可能學習時間不夠,有一些深層知識點還沒體會到的,還是要繼續努力下去把.