機器學習之決策樹演算法詳解

1-1 基本流程

決策樹是一個有監督分類與迴歸演算法。
決策樹的生成只考慮區域性最優，相對的，決策樹剪枝則考慮全域性最優。

一、概念：

決策樹：是一種樹形結構，其中每個內部節點表示一個屬性上的判斷，每個分支代表一個判斷結果的輸出，最後每個葉節點代表一種分類結果，本質是一顆由多個判斷節點組成的樹。

二、劃分依據：

①熵

物理學上，熵 Entropy 是“混亂” 程度的量度。
系統越有序，熵值越低；系統越混亂或者分散，熵值越高
資訊理論：
1、當系統的有序狀態一致時，資料越集中的地方熵值越小，資料越分散的地方熵值越大。這是從資訊的完整性上進行的描述。
2、當資料量一致時，系統越有序，熵值越低；系統越混亂或者分散，熵值越高。這是從資訊的有序性上進行的描述。

假如事件A的分類劃分是（A1,A2,…,An），每部分發生的概率是(p1,p2,…,pn)，那資訊熵定義為公式如下：

E n t (A) = - \sum_{k = 1}^{n} p_{k} l o g_{2} p_{k}

二分法：
如果有32個球隊，準確的資訊量應該是：
H = -（p1 * logp1 + p2 * logp2 + … + p32 * logp32），其中 p1, …, p32 分
別是這 32 支球隊奪冠的概率。當每支球隊奪冠概率相等都是 1/32 的時：H = -（32 * 1/32 * log1/32） = 5 每個事件概率相同時，熵最大，這件事越不確定。

②特徵選擇–資訊增益及增益率

資訊增益：以某特徵劃分資料集前後的熵的差值。熵可以表示樣本集合的不確定性，熵越大，樣本的不確定性就越大。因此可以使用劃分前後集合熵的差值來衡量使用當前特徵對於樣本集合D劃分效果的好壞。
資訊增益 = entroy(前) - entroy(後)
資訊增益公式如下：
D：為樣本集
Ent(D):整體熵
a:離散型屬性
v: 是a屬性裡可能的取值節點
D^v：第v個分支節點包含了D中所有在屬性a上取值為a\^v的樣本

資訊增益越大，不確定性越大，應作為最優特徵

G a i n (D, a) = E n t (D) - \sum_{v = 1}^{v} \frac{D^{v}}{D} E n t (D^{v})

增益率：增益比率度量是用前面的增益度量Gain(S，A)和所分離資訊度量SplitInformation(如上例的性別，活躍度等)的比值來共同定義的。

公式如下：

G a i n R a t i o (S_{A}, A) = \frac{G a i n (S_{A}, A)}{S p l i t I n f o r m a t i o n (S_{A}, A)}

S p l i t I n f o r m a t i o n (S_{A}, A) = - \sum_{m \in M} \frac{| S_{A m} |}{| S_{A} |} l o g \frac{S_{A} m}{S_{A}}

例子：
如下圖，第一列為論壇號碼，第二列為性別，第三列為活躍度，最後一列使用者是否流失
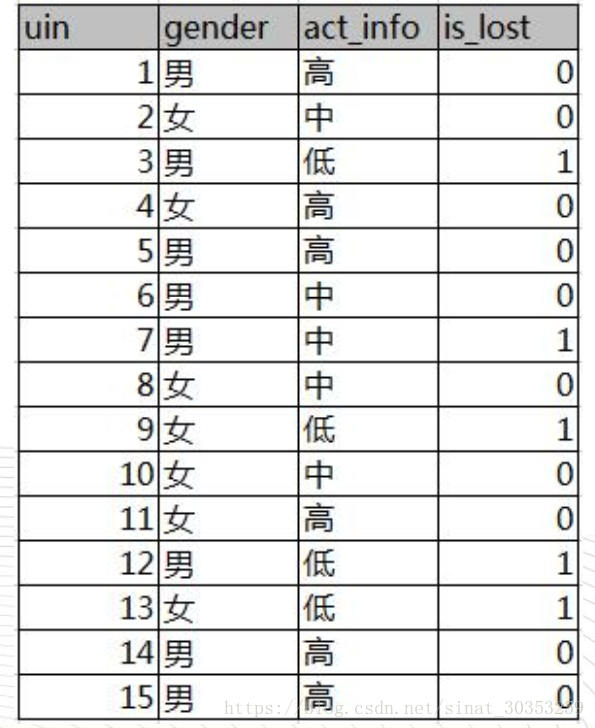
這裡寫圖片描述

其中Positive為正樣本（已流失）， Negative為負樣本
（未流失），下面的數值為不同劃分下對應的人數。可得到三個熵：
整體熵：

E (S) = - \frac{5}{15} l o g_{2} (\frac{5}{15}) - \frac{10}{15} l o g_{2} (\frac{10}{15}) = 0.9182

性別熵：

E (g_{1}) = - \frac{3}{8} l o g_{2} (\frac{3}{8}) - \frac{5}{8} l o g_{2} (\frac{5}{8}) = 0.9543

E (g_{2}) = - \frac{2}{7} l o g_{2} (\frac{2}{7}) - \frac{5}{7} l o g_{2} (\frac{5}{7}) = 0.8631

性別資訊增益：

I G a i n (S, g) = E (s) - \frac{8}{15} E (g_{1}) - \frac{7}{15} E (g_{2}) = 0.0064

機器學習之決策樹演算法詳解

1-1 基本流程

一、概念：

二、劃分依據：

①熵

②特徵選擇–資訊增益及增益率

機器學習之決策樹演算法詳解

機器學習之決策樹演算法（一）

機器學習之決策樹演算法（1）

機器學習之決策樹演算法python實現

機器學習之決策樹演算法

小白自學機器學習之一文讀懂決策樹演算法詳解

機器學習之決策樹機器學習之K-近鄰演算法

機器學習之決策樹 Decision Tree（三）scikit-learn演算法庫

機器學習之決策樹（Decision Tree）文字演算法的精確率

分類演算法之決策樹ID3詳解

機器學習之決策樹與隨機森林模型

機器學習之決策樹（二）

[三]機器學習之決策樹與隨機森林

機器學習_8.決策樹演算法

機器學習之決策樹

機器學習之決策樹----python實現

【機器學習】決策樹演算法（二）— 程式碼實現

系統學習機器學習之決策樹

機器學習之決策樹(ID3)

機器學習之決策樹（一）