二分搜尋樹的刪除節點操作
本節我們來討論一下對二叉搜尋樹的刪除節點操作。
首先,我們先來研究一下稍微簡單一點的問題,如何刪除二叉樹中的最小值和最大值。
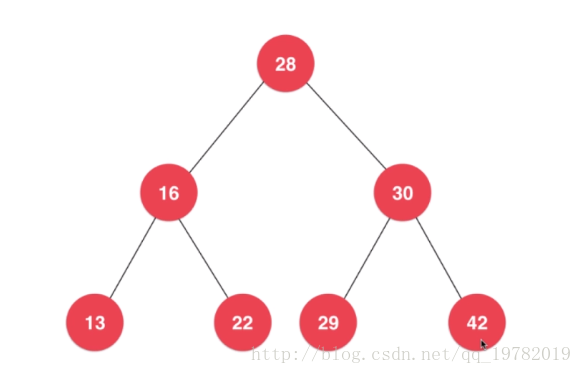
例如上圖的這一棵二叉樹中,最小值節點和最大值節點都在哪裡呢?我們可以很清楚的從圖中看出,13是該樹的最小節點,42是該樹的最大節點,且13節點位於樹的最左邊,而42位於樹的最右邊,這難道是一種巧合嗎?當然不是,首先,讓我們來回憶一下二叉樹的一個非常重要的性質。
二叉樹根節點的左子樹都比根節點小,右子樹都比根節點大。
也就是說,對於根節點28來說,他的左子樹都比28小,右子樹都比28大。那麼我們就看28的左子樹中的根16,而16又是一顆二叉樹的根節點,根據二叉樹根節點的左子樹都比根節點小,右子樹都比根節點大
先從簡單的問題開始,讓我們來先討論一下如何找到一顆二叉樹的最小節點吧。
通過上面的討論,我們已經瞭解到了一棵二叉樹的最小值節點位於這顆樹的“最左邊”,最大節點位於這棵樹的“最右邊”,因此我們可以很容易的寫出一個查詢二叉樹中最小節點的方法,程式碼如下所示:
// 返回以node為根的二分搜尋樹的最小鍵值所在的節點 node* minmum(node* node){ if( node->left == NULL )//如果該節點不存在左子樹了,那麼該節點就是這課樹的最小節點 return node; return minmum(node->left);//如果該節點還存在左子樹,說明該節點並不是最小節點
//則必須繼續往它的左子樹搜尋下去(運用遞迴的方法)
}二叉樹根節點的左子樹都比根節點小,右子樹都比根節點大。
二叉樹根節點的左子樹都比根節點小,右子樹都比根節點大。
二叉樹根節點的左子樹都比根節點小,右子樹都比根節點大。
重要的事情說三遍!!上面這句話概括了這個演算法的核心思想。
對於查詢一棵樹的最大節點,同理程式碼如下:
// 返回以node為根的二分搜尋樹的最大鍵值所在的節點
node* maximum(node* node){
if( node->right == NULL )//如果該節點沒有右子樹了,說明為最大的節點
return node;
return maximum(node->right);//該節點還存在右子樹的話,說明還有比它更大的節點存在 //因此該節點肯定不是最大節點,我們還要往“右邊”搜尋
}現在我們知道了如何查詢到一顆樹中的最小節點和最大節點了,那麼要刪除這個節點該怎麼做呢?
這個時候,我們就要分情況一個一個討論了。
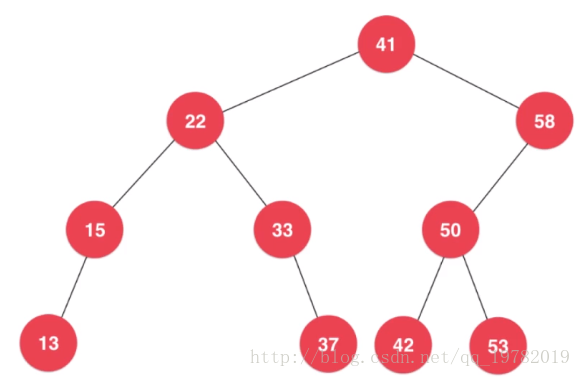
例如我們拿下面的這棵二叉樹來討論:
首先,我們可以很清楚的找到這棵二叉樹的最小節點是13節點,我們要刪除它直接delete掉這個節點就好了,接下來,15是最小節點,我們也delete掉,然而,對於接下來的最小節點22來說,這個節點貌似就不是這麼簡單的就能夠刪除了。
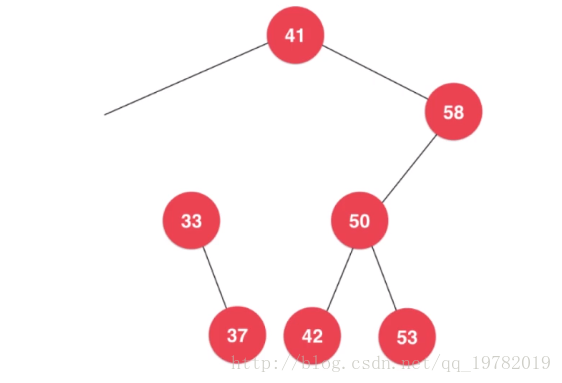
如果我們直接把22節點給delete掉,我們來看一下會發生什麼樣的問題。
雖然22節點成功刪除了,但是,22的右子樹卻也因為22節點的刪除而與原來的二叉樹給“斷開了”,那麼這是失敗的一次刪除,因為我們在刪除22節點的同時,還破壞了這棵樹的完整性。那麼,我們有什麼好的辦法呢?
辦法當然是有的,首先,雖然22節點被刪除了,但是22節點雖然沒有左子樹了,但是它的右子樹我們不能“丟棄”人家,我們要讓它重新與原來的樹給連線起來,那麼對於這段“被丟棄”的右子樹的樹根來說,我們想一想它具有什麼特點呢?33節點能完美的替代被刪除的22節點的位置嗎?能不能替代,在二叉樹中就是判斷這兩個節點在樹中的“狀態”是不是一樣的。對於被刪除的22節點來說,22節點比它的根節點41小,且小於它的左子樹,大於它的右子樹。而對於“被丟棄”的右子樹的樹根節點33來說,因為它也處於樹根節點41的的子樹中,也就是它比根節點41小,而且本來滿足它比它的左子樹小,右子樹大的特點,因此我們發現,33節點與被刪除的22節點此時代表的是完全的一樣的,因此我們只要把33節點的地址返回給上一層節點(41節點),作為其新的左孩子,這樣,我們不僅把22節點成功刪除了,而且也使得22節點的右子樹沒有被“拋棄”,並且重新和原來的樹組合起來,完美的符合了二叉樹的結構特點。那麼就讓我們來看一下具體的程式碼吧。
//刪除rootnode為根的二叉樹的最小值,並且把刪除後的樹的地址返回
node*removemin(node*rootnode){
if(rootnode->left==NULL){//遍歷到了樹中最左邊的節點,也就是該樹中最小的節點
node*rightroot=rootnode->right;//把要刪除的節點的右子樹根節點的地址儲存好
delete rootnode;//需要先記錄右子樹地址在刪除節點,否則先刪除節點則丟失了右子樹根節點的地址
count--;
return rightroot;//把右子樹的根地址返回到上一層以供連線使用
}
rootnode->left=removemin(rootnode->left);//連線記錄好的右子樹的根地址,重組為父節點的左子樹
return rootnode;
}其中的引數rootnode第一次代表的是需要本刪除最小節點的樹根地址,後面每次遞迴中的rootnode都為本層節點的地址。
同理,刪除樹中最大節點的程式碼如下:
// 刪除以rootnode為根的二叉樹的最大節點,並把新樹的根節點返回
node*removemax(node*rootnode){
if(rootnode->right==NULL){//遍歷到了樹中最大節點的位置
node*leftnode=rootnode->left;//儲存住被刪除節點左子樹的根節點地址
delete rootnode;//需要先記錄左子樹地址在刪除節點,否則先刪除節點則丟失了左子樹根節點的地址
count--;
return leftnode;//返回上一級做連線使用
}
rootnode->right=removemax(rootnode->right);//連線被脫離的子樹
return rootnode;//返回當前節點的地址
}好了,現在我們已經能夠很輕鬆實現刪除一棵以root為根的二叉樹的最小值和最大值,並且把新樹的根地址返回的方法了。那麼,讓我們現在來繼續往更深入的探討一下,如何刪除二叉樹中的任意一個節點呢?
讓我們想一想,在二叉樹中的每一棵節點,存在哪幾種狀態呢?
1.無左子樹,無右子樹。
2.無左子樹,有右子樹。
3.有左子樹,無右子樹。
4.既有左子樹,也有右子樹。
因此,我們在刪除樹中的一個節點來說,也要去分情況討論了。
1.無左子樹,無右子樹。
這種情況很簡單,我們只要刪除該節點,並且返回一個NULL值給上一層節點做連線使用(可能是被連線到上一層節點的左子樹也可能是右子樹),但是都不影響二叉樹的結構。
1.無左子樹,有右子樹。
此時這種情況就和我們刪除一棵樹中的最小節點的處理方法類似了。我們只需要先把被刪除節點的右子樹資訊(右子樹根地址)給儲存下來以備上一層連線使用,然後在去刪除該節點(順序不能反,否則先把節點刪除了,則也丟失了該節點右子樹的資訊,右子樹也一起消失了)。
3.有左子樹,無右子樹
此時這種情況就和我們刪除一棵樹中的最大節點的處理方法類似了。我們只需要先
把被刪除節點的左子樹資訊(左子樹根地址)給儲存下來以備上一層連線使用,然後在
去刪除該節點(順序不能反,否則先把節點刪除了,則也丟失了該節點左子樹的資訊,
左子樹也一起消失了)。
4.既有左子樹,也有右子樹。
這種情況是最複雜的,處理起來也是最難的。:
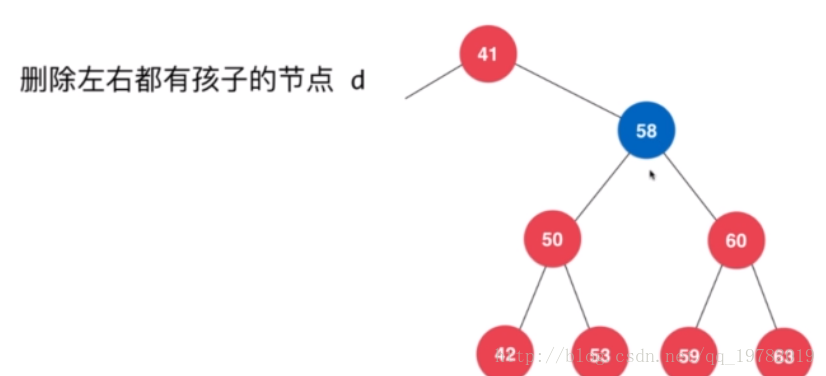
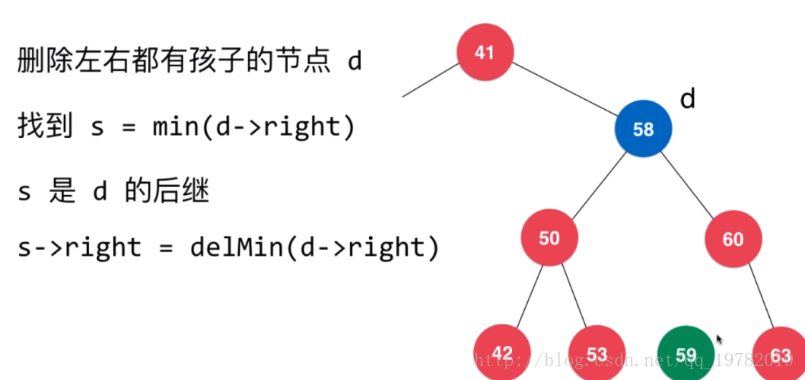
假設我們要刪除58這個節點,但是58既有左子樹,也有右子樹,那麼我們應該選擇哪一
個節點作為“替代節點呢”?上面我們討論了刪除只含有單邊子樹情況是如何挑選替代節點
就是其左子樹或右子樹的樹根作為替代節點(也就是該節點的左孩子或者右孩子)。然而,
此時我們這個節點既含有左子樹也還有右子樹,那麼該選哪個孩子作為節點呢?是50節點
還是56節點呢?答案是哪個孩子節點都不選。因為他們都不符合58節點所處的“狀態”。
那麼58節點此時的狀態是怎怎樣的呢?還是回到我們對於二叉樹結構的定義上:二叉
樹根節點的左子樹都比根節點小,右子樹都比根節點大。
我們發現,58節點比它左子樹所有的節點都要小,比它右子樹所有節點都要大。那麼,假設我們讓左孩子50替代58的位置,我們來看一看,50確實是比58的右子樹所有的節點都要小,但是50卻並不比58左子樹的所有節點都要大,比如其中的53節點就要比50大,因此50節點肯定是不符合二叉樹結構的特點的,也就不能去代替58節點的位置了。那麼我們再來看一下58的右孩子60能否替代58節點的位置呢?如果60替代58節點的位置,原來58節點的左子樹的所有節點確實比60要小,滿足左子樹的關係,但是58的右子樹的所有節點卻並不是都比60大,比如其中的59節點。因此58的右孩子60節點也不能夠完美的勝任這個任務。
那我我們應該選擇哪一個節點作為替代節點呢?我們發現,作為替代節點必須滿足的條件是:
二叉樹根節點的左子樹都比根節點小,右子樹都比根節點大。
因此,我們需要找58節點的替代節點,因為58節點的左子樹所有節點都比58小,所以如
果我們在58左子樹中找到一個最大的節點作為替代節點。則這個節點我們發現比58左子
樹的所有節點都要大,而且一定是比58節點的右子樹所有節點都要小的(因為該節點位
於58節點的左子樹,所以肯定比58節點的右子樹所有節點都要小,二叉樹的結構定義)。
此時,肯定有些聰明的同學會想到了,我們在58右子樹中找到一個最小節點作為替
代節點。這樣尋找替代節點也是可行的,一樣是符合二叉樹的結構定義的。右子樹的最
小節點本身就比右子樹所有節點要小,然後根據二叉樹的結構特點也能夠很輕鬆的得出
要比左子樹所有的節點都要大的。接下來我們以右子樹的最小節點作為替代節點來討論
我們現在已經知道了如何去尋找一個替代的節點的方法,就讓我們開始實踐一下具
體的程式碼吧:(該種情況我們取右子樹中的最小節點作為替代節點)
/*
* 刪除以node為根的二叉樹中的Key為key的節點
* 並且返回新二叉樹的根地址
*/
node* remove(node*Node,Key key){
if(Node==NULL){//如果樹為空的話
return NULL;//返回空值
}
else if(Node->key==key){//此時找到了需要被刪除的節點
if(Node->left==NULL){//待刪除節點的左子樹為空的話,右子樹為空或者不為空都不影響
node*rightnode=Node->right;//把右子樹的根地址儲存下來
delete Node;//節點此時可以被刪除了
count--;//更新計數器
return rightnode;//右子樹為空的話,返回NULL,不為空的話,返回右子樹的根節點
}
else if(Node->right==NULL){//此時待刪除節點的右子樹為空的話,左子樹為空或者不為空都不影響
node*leftnode=Node->left;//記錄左子樹的根地址,可能為空也可能為一個值,但不影響
delete Node;//此時可以刪除節點
count--;//更新計數器
return leftnode;//左子樹為空的話,返回NULL,不為空的話,返回左子樹的根節點
}
else{//此時待刪除節點的左右子樹均不為空的話
//替換節點可以是該節點右子樹中的最小值或者左子樹的最大值,這裡我們選右子樹中的最小值作為替換
node*replacenode=new node(minmum(Node->right)) ;//複製待刪除節點右子樹的最小節點作為替換節點
count++;//增加計數器
replacenode->right=removemin(Node->right);//刪除待刪節點的右子樹的最小值並把新樹的根地址再重新賦值給替代
//節點的右子樹
replacenode->left=Node->left;//替代節點的左子樹就是原來節點的左子樹
delete Node;//替代節點的左右子樹都已經更新完畢了,可以刪除了
count--;//更新計數器
return replacenode;//返回替代節點的地址即新樹的根節點地址給上一層連線用
}
}
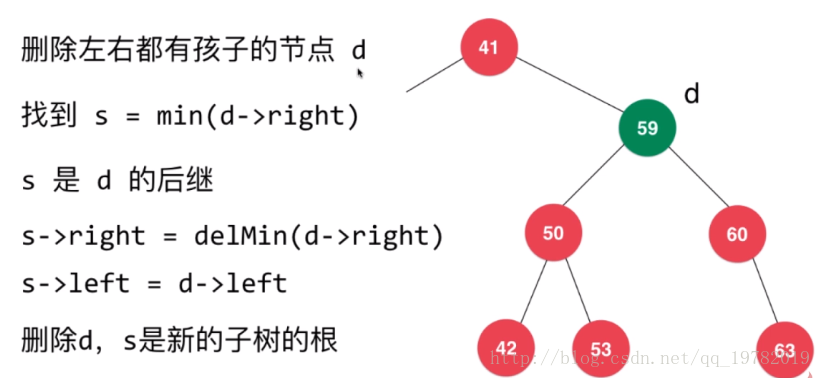
}我們找到了可以替代的節點為59節點,因此我們需要先複製一份59節點作為替代節點,
然後我們在用最開始寫的刪除樹中的最小值並返回新樹根地址的removemin()函式去
刪除右子樹中的最小值,然後在把新樹根的地址賦值給“複製節點”作為其新的右孩子,
而“複製節點”的左孩子就是將要被刪除的58節點原來的左孩子,我們只需要把58節點的
左子樹的根地址賦值給“複製節點”的左孩子就好了,此時“複製節點”就應經完成了應有
的連線操作,我們就可以放心的把58節點給直接刪除了,接著更新計數器,把“替代節點”
作為新樹的根節點返回給上一層去連線使用。
以下是測試函式:
int main()
{
BST<int,int> a=BST<int,int>();
a.insert(3,4);
a.insert(1,4);
a.insert(5,4);
a.insert(2,4);
a.leverorder();
a.removemin();
cout<<endl;
cout<<"delete the min:"<<endl;
a.leverorder();
cout<<endl;
a.removemax();
cout<<"delete the max:"<<endl;
a.leverorder();
cout<<endl<<"delete the 3"<<endl;
a.remove(3);
a.leverorder();
測試結果如下:
3 1 5 2
delete the min:
3 2 5
delete the max:
3 2
delete the 3
2
如果想要獲取二叉樹所有的完整程式碼,請點選此處進入GitHub程式碼倉庫。