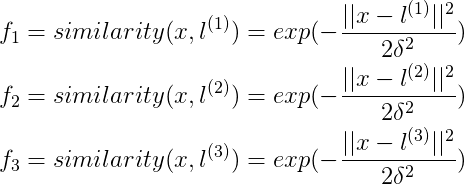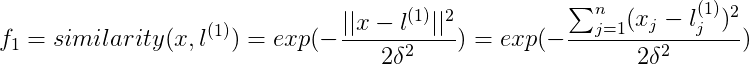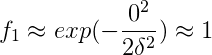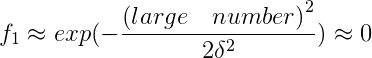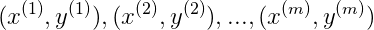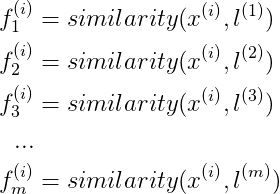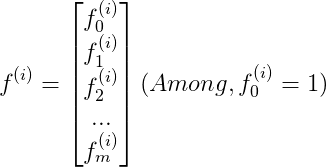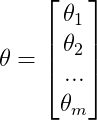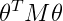Machine Learning第七講SVM --(二)核函式
阿新 • • 發佈:2018-12-27
一、Kernels I(核函式I)
在非線性函式中,假設函式為:

將表示式改變一下,將其寫為:
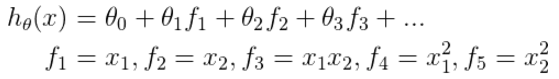
聯想到上次講到的計算機視覺的例子,因為需要很多畫素點,因此若f用這些高階函式表示,則計算量將會很大,那麼對於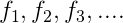
由此引入核函式的概念。
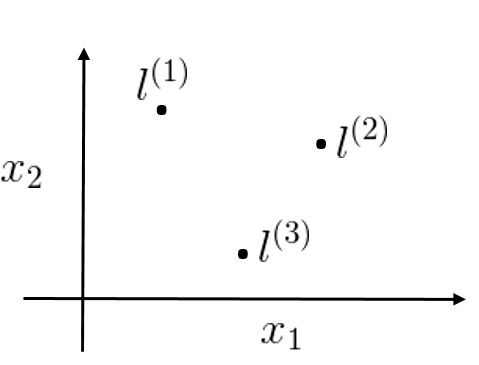
對於給定的x,
其中,similarity()函式叫做核函式(kernel function)又叫做高斯核函式,其實就是相似度函式,但是
我們平時寫成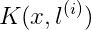
這裡將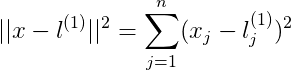
若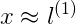
若x is far from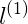
下面的圖形會給出比較直觀的感受:

在此基礎上,看下面的例子:

對於紫色的點x,因為其距離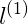
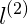
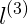
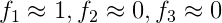
對於藍色的點,因為其距離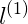
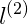
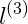

通過選取很多這樣的x值,得到他們的預測值,得到邊界,如圖紅色不規則封閉圖形所示,在圖形內部預測值為y=1,在圖形外部的預測值y=0。
二、Kernels II(核函式II)
上面Kernels I內容中講到了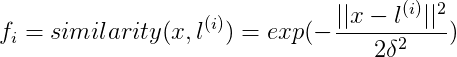

我們採取的方法是將每一個樣本都作為一個標記點。
SVM with Kernels
給出
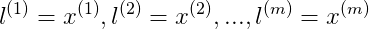 。
。
對於x,則有
有向量
其中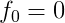
對於訓練樣本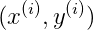
其中,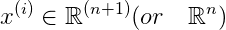
且
於是,假設函式變成
其中,m為訓練集的大小
帶核函式的代價函式為:
注意:這裡我們仍然不把θ0計算在內。
最小化這個函式,即可得到支援向量機的引數。
若涉及到一些優化問題,可以選擇n=m。
另外,說明:

另外,在實際應用中有人將其實現為下述公式,這是另一種略有區別的距離度量方法,這種方法可以適應超大的訓練集:
因為若使用第一種方法,當m非常大時,求解很多引數將會成本非常高。

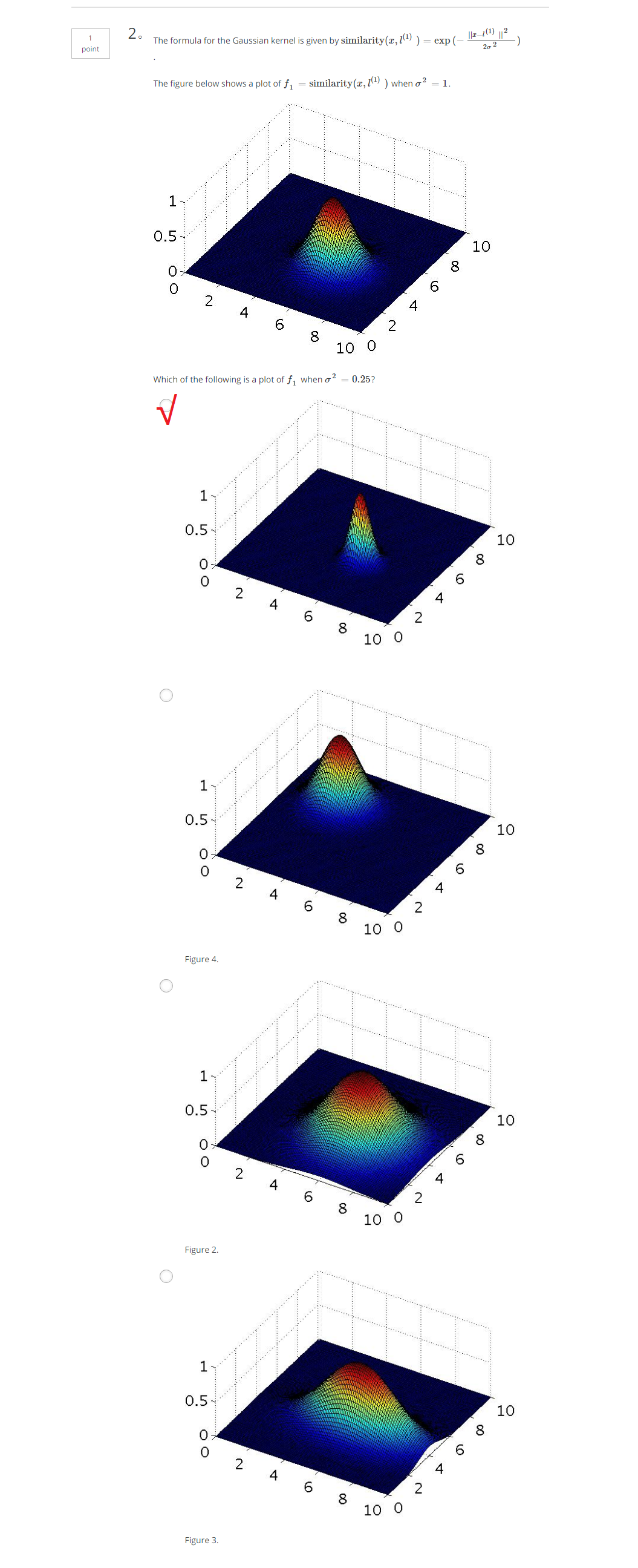
附上一題關於f_i引數的題目: