ROC曲線和AUC
本博文所有理論都是基於二分類,多分類問題其實與二分類問題想通。
- 1,首先區分什麼是正類什麼是負類。
考慮一個二分問題,如果一類定為正類(positive),那麼另一類就是負類(negative)。
注意和正樣本和負樣本概念不同,參考博文:https://blog.csdn.net/u010916338/article/details/84974188
- 2,對一個二分問題來說,會出現四種情況:真正類,假正類,真負類,假負類。
真正類(True positive):例項是正類並且也被 預測成正類;
假正類(False positive):例項是負類被預測成正類;
真負類(True negative):例項是負類被預測成負類;
假負類(false negative):例項是正類被預測成負類。


- 3,TPR和FPR
真正類率(true positive rate ,TPR), 計算公式為TPR=TP/ (TP+ FN),刻畫的是分類器所識別出的正例項佔所有正例項的比例。
假正類率(false positive rate, FPR),計算公式為FPR= FP / (FP + TN),計算的是分類器錯認為正類的負例項佔所有負例項的比例。1-specificity=FPR。
注意:兩者的分母不同。
- 4,ROC的引入
在一個二分類模型中,對於所得到的連續結果,假設已確定一個閾值,比如說 0.6,大於這個值的例項劃歸為正類,小於這個值則劃到負類中。如果減小閾值,減到0.5,固然能識別出更多的正類,也就是提高了識別出的正例佔所有正例的比例,即TPR,但同時也將更多的負例項當作了正例項,即提高了FPR。為了形象化這一變化,在此引入ROC。
Receiver Operating Characteristic,翻譯為"接受者操作特性曲線",夠拗口的。曲線由兩個變數1-specificity 和 Sensitivity繪製. 1-specificity=FPR橫軸表示,Sensitivity=TPR縱軸表示。這個組合以1-specificity對sensitivity,即是以代價(costs)對收益(benefits)。
- 5,舉例
現有兩種水果,橘子和橙子,共61800個。已知橙子有14084個設為正類,已知橘子有47716個設為負類。假設分類器為BP神經網路,且輸出層只有一個神經元,且神經元的輸出值為0~1之間的小數值。現設定閾值,比如0.6,但凡輸出層神經元的輸出值大於等於0.6都認為是橙子,小於0.6都認為是橘子。
現將所有輸出結果從大到小排序,每6180條資料做一次擷取,並做一次TPR和FPR統計。
解析:因為已經排了序,每移動6180個數據(即移動10%),其實就相當於移動了閾值。例如大於0.91的有10%,大於0.83的有20%。
統計結果如下表。例項數指每一組的資料總數,包含正類也包含負類。正例數指真正類數,注意表中的正例數是每一段6180資料中的真正類數,具體計算還需加上前面的統計資料。
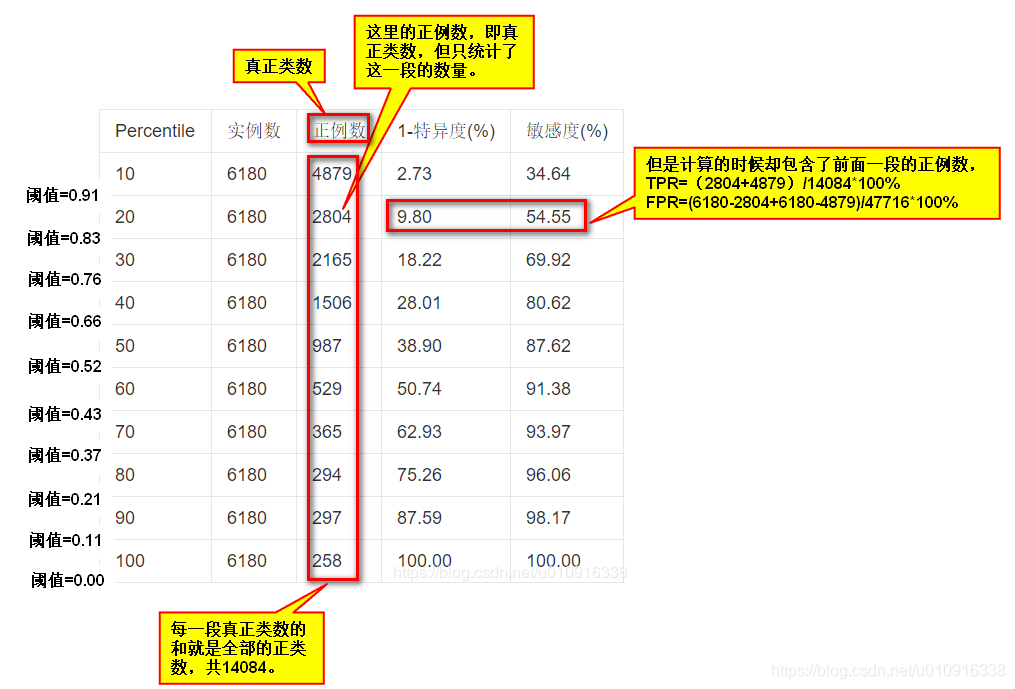
如下圖,可以換個思路去理解,即損失率對應收益率。比如從下往上第一個點,損失0%那麼就收益0%;第二個點損失2.73%那麼就會收益34.64%。

- 6,AUC
最好的狀態是,無論損失率為多少,收益率都最高,那麼該模型就是最好的。從上圖中反應出來就是橫軸無論取值為多少,縱軸都取值為100%。如下圖率線所示:
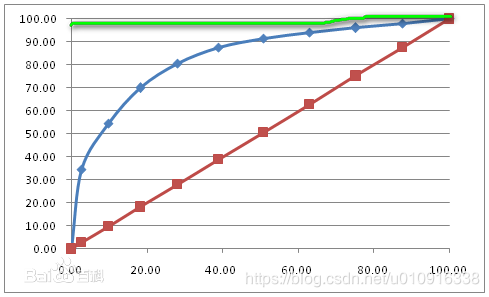
進一步發現,此時綠色曲線與橫軸座標圍成的面積最大,那麼就可以轉換成用ROC曲線與橫軸座標圍成的面積來表示模型的準確率,於是誕生了AUC。
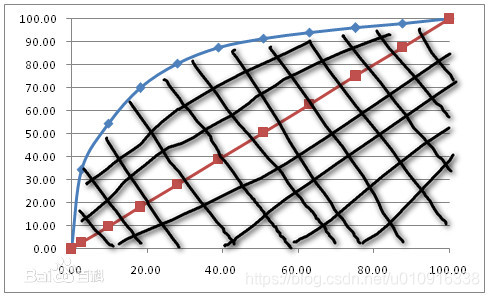
但是AUC也有缺陷
參考論文:The Relationship Between Precision-Recall and ROC Curves
