Table of Contents

Purpose

In the pursuit of the AGI (Artificial General Intelligence), we need to widen the domains in which our agents excel. Creating a program that solves a single game is no longer a challenge and it stands true even for the relatively complex games with enormous search spaces like Chess (

We have a prototype of this - the human brain. We can tie our shoelaces, we can ride cycles and we can do physics with the same architecture. So we know this is possible. Demis Hassabis - Deep Mind’s CEO

Let’s create an agent that learns by mimicking the human brain and generalizes enough to play multiple distinct games.

Introduction to Reinforcement Learning

Before we proceed with solving Atari games, I would recommend checking out my previous intro level article about Reinforcement Learning, where I have covered the basics of gym and DQN.

Data preparation

In the opposition to the above example of the cartpole project, where we’ve used game specific inputs (like cart position or pole angle), we are going to be more general in the Atari project…

… and use something that all Atari games have in common - pixels.

Let’s pause a game, look at the screen and find out what we can derive from it.

We can see the position of the paddle, we can see the ball and the blocks.

But do we have all the information to determine what’s really going on?

No, we don’t have any information about the movements of the game objects and I hope we all can agree that’s it crucial in the world of games.

How can we overcome this?

Let’s for each observation stack two consecutive frames.

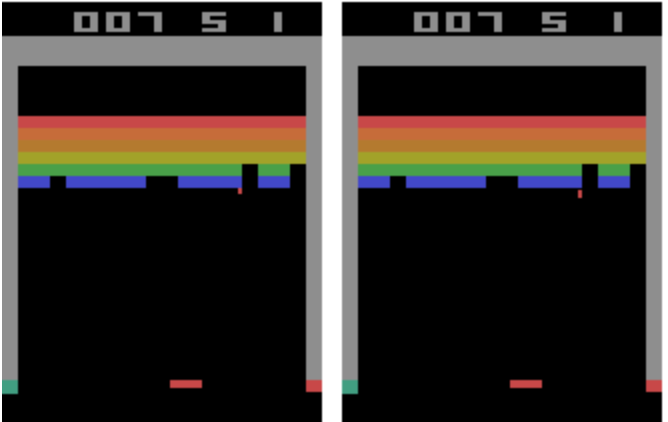
Okay, now we can see the direction and velocity of the ball.

But do we know it's acceleration?

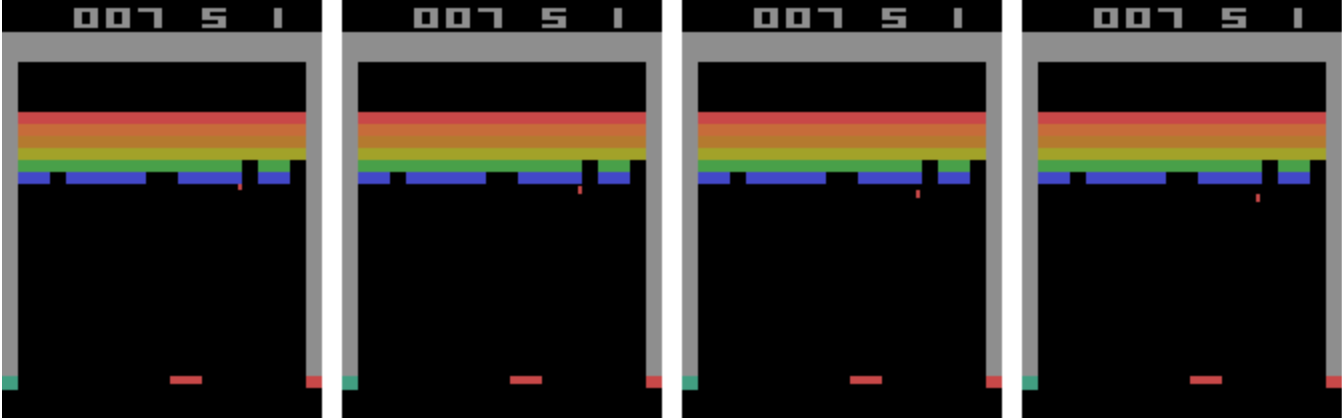
No. Let’s stack three frames then.

Now we can derive both the direction, velocity and acceleration of the moving objects, but as not every game is rendered at the same pace, we’ll keep 4 frames - just to be sure that we have all necessary information.

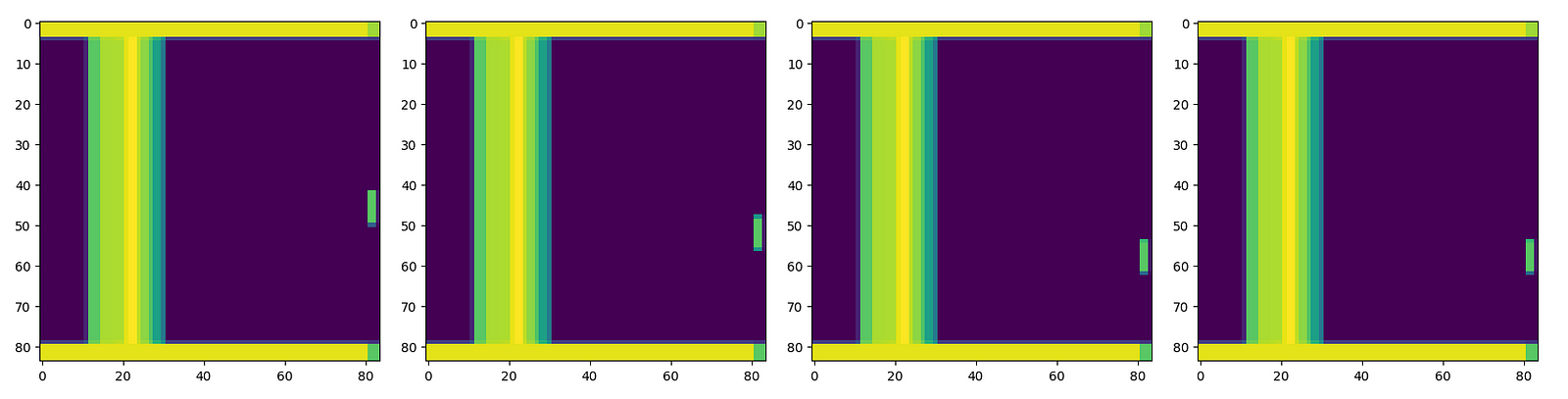
Having our observation defined by the last 4 frames, let’s focus on the image preprocessing. Atari environment outputs 210x160 RGB arrays (210x160x3).

That’s way too many pixels, definitely more than we need.

Firstly, let’s crop and downsample our images to 84x84 squares. We’ll use significantly less memory while still keeping all necessary information.

Then let’s convert the colors to the grayscale. We’ll reduce our observation vector from 84x84x3 to 84x84x1.

Assuming that for each observation we are going to store 4 last frames, our input shape will be 84x84x4.

Okay, technically we are ready to proceed.

But wait, can we do better? Yes!

Note that every single frame will be a part of 4 consecutive observations, so instead of copying it every time, we can use a reference to a single point in memory. We’ll significantly (by 4 times!) reduce our memory footprint and you’ll see how important it is while we proceed to the experience replay, where we are going to store up to a million of observations in RAM.

All of the above optimizations can be manually implemented, but instead of reinventing the wheel, feel free to use OpenAI’s wrappers that are tested and proved to be working.

Improvements to DQN

DDQN - Double Q-Learning

In my previous article (Cartpole - Introduction to Reinforcement Learning), I have mentioned that DQN algorithm by any means doesn’t guarantee convergence. While it was ‘enough’ to solve the cartpole problem, mostly due to the very limited discrete action space (Van Hasselt, Guez, & Silver, 2015), we may have to introduce various improvements for the more complex problems.

But why DQN might not converge?

Regular DQN tends to overestimate Q-values of potential actions in a given state. It wouldn’t cause any problems if all the actions were equally overestimated, but the case is, that once one specific action becomes overestimated, it’s more likely to be chosen in the next iteration making it very hard for the agent to explore the environment uniformly and find the right policy.

The trick to overcoming this is quite simple. We are going to decouple the action choice from the target Q-value generation. In order to do so we are going to have two separate networks, thus the name - Double Q-Learning. We will use our primary network to select an action and a target network to generate a Q-value for that action. In order to synchronize our networks, we are going to copy weights from the primary network to the target one every n (usually about 10k) training steps.

Formal notation:

Q-Target = r + γQ(s’,argmax(Q(s’,a,ϴ),ϴ’))

Code:

Experience Replay

Experience replay is a very important component of the Q-Learning and while its core wasn’t modified since the cartpole project, I have added two improvements that stabilizes and benefits the learning process:

1. Increased memory size - to 900k of entries, in order to remember both recent experiences, where the agent successfully exploits the environment and also the past ones, where the agent was focused mostly on the exploration.
2. Replay start size -each training starts with a uniformly random policy conducted for n (50k) number of steps. It populates the initial memory with completely random actions.

Convolutional Neural Network

Another major improvement was implementing the convolutional neural network designed by Deep Mind (Playing Atari with Deep Reinforcement Learning).

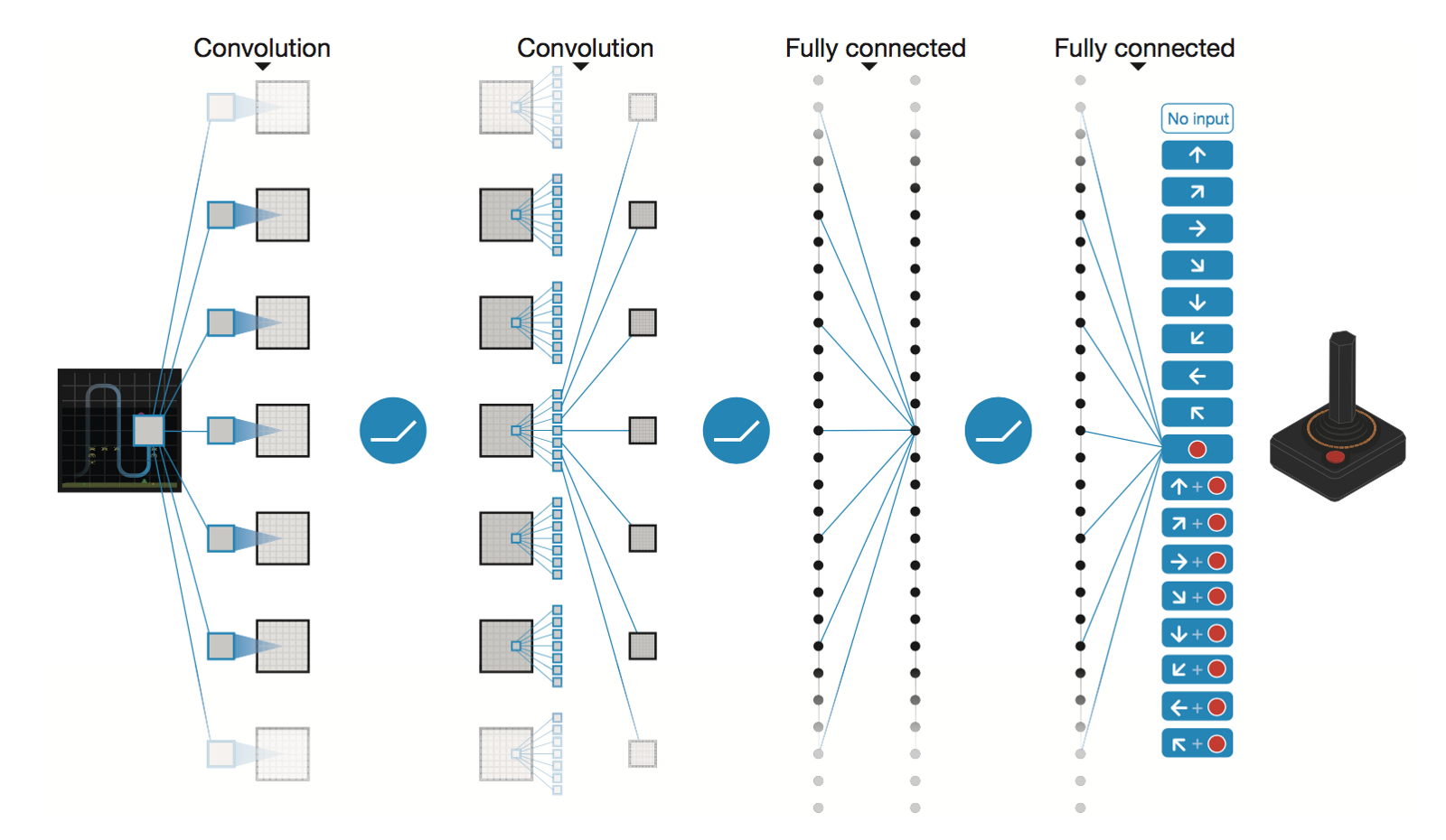
The input to the neural network consists of an 84 x 84 x 4 image produced by the preprocessing map, The first hidden layer convolves 32 filters of 8 x 8 with stride 4 with the input image and applies a rectifier nonlinearity. The second hidden layer convolves 64 filters of 4 x 4 with stride 2, again followed by a rectifier nonlinearity. This is followed by a third convolutional layer that convolves 64 filters of 3 x 3 with stride 1 followed by a rectifier. The final hidden layer is fully-connected and consists of 512 rectifier units. The output layer is a fully-connected linear layer with a single output for each valid action. The number of valid actions varied between 4 and 18 on the games we considered.

Code:

Performance

Both Breakout and SpaceInvaders were trained for 5M steps with the same hyperparameters presented below.

It usually takes about ~40h on Tesla K80 GPU or ~90h on 2.9 GHz Intel i7 Quad-Core CPU.

Note that training scores are normalized and each reward is clipped to (-1, 1).

Breakout