ROS tf的規則

$$T^{turtle1}_{turtle2} = T^{turtle1}_{world} * T^{world}_{turtle2}$$

• 其中，

  • 等號左邊：turtle2在turtle1座標系下的姿態。
  • 等號右邊第一項：turtle1在世界座標系world中的姿態的逆。
  • 等號右邊第二項：turtle2在世界座標系world中的姿態。

• 命令列中觀測座標變換資料的約定

$ rosrun tf tf_echo world turtle1
# 這將得到turtle1在世界座標系world中的姿態。

思考空間座標變換的方法：基底

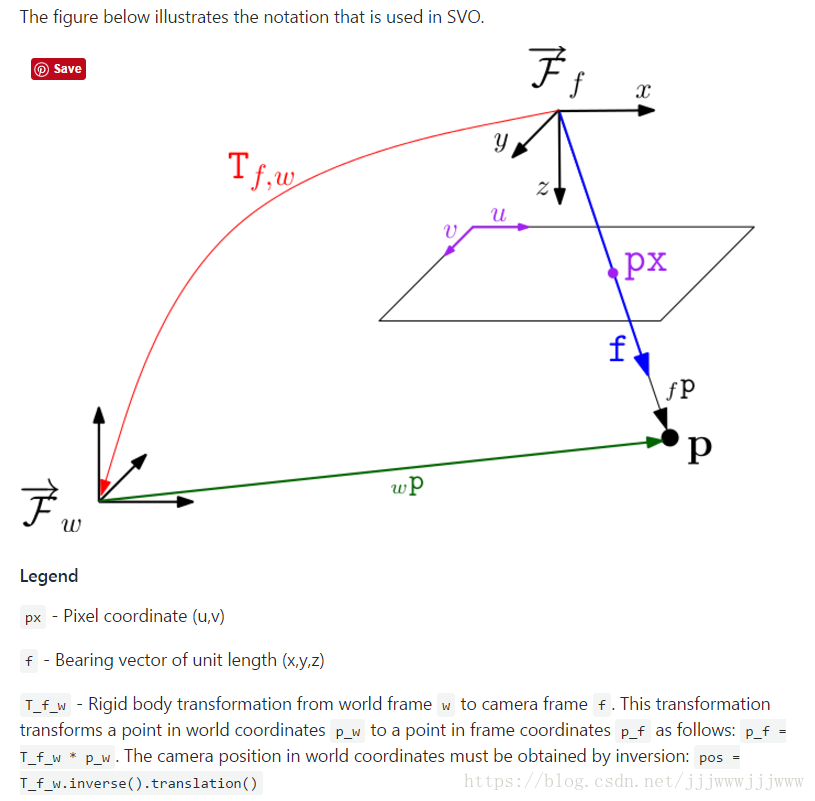
以下圖為例（影象來自SVO官網wiki）。

這裡，假定相機座標系$f$所在的向量空間的基底為$Base_f$，世界座標系$w$所在的向量空間的基底為$Base_w$。則座標變換的生成方式為：

$$T^f_w = Base_f^{-1} * Base_w$$
此時，若 $p_w$為空間某一點在世界座標系 $w$中的座標， $p_f$為該點在相機座標系 $f$中對應的座標，則有：
$$Base_w * p_w = Base_f * p_f$$
從而，
$$p_f = T^f_w * p_w$$
同理，
$$p_w = {T^f_w}^{-1} * p_f$$

則相機原點在世界座標系$w$中的座標值（即通常說的相機的位置）是：

$$p_w = {T^f_w}^{-1} * \mathbf{0} = T^w_f * \mathbf{0} = t^w_f$$
其中， $\mathbf{0}$是齊次座標 ${\begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}}^T$，其值為零表示相機座標系 $f$的座標原點，也即相機的位置， $p_f=\mathbf{0}$。
$t^w_f$是變換矩陣 $T^w_f$的平移部分。