網路模型複雜度計算方法
文章目錄
網路模型複雜度分析
Ml:
l層輸出 feature map 大小
Kl:
C: 通道數,其中
Cl−1為輸入通道數,
Cl為輸出通道數
時間複雜度
採用的單位一般使用浮點運算次數表示FLops(FLoating-point OPerations)
- 單層網路的時間複雜度
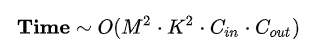
- 整個網路的時間複雜度
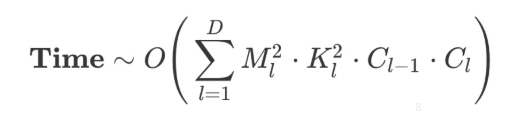
空間複雜度
包括兩部分
- 總引數量
- 各層輸出特徵圖。
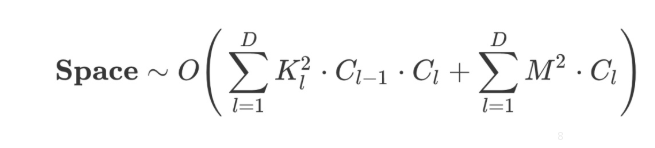
相關推薦
網路模型複雜度計算方法
文章目錄 網路模型複雜度分析 時間複雜度 空間複雜度 網路模型複雜度分析 M
演算法時間複雜度計算方法
一、概念: 時間複雜度是總運算次數表示式中受n的變化影響最大的那一項(不含係數) 比如:一般總運算次數表示式類似於這樣: a*2^n+b*n^3+c*n^2+d*n*lg(n)+e*n+f a ! =0時,時間複雜度就是O(2^n); a=0,b<
類似度計算方法
之間 ade length pri append 一個 lines 好的 javascrip 歐幾裏德距離 > 計算兩組數據之間的距離,偏好越類似的人其距離就越短。。。為了處理方便。須要一個函數來對偏好越相近的情況給出越大的值(0~1
演算法的時間複雜度和空間複雜度計算
一、演算法的時間複雜度定義 在進行演算法分析時,語句總的執行次數T(n)是關於問題規模n的函式,進而分析T(n)隨n的變化情況並確定T(n)的數量級。演算法的時間複雜度,也就是演算法的時間量度。記作:T(n)=O(f(
【Python例項第8講】模型複雜度影響
機器學習訓練營——機器學習愛好者的自由交流空間(qq 群號:696721295) 本講介紹模型複雜度怎樣影響預測精度和計算效能。我們使用的資料集仍然是波士頓房價資料集。對於模型的每一類,我們通過選擇有關的模型引數,度量計算效能和預測功效的影響,以此考察模型的複雜度。下面,我
圈複雜度計算例項
個人學習筆記, 網上摘抄. 計算公式1:V(G)=e-n+2p。其中, e表示控制流圖中邊的數量, n表示控制流圖中節點的數量, p圖的連線元件數目(圖的元件數是相連節點的最大集合)。因為控制流圖都是連通的,所以p為1. 計算公式2: V(G)=區域數=判定
評價頻繁模式挖掘和關聯分析的指標(模型興趣度度量方法)
強規則不一定是有趣的 關聯分析和頻繁模式挖掘的兩大經典演算法包括:Apriori演算法和FP-growth。 其在學習過程中的評價指標主要包括支援度(包括支援度計數)和置信度(也叫可信度)。但其實這兩個指標有一定的侷限性。 示例問題如下: 假設一共有10000個事務,其中包括A事件的
線性表——順序表——時間複雜度計算
資料結構的核心思想是通過資料結構的思維來優化程式碼的演算法,以此來提升程式的執行效能,縮短程式執行的時間。下面我來舉兩個例子,以此來說明資料結構的時間複雜度計算問題。 由於我這裡操作的是線性表——順序表,所以說先把線性表——順序表的原始碼貼出來 Ab
線性表——順序表——時間複雜度計算2
接上一篇文章繼續分析 在之前的文章中的示例1和示例2中,我們通過觀察可以發現,當在順序儲存結構的線性表中某個位置上插入或刪除一個數據元素時,其時間主要耗費在移動元素上(換句話說,移動元素的操作為預估演算法時間複雜度的基本操作),而移動元素的格式
pytorch學習: 構建網路模型的幾種方法
利用pytorch來構建網路模型有很多種方法,以下簡單列出其中的四種。 假設構建一個網路模型如下: 卷積層--》Relu層--》池化層--》全連線層--》Relu層--》全連線層 首先匯入幾種方法用到的包: import torch import torch.nn.functional as F
機器學習十二 誤差原因與模型複雜度
誤差原因(Error):用於測量模型效能的基本指標。 在模型預測中,模型可能出現的誤差來自兩個主要來源,即:因模型無法表示基本資料的複雜度而造成的偏差(bias),或者因模型對訓練它所用的有限資料過度敏感而造成的方差(variance)。 偏差:準確率和欠擬合 如果模型具
推薦系統中常見的幾種相似度計算方法和其適用資料
在推薦系統中,相似度的計算是一個很重要的課題。而相似度的計算方法多種多樣,今天我們來把這些方法比較一下,也為以後做專案留個筆記。其實無論是基於user的cf還是基於item的cf,亦或是基於svd的推薦,相似度計算都是必不可少的一步,只不過cf中計算相似度是一箇中間步驟,而
推薦演算法基礎--相似度計算方法彙總
推薦系統中相似度計算可以說是基礎中的基礎了,因為基本所有的推薦演算法都是在計算相似度,使用者相似度或者物品相似度,這裡羅列一下各種相似度計算方法和適用點 餘弦相似度 similarity=cos(θ)=A⋅B∥A∥∥B∥=∑i=1nAi×Bi∑i=1n(
資料結構-演算法-時間複雜度計算
演算法的時間複雜度定義為: 在進行演算法分析時,語句總的執行次數T(n)是關於問題規模n的函式,進而分析T(n)隨n的變化情況並確定T(n)的數量級。演算法的時間複雜度,也就是演算法的時間量度,記作:T(n}=0(f(n))。它表示隨問題規模n的增大,演算法執行時間的埔長率
資料結構與演算法-時間複雜度計算
一、方法 根本沒有必要計算時間頻度,即使計算處理還要忽略常量、低次軍和最高次剩的係數,所以可以採用如下簡單方法: 找出演算法中的基本語句:演算法中執行次數最多的那條語句就是基本語句,通常是最內層迴圈的迴圈體。 計算基本語句的執行次數的數量級:只需計算基本語句執行次數的數量級,這就
演算法複雜度的評估以及常用函式的複雜度計算
一、評估演算法複雜度 舉例: 演算法複雜度為O(n): 演算法複雜度為O(n2): 演算法複雜度為O(1+2+...+n) ---> O(n2): 演算法複雜度為O(lgN):
演算法之漢諾塔時間複雜度計算
設a, b, c是3個塔座:開始時,塔座a上有n個自上而下、由小到大地疊在一起圓盤,各圓盤從小到大編號為1, 2, …, n,現要求將塔座a上的這一疊圓盤移到塔座b上,並仍按同樣順序疊置,移動圓盤時遵守以下移動規則: 規則1:每次只能移動1個圓盤; 規則2:不允許將較大的圓
機器學習面試題之——簡單解釋正則化為什麼能減小模型複雜度
理論上,從VC維的角度可以解釋,正則化能直接減少模型複雜度。(公式理論略) 直觀上,對L1正則化來說,求導後,多了一項η * λ * sgn(w)/n,在w更新的過程中: 當w為正時,新的w減小,當w為負時,新的w增大,意味著新的w不斷向0靠近,即減小了模型複雜度。(
演算法的時間複雜度計算
時間複雜度與演算法步驟的多少是同樣的含義,計算演算法的總步驟就是時間複雜度。同時大O表示的是時間複雜度的上限。所以計算總步驟時可以按同數量級中最大情況來計算。 1.O(f(n)):輸入規模為n(n個數據)的演算法的時間複雜度為f(n)。 2.O(1):演算法的時間複雜度與輸
資料結構-時間複雜度計算詳解--向李紅老師的資料結構低頭 :)
今天早上突然想總結一下資料結構的時間複雜度的知識。 之前學了很多遍,但是一直沒有總結,所以之前參考了Algorithm還有清華大學出版的那個資料結構書,今天早上花了幾個小時好好的總結一下,也送給三班的同學們。 演算法的時間複雜度定義為: 在
