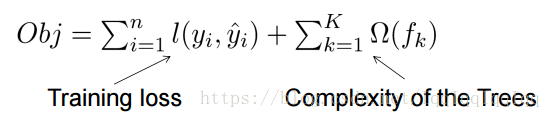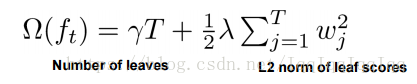本文轉自https://blog.csdn.net/IqqIqqIqqIqq/article/details/79820678

1對於xgboost，還有必要做很多特徵工程嗎？

特徵工程是個很廣的概念，包括特徵篩選、特徵變換、特徵合成、特徵提取等等。

對於xgboost，它能夠很好地做到特徵選擇，所以這一點不用我們去操心太多。

至於特徵變換（離散化、歸一化、標準化、取log等等），我們也不需要做太多，因為xgboost是基於決策樹，決策樹自然能夠解決這些。相比較來說，線性模型則需要做離散化或者取log處理。因為xgboost（樹類模型）不依賴於線性假設。但是對於分類特徵，xgboost需要對其進行獨熱編碼，否則無法訓練模型。

xgboost也可以免於一部分特徵合成的工作，比如線性迴歸中的互動項a:b，在樹類模型中都可以自動完成。但是對於加法a+b，減法a-b，除法a-b這類合成的特徵，則需要手動完成。

絕大部分模型都無法自動完成的一步就是特徵提取。很多nlp的問題或者圖象的問題，沒有現成的特徵，你需要自己去提取這些特徵，這些是我們需要人工完成的。

綜上來說，xgboost的確比線性模型要省去很多特徵工程的步驟。但是特徵工程依然是非常必要的。

2.什麼時候該用LASSO，什麼時候該用Ridge？

這兩個都是正則化的手段。LASSO是基於迴歸係數的一範數，Ridge是基於迴歸係數的二範數的平方。根據Hastie, Tibshirani, Friedman的經典教材，如果你的模型中有很多變數對模型都有些許影響，那麼用Ridge；如果你的模型中只有少量變數對模型很大影響，那麼用LASSO。

LASSO可以使得很多變數的係數為0（相當於降維），但是Ridge卻不能。

因為Ridge計算起來更快，所以當資料量特別大的時候，更傾向於用Ridge。

最萬能的方法是用LASSO和Ridge都試一試，比較兩者Cross Validation的結果。

如果有很多多重共線性的變數，ridge的效果比lasso好。

最後補充一下，你也可以嘗試一下兩者的混合-Elastic Net。

3.如何簡單理解正則化？

從模型複雜度來理解的話，正則化就是奧卡姆剃刀正則化是奧卡姆剃刀的具體實現，在保持預測能力相當時，降低模型複雜度。

4.L2-norm為什麼會讓模型變得更加簡單？

斯坦福的一個講義裡說，在特徵都被標準化處理的情況下，迴歸係數越大，模型的複雜度越大。所以特徵係數變成0，模型複雜度會下降；係數變小，當然也是複雜度下降。

5.兩個變數不相關但是也不獨立的例子？

假設X是個隨機變數服從標準正態分佈，另一個隨機變數Y滿足Y=X2，那麼它們的協方差

cov(X,Y)=E(XY)−E(X)E(Y)=E(X3)−E(X)E(X2)=0−0×E(X2)=0

協方差為0，說明X和Y不相關。但是顯然X和Y不獨立。

6.xgboost是怎麼做到regularization的？

xgboost的目標函式是損失函式+懲罰項。從下面的式子可以看出，樹越複雜，懲罰越重。

樹的複雜度定義如下：

葉節點的數量和葉節點的得分越高，樹就越複雜。

7.為什麼lightgbm比xgb快？

LightGBM採用了基於梯度的單邊取樣（GOSS）的方法。

在過濾資料樣例尋找分割值時，LightGBM 使用的是全新的技術：基於梯度的單邊取樣（GOSS）；而 XGBoost 則通過預分類演算法和直方圖演算法來確定最優分割。在 Adaboost 中，樣本權重是展示樣本重要性的很好的指標。但在梯度提升決策樹（GBDT）中，並沒有天然的樣本權重，因此 Adaboost 所使用的取樣方法在這裡就不能直接使用了，這時我們就需要基於梯度的取樣方法。

梯度表徵損失函式切線的傾斜程度，所以自然推理到，如果在某些意義上資料點的梯度非常大，那麼這些樣本對於求解最優分割點而言就非常重要，因為算其損失更高。

GOSS 保留所有的大梯度樣例，並在小梯度樣例上採取隨機抽樣。比如，假如有 50 萬行資料，其中 1 萬行資料的梯度較大，那麼我的演算法就會選擇（這 1 萬行梯度很大的資料+x% 從剩餘 49 萬行中隨機抽取的結果）。如果 x 取 10%，那麼最後選取的結果就是通過確定分割值得到的，從 50 萬行中抽取的 5.9 萬行。在這裡有一個基本假設：如果訓練集中的訓練樣例梯度很小，那麼演算法在這個訓練集上的訓練誤差就會很小，因為訓練已經完成了。為了使用相同的資料分佈，在計算資訊增益時，GOSS 在小梯度資料樣例上引入一個常數因子。因此，GOSS 在減少資料樣例數量與保持已學習決策樹的準確度之間取得了很好的平衡。上文部分轉載機器之心。原論文連結如下

8.xgboost怎麼調參？

以python裡XGBClassifier為例。首先，要確定哪些引數要調，以下是比較重要和常用的引數。

max_depth: 每棵樹的最大深度。太小會欠擬合，太大過擬合。正常值是3到10。

learning_rate: 學習率，也就是梯度下降法中的步長。太小的話，訓練速度太慢，而且容易陷入區域性最優點。通常是0.0001到0.1之間。

n_estimators: 樹的個數。並非越多越好，通常是50到1000之間。

colsample_bytree: 訓練每個樹時用的特徵的數量。1表示使用全部特徵，0.5表示使用一半的特徵。

subsample: 訓練每個樹時用的樣本的數量。與上述類似，1表示使用全部樣本，0.5表示使用一半的樣本。

reg_alpha: L1正則化的權重。用來防止過擬合。一般是0到1之間。

reg_lambda: L2正則化的權重。用來防止過擬合。一般是0到1之間。

min_child_weight: 每個子節點所需要的樣本的數量（加權的數量）。若把它設定為大於1的數值，可以起到剪枝的效果，防止過擬合。

以上只是作為參考，通常我們只對其中的少數幾個進行調參，模型就可以達到很好的效果。

下一步就是對這些引數進行優化，最常用的是Grid Search。比如說我們要優化max_depth 和learning_rate。max_depth的候選取值為[3, 4, 5, 6, 7]，learning_rate候選取值為[0.0001, 0.001, 0.01, 0.1]。那麼我們就需要嘗試這兩個引數所有的可能的組合（共5*4=20個不同的組合）。通過交叉驗證，我們可以得到每個組合的預測評價結果，最後從這20個組合中選擇最優的組合。

Grid Search的想法簡單易行，但是缺陷就是當我們需要對很多參量進行優化時，我們需要遍歷太多的組合，非常耗時。比如說我們有5個參量需要優化，每個參量又有5個候選值，那麼就一共有5*5*5*5*5=3125種不同的組合需要嘗試，非常耗時。

另外一個常用的方法Random Search就可以解決這個問題。Random Search是從所有的組合中隨機選出k種組合，進行交叉驗證，比較它們的表現，從中選出最佳的。雖然Random Search的結果不如Grid Search，但是Random Search通常以很小的代價獲得了與Grid Search相媲美的優化結果。所以實際調參中，特別是高維調參中，Random Search更為實用。