2. 程式人生 > >資料結構(16)--圖的儲存及實現

資料結構(16)--圖的儲存及實現

阿新 • • 發佈：2019-02-02

參考書籍：資料結構（C語言版）嚴蔚敏吳偉民編著清華大學出版社    

    圖狀結構是一種比樹形結構更復雜的非線性結構。在樹狀結構中，結點間具有分支層次關係，每一層上的結點只能和上一層中的至多一個結點相關，但可能和下一層的多個結點相關。而在圖狀結構中，任意兩個結點之間都可能相關，即結點之間的鄰接關係可以是任意的。

1.鄰接矩陣

1.1結構定義

    圖和樹一樣，沒有順序映像的儲存結構，但可以藉助陣列的資料型別表示元素之間的關係。所以鄰接矩陣是用於描述圖中頂點之間關係(即弧或邊的權)的矩陣。   假設圖中頂點數為n，則鄰接矩陣An×n：

                1    若Vi和Vj之間有弧或邊
    A[i][j]=
                0    反之
    
    網的鄰接矩陣An×n：
                w （權值

）          若Vi和Vj之間有弧或邊
    A[i][j]=
                無窮大                   反之

注意：
1) 圖中無鄰接到自身的弧，因此鄰接矩陣主對角線為全零。
2) 無向圖的鄰接矩陣必然是對稱矩陣。
3) 無向圖中，頂點的度是鄰接矩陣對應行（或列）的非零元素之和；有向圖中，對應行的非零元素之和是該頂點的出度；對應列的非零元素之和是該頂點的入度；則該頂點的度是對應行和對應列的非零元素之和。

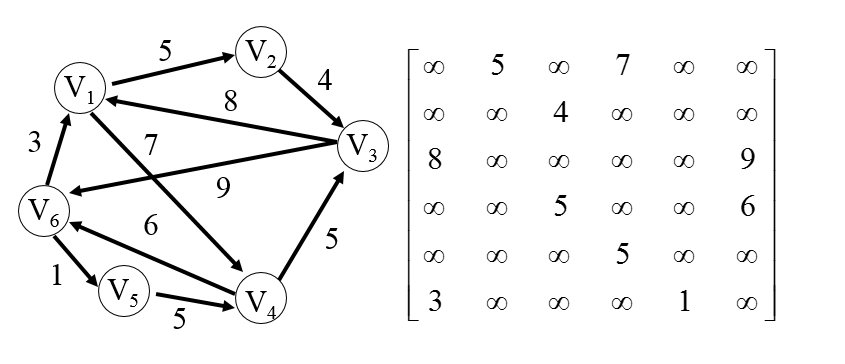
1.2示例

以有向網示例：


1.3程式碼實現

#include<stdio.h>
//#include<stdlib.h>
/*
圖的表示方法
DG（有向圖）或者DN（有向網）：鄰接矩陣、鄰接表（逆鄰接表--為求入度）、十字連結串列
UDG（無向圖）或者UDN（無向網）：鄰接矩陣、鄰接表、鄰接多重表
*/

//1.陣列表示法（鄰接矩陣）：將以有向網為例
#define INFINITY 32767//最大值：假定為無窮大
#define MAX_VERTEX_NUM 10//最大頂點數目
//typedef enum GraphKind {DG, DN, UDG, UDN};  //有向圖：0，有向網：1，無向圖：2，無向網：3

typedef int VRType;//頂點關係型別，對於無權圖或網，用0或1表示相鄰否；對於帶權圖或網，則為相應權值
typedef int VertexType;//頂點型別
typedef VRType AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct{
	VertexType vexs[MAX_VERTEX_NUM];//頂點向量
	AdjMatrix arcs;//鄰接矩陣
	int vexnum, arcnum;//圖的當前頂點數和弧數
	//GraphKind kind;//圖的種類標誌
}MGraph;//鄰接矩陣表示的圖
 
//若圖G中存在頂點v，則返回v在圖中的位置資訊，否則返回其他資訊
int locateVex(MGraph G, VertexType v){
	for(int i = 0; i < G.vexnum; i++){
		if(G.vexs[i] == v)
			return i;
	}
	return -1;//圖中沒有該頂點
}
//採用鄰接矩陣表示法構造有向網G
void createDN(MGraph &G){
	printf("輸入頂點數和弧數如:(5,3):");
	scanf("%d,%d", &G.vexnum, &G.arcnum);

	//構造頂點向量
	printf("輸入%d個頂點（以空格隔開如：v1 v2 v3）:", G.vexnum);
	getchar();//吃掉換行符
	for(int m = 0; m < G.vexnum; m++){
		scanf("v%d", &G.vexs[m]);
		getchar();//吃掉空格符
	}

	
	//初始化鄰接矩陣
	int i=0, j=0;
	for(i = 0; i < G.vexnum; i++){
		for(j = 0; j < G.vexnum; j++)
			G.arcs[i][j] = INFINITY;
	}

	//構造鄰接矩陣
	VertexType v1, v2;//分別是一條弧的弧尾和弧頭（起點和終點）
	VRType w;//對於無權圖或網，用0或1表示相鄰否；對於帶權圖或網，則為相應權值	
	printf("\n每行輸入一條弧依附的頂點（先弧尾後弧頭）和權值（如：v1 v2 3）:\n");
	fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
	for(int k = 0; k < G.arcnum; k++){
		scanf("v%d v%d %d",&v1, &v2, &w);
		fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
		i = locateVex(G, v1);
		j = locateVex(G, v2);
		G.arcs[i][j] = w;
	}
}
 
//列印鄰接矩陣
void printDN(MGraph G){
	printf("\n列印有向網G的鄰接矩陣：\n");
	for(int i = 0; i < G.vexnum; i++){
		for(int j = 0; j < G.vexnum; j++)
		{
			if(G.arcs[i][j] != INFINITY)
				printf("%9d ", G.arcs[i][j]);
			else
				printf("INFINITY  ");
		}
		printf("\n");
	}
	printf("\n");
}

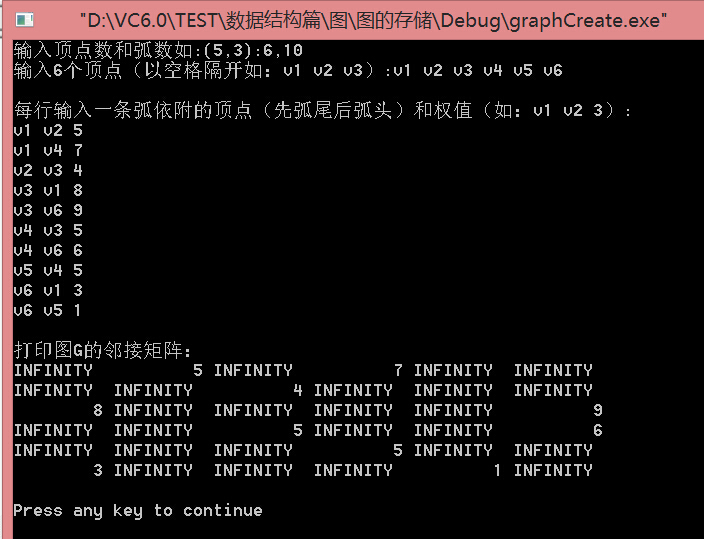
1.4演示

/*測試：
6,10
v1 v2 v3 v4 v5 v6

v1,v2,5
v1,v4,7

v2,v3,4

v3,v1,8
v3,v6,9

v4,v3,5
v4,v6,6

v5,v4,5

v6,v1,3
v6,v5,1
*/
void main(){
	MGraph G;
	createDN(G);	
	printDN(G);
}


2.鄰接表

2.1結構定義

類似樹的孩子連結串列。即對圖中的每個頂點vi建立一個單鏈表，表中結點表示依附於該頂點vi的邊或弧。           

          弧結點                                                                                         頂點結點（弧連結串列表頭結點）

                                                       

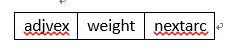
注意：
在無向圖的鄰接表中，
1）第i個連結串列中結點數目為頂點i的度；
2）所有連結串列中結點數目的一半為圖中邊數；
3）佔用的儲存單元數目為n+2e。
在有向圖的鄰接表中，
1）第i個連結串列中結點數目為頂點i的出度；
2）所有連結串列中結點數目為圖中弧數；
3）佔用的儲存單元數目為n+e。

為求出每一個頂點的入度，必須另外建立有向圖的逆鄰接表。有向圖的逆鄰接表與鄰接表類似，只是它是從入度考慮結點，而不是從出度考慮結點。

2.2示例

以無向網示例：

          

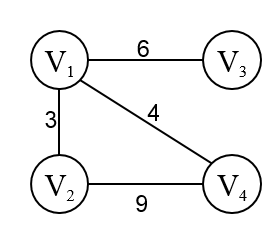
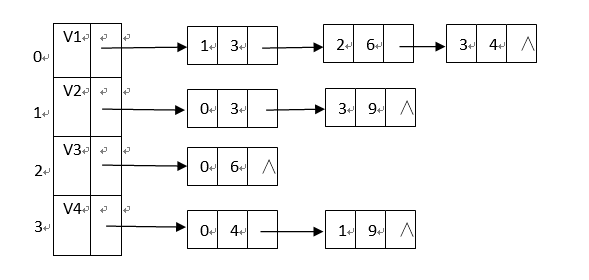
2.3程式碼實現

#include<stdio.h>
#include<stdlib.h>
/*
圖的表示方法
DG（有向圖）或者DN（有向網）：鄰接矩陣、鄰接表（逆鄰接表--為求入度）、十字連結串列
UDG（無向圖）或者UDN（無向網）：鄰接矩陣、鄰接表、鄰接多重表
*/
#define MAX_VERTEX_NUM 10//最大頂點數目
#define NULL 0
typedef int VRType;//對於帶權圖或網，則為相應權值
typedef int VertexType;//頂點型別
//typedef enum GraphKind {DG, DN, UDG, UDN};  //有向圖：0，有向網：1，無向圖：2，無向

typedef struct ArcNode{	
	int adjvex;//該弧所指向的頂點的在圖中位置
	VRType w;//弧的相應權值
	struct ArcNode *nextarc;//指向下一條弧的指標
}ArcNode;//弧結點資訊

typedef struct VNode{
	VertexType data;//頂點資訊
	ArcNode *firstarc;//指向第一條依附該頂點的弧的指標
}VNode, AdjVexList[MAX_VERTEX_NUM];//頂點結點資訊

typedef struct{
	AdjVexList vexs;//頂點向量
	int vexnum, arcnum;//圖的當前頂點數和弧數
	//GraphKind kind;//圖的種類標誌
}ALGraph;//鄰接表表示的圖
//若圖G中存在頂點v，則返回v在圖中的位置資訊，否則返回其他資訊
int locateVex(ALGraph G, VertexType v){
	for(int i = 0; i < G.vexnum; i++){
		if(G.vexs[i].data == v)
			return i;
	}
	return -1;//圖中沒有該頂點
}
//採用鄰接表表示法構造無向網G
void createUDN(ALGraph &G){
	printf("輸入頂點數和弧數如:(5,3):");
	scanf("%d,%d", &G.vexnum, &G.arcnum);

	//構造頂點向量,並初始化
	printf("輸入%d個頂點（以空格隔開如：v1 v2 v3）:", G.vexnum);
	getchar();//吃掉換行符
	for(int m = 0; m < G.vexnum; m++){
		scanf("v%d", &G.vexs[m].data);
		G.vexs[m].firstarc = NULL;//初始化為空指標////////////////重要！！！
		getchar();//吃掉空格符
	}

	//構造鄰接表
	VertexType v1, v2;//分別是一條弧的弧尾和弧頭（起點和終點）
	VRType w;//對於無權圖或網，用0或1表示相鄰否；對於帶權圖或網，則為相應權值	
	printf("\n每行輸入一條弧依附的頂點（先弧尾後弧頭）和權值（如：v1 v2 3）:\n");
	fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
	int i = 0, j = 0;
	for(int k = 0; k < G.arcnum; k++){
		scanf("v%d v%d %d",&v1, &v2, &w);
		fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
		i = locateVex(G, v1);//弧起點
		j = locateVex(G, v2);//弧終點
		
		//採用“頭插法”在各個頂點的弧鏈頭部插入弧結點
		ArcNode *p1 = (ArcNode *)malloc(sizeof(ArcNode));//構造一個弧結點，作為弧vivj的弧頭（終點）
		p1->adjvex = j;
		p1->w = w;
		p1->nextarc = G.vexs[i].firstarc;
		G.vexs[i].firstarc = p1;
		ArcNode *p2 = (ArcNode *)malloc(sizeof(ArcNode));//構造一個弧結點，作為弧vivj的弧尾（起點）
		p2->adjvex = i;
		p2->w = w;
		p2->nextarc = G.vexs[j].firstarc;
		G.vexs[j].firstarc = p2;
	}
}
//列印鄰接表
void printAdjList(ALGraph G){
	printf("\n");
	for(int i = 0; i < G.vexnum; i++){
		printf("依附頂點v%d的弧為：", G.vexs[i].data);
		ArcNode *p = G.vexs[i].firstarc;
		while(p){
			printf("v%dv%d(weight:%d) ", G.vexs[i].data, G.vexs[p->adjvex].data, p->w);
			p = p->nextarc;
		}
		printf("\n");
	}
	printf("\n");
}

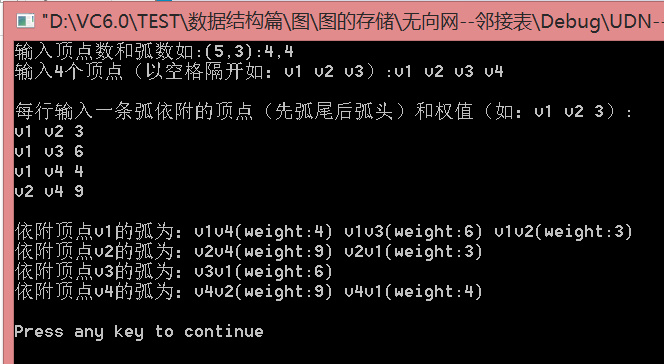
2.4演示

/*測試：
4,4
v1 v2 v3 v4

v1 v2 3
v1 v3 6
v1 v4 4
v2 v4 9
*/
void main(){
	ALGraph G;
	createUDN(G);
	printAdjList(G);
}


3.鄰接多重表

3.1結構定義

    在無向圖的鄰接表中，每條邊（Vi，Vj）由兩個結點表示，一個結點在第 i 個連結串列中，另一個結點在第 j 個連結串列中，當需要對邊進行操作時，就需找到表示同一條邊的兩個結點，這給操作帶來不便，在這種情況下采用鄰接多重表較方便。
    鄰接多重表中結點分為：邊結點和頂點結點 ：         

           弧結點                                                                                         頂點結點（弧連結串列表頭結點）

                         

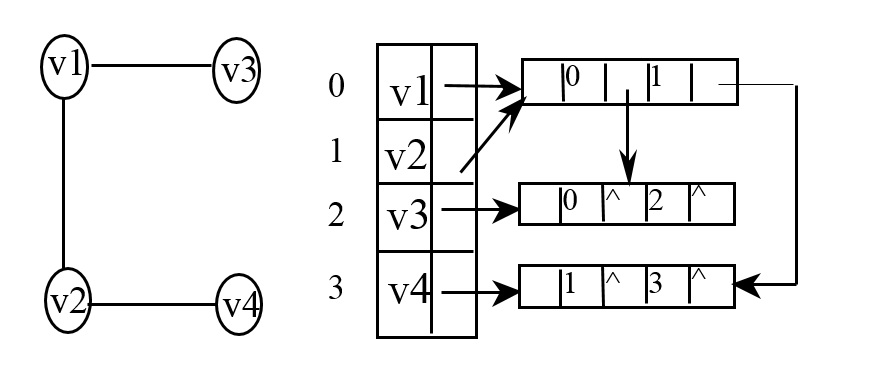
3.2示例

以無向圖示例：


3.3程式碼實現

#include<stdio.h>
#include<stdlib.h>
/*
圖的表示方法
DG（有向圖）或者DN（有向網）：鄰接矩陣、鄰接表（逆鄰接表--為求入度）、十字連結串列
UDG（無向圖）或者UDN（無向網）：鄰接矩陣、鄰接表、鄰接多重表
*/
#define MAX_VERTEX_NUM 10//最大頂點數目
#define NULL 0
//typedef int VRType;//對於帶權圖或網，則為相應權值
typedef int VertexType;//頂點型別
//typedef enum GraphKind {DG, DN, UDG, UDN};  //有向圖：0，有向網：1，無向圖：2，無向

typedef struct ArcNode{	
	int ivex, jvex;//該邊所依附的2個頂點的在圖中位置
	struct ArcNode *ivexNextarc, *jvexNextarc;//分別指向該邊所依附的兩個頂點下一條邊
}ArcNode;//弧結點資訊

typedef struct VNode{
	VertexType data;//頂點資訊
	ArcNode *firstedge;//指向第一條依附該頂點的弧的指標
}VNode, AdjMuitiVexList[MAX_VERTEX_NUM];//頂點結點資訊

typedef struct{
	AdjMuitiVexList vexs;//頂點向量
	int vexnum, arcnum;//圖的當前頂點數和弧數
	//GraphKind kind;//圖的種類標誌
}AMLGraph;//鄰接表表示的圖
//若圖G中存在頂點v，則返回v在圖中的位置資訊，否則返回其他資訊
int locateVex(AMLGraph G, VertexType v){
	for(int i = 0; i < G.vexnum; i++){
		if(G.vexs[i].data == v)
			return i;
	}
	return -1;//圖中沒有該頂點
}
//採用鄰接多重表表示法構造無向圖G
void createUDG(AMLGraph &G){
	printf("輸入頂點數和弧數如:(5,3):");
	scanf("%d,%d", &G.vexnum, &G.arcnum);

	//構造頂點向量,並初始化
	printf("輸入%d個頂點（以空格隔開如：v1 v2 v3）:", G.vexnum);
	getchar();//吃掉換行符
	for(int m = 0; m < G.vexnum; m++){
		scanf("v%d", &G.vexs[m].data);
		G.vexs[m].firstedge = NULL;//初始化為空指標////////////////重要！！！
		getchar();//吃掉空格符
	}

	//構造鄰接多重表
	VertexType v1, v2;//分別是一條的兩個頂點
	printf("\n每行輸入一條邊依附的頂點（如：v1v2）:\n");
	fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
	int i = 0, j = 0;
	for(int k = 0; k < G.arcnum; k++){
		scanf("v%dv%d",&v1, &v2);
		fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
		i = locateVex(G, v1);//邊依附的兩個頂點的在圖中的位置
		j = locateVex(G, v2);
		
		//採用“頭插法”在各個頂點的邊鏈頭部插入邊結點
		ArcNode *p = (ArcNode *)malloc(sizeof(ArcNode));//構造一個邊結點，它依附於vivj兩個頂點
		p->ivex = i;
		p->ivexNextarc = G.vexs[i].firstedge;
		G.vexs[i].firstedge = p;
		p->jvex = j;
		p->jvexNextarc = G.vexs[j].firstedge;
		G.vexs[j].firstedge = p;
	}
}
//列印鄰接多重表
void printAdjMultiList(AMLGraph G){
	printf("\n");
	for(int i = 0; i < G.vexnum; i++){
		printf("依附頂點v%d的邊為：", G.vexs[i].data);
		ArcNode *p = G.vexs[i].firstedge;

		while(p){
			if(p->ivex == i){
				printf("v%dv%d ", G.vexs[i].data, G.vexs[p->jvex].data);
				p = p->ivexNextarc;
			}else if(p->jvex == i){
				printf("v%dv%d ", G.vexs[i].data, G.vexs[p->ivex].data);
				p = p->jvexNextarc;
			}
		}
		printf("\n");
	}
	printf("\n");
}

3.4演示

/*
測試：
4,3
v1 v2 v3 v4

  v1v2
  v1v3
  v2v4
*/
void main(){
	AMLGraph G;
	createUDG(G);
	printAdjMultiList(G);
}


4.十字連結串列

4.1結構定義

十字連結串列是有向圖的另一種鏈式儲存結構。可以理解成有向圖的鄰接表和逆鄰接表的結合，在十字連結串列中，有兩種結點結構：         

             弧結點                                                                                      頂點結點（弧連結串列表頭結點）

          

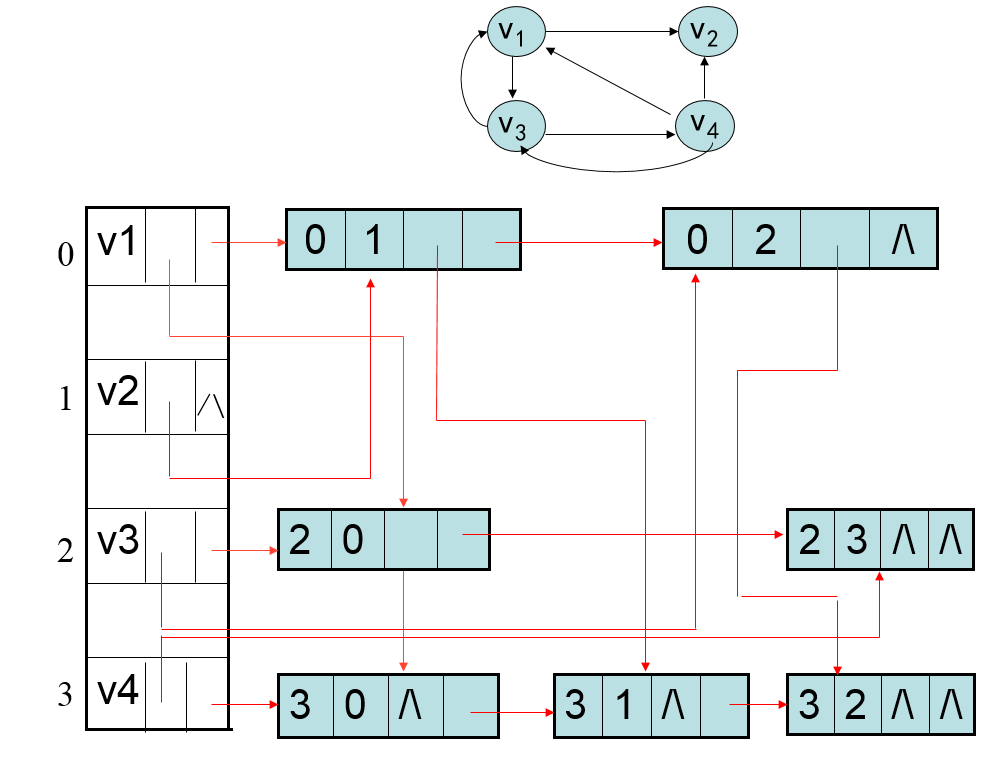
4.2示例

以有向圖示例：


4.3程式碼實現

#include<stdio.h>
#include<stdlib.h>
/*
圖的表示方法
DG（有向圖）或者DN（有向網）：鄰接矩陣、鄰接表（逆鄰接表--為求入度）、十字連結串列
UDG（無向圖）或者UDN（無向網）：鄰接矩陣、鄰接表、鄰接多重表
*/
#define MAX_VERTEX_NUM 10//最大頂點數目
#define NULL 0
//typedef int VRType;//對於帶權圖或網，則為相應權值
typedef int VertexType;//頂點型別
//typedef enum GraphKind {DG, DN, UDG, UDN};  //有向圖：0，有向網：1，無向圖：2，無向

typedef struct ArcNode{	
	int tailvex, headvex;//該弧的弧尾（起點）和弧頭（終點）所指向的頂點的在圖中位置
	struct ArcNode *tailNextarc, *headNextArc;//分別為指向弧尾（起點）相同的弧的下一條弧的指標、弧頭（終點）相同的弧的下一條弧的指標
}ArcNode;//弧結點資訊

typedef struct VNode{
	VertexType data;//頂點資訊
	ArcNode *firstIn;//指向第一條以該頂點為弧尾（起點）的指標
	ArcNode *firstOut;//指向第一條以該頂點的弧頭（終點）的指標
}VNode, VexList[MAX_VERTEX_NUM];//頂點結點資訊

typedef struct{
	VexList vexs;//頂點向量
	int vexnum, arcnum;//圖的當前頂點數和弧數
	//GraphKind kind;//圖的種類標誌
}OLGraph;//鄰接表表示的圖
//若圖G中存在頂點v，則返回v在圖中的位置資訊，否則返回其他資訊
int locateVex(OLGraph G, VertexType v){
	for(int i = 0; i < G.vexnum; i++){
		if(G.vexs[i].data == v)
			return i;
	}
	return -1;//圖中沒有該頂點
}
//採用十字連結串列表示法構造有向圖G
void createDG(OLGraph &G){
	printf("輸入頂點數和弧數如:(5,3):");
	scanf("%d,%d", &G.vexnum, &G.arcnum);

	//構造頂點向量,並初始化
	printf("輸入%d個頂點（以空格隔開如：v1 v2 v3）:", G.vexnum);
	getchar();//吃掉換行符
	for(int m = 0; m < G.vexnum; m++){
		scanf("v%d", &G.vexs[m].data);
		G.vexs[m].firstIn = NULL;//初始化為空指標////////////////重要！！！
		G.vexs[m].firstOut = NULL;
		getchar();//吃掉空格符
	}

	//構造十字連結串列
	VertexType v1, v2;//分別是一條弧的弧尾和弧頭（起點和終點）
	printf("\n每行輸入一條弧依附的頂點（先弧尾後弧頭）（如：v1v2）:\n");
	fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
	int i = 0, j = 0;
	for(int k = 0; k < G.arcnum; k++){
		scanf("v%dv%d",&v1, &v2);
		fflush(stdin);//清除殘餘後，後面再讀入時不會出錯
		i = locateVex(G, v1);//弧起點
		j = locateVex(G, v2);//弧終點
		
		//採用“頭插法”在各個頂點的弧鏈頭部插入弧結點
		ArcNode *p = (ArcNode *)malloc(sizeof(ArcNode));//構造一個弧結點，作為弧vivj的弧頭（終點）
		p->tailvex = i;
		p->tailNextarc = G.vexs[i].firstOut;
		G.vexs[i].firstOut = p;
		p->headvex = j;
		p->headNextArc = G.vexs[j].firstIn;
		G.vexs[j].firstIn = p;
	}
}
//列印十字連結串列
void printOrthogonalList(OLGraph G){
	printf("\n");
	for(int i = 0; i < G.vexnum; i++){
		printf("以頂點v%d為弧尾的弧有為：", G.vexs[i].data);
		ArcNode *p = G.vexs[i].firstOut;
		while(p){
			printf("v%dv%d ", G.vexs[i].data, G.vexs[p->headvex].data);
			p = p->tailNextarc;
		}
		printf("\n");
	}
	printf("\n");
}

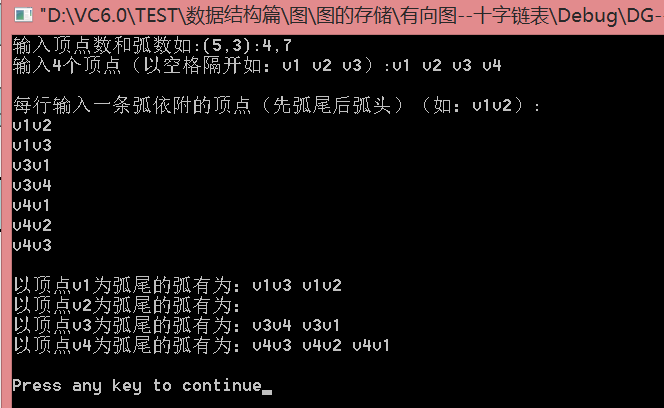
4.4演示

/*測試：
4,7
v1 v2 v3 v4

v1v2
v1v3

v3v1
v3v4

v4v1
v4v2
v4v3
*/
void main(){
	OLGraph G;
	createDG(G);
	printOrthogonalList(G);
}

相關推薦

資料結構(16)--圖的儲存及實現

參考書籍：資料結構（C語言版）嚴蔚敏吳偉民編著清華大學出版社         圖狀結構是一種比樹形結構更復雜的非線性結構。在樹狀結構中，結點間具有分支層次關係，每一層上的結點只能和上一層中的至多一個結點相關，但可能和下一層的多個結點相關。而在圖狀結構中，任意兩個結點之間都可

【資料結構】HashTable原理及實現學習總結

有兩個類都提供了一個多種用途的hashTable機制，他們都可以將可以key和value結合起來構成鍵值對通過put(key,value)方法儲存起來，然後通過get(key)方法獲取相對應的value值。一個是前面提到的HashMap，還有一個就是馬上要講解的HashTa

【資料結構】LinkedList原理及實現學習總結

一、LinkedList實現原理概述 LinkedList 和 ArrayList 一樣，都實現了 List 介面，但其內部的資料結構有本質的不同。LinkedList 是基於連結串列實現的（通過名字也能區分開來），所以它的插入和刪除操作比 ArrayList

C語言資料結構----棧的定義及實現

本節主要說的是資料結構中的棧的基本定義和實現的方式，其中實現的方式採用的是複用順序表和單向連結串列的方式。 一、棧的基本定義 1.棧是一種特殊的線性表，只能從固定的方向進出，而且棧進出的基本原則是：先進棧的元素後出棧。 2.老唐對棧頂棧底的定義： 棧頂：允許操作的一端。

資料結構：圖（鄰接表儲存 c++實現）

#include <iostream> #include <string> #include <queue> using namespace std; #define MAXVEX 10 #define INFINITY 0XFFFFF

資料結構作業——圖的儲存及遍歷（鄰接矩陣、鄰接表+DFS遞迴、非遞迴+BFS）

鄰接矩陣存圖 /* * @Author: WZY * @School: HPU * @Date: 2018-11-02 18:35:27 * @Last Modified by: WZY * @Last Modified time: 2018-11-0

演算法與資料結構基礎8：C++實現有向圖——鄰接表儲存

前面實現了連結串列和樹，現在看看圖。 連結串列是一對一的對應關係； 樹是一對多的對應關係； 圖是多對多的對應關係。 圖一般有兩種儲存方式，鄰接表和鄰接矩陣。 先看鄰接表。 鄰接表就是將圖中所有的點用一個數組儲存起來，並將此作為一個連結串列的頭， 連結串列中儲存跟這個點相鄰的

演算法與資料結構基礎9：C++實現有向圖——鄰接矩陣儲存

鄰接矩陣的儲存比鄰接表實現起來更加方便，也更加容易理解。 鄰接矩陣就是用一個二維陣列matrix來儲存每兩個點的關係。如果兩個點m，n之間有邊，將陣列matrix[]m[m]設為1，否則設為0。 如果有權，則將matrix[m]n[]設為權值，定義一個很大或者很小的數(只要

資料結構3--棧（java實現棧的順序儲存）

1.棧      棧也叫堆疊，是一種限制只能在某一端進行插入和刪除操作的線性表                          

資料結構——關於圖的儲存中十字連結串列和鄰接多重表的理解和思考

有向圖的十字連結串列   對於有向圖來說，鄰接表是有缺陷的，關心了出度問題，想了解入度就必須要遍歷整個圖才能知道，反之，逆鄰接表解決了入度的情況。 把鄰接表與逆鄰接表結合起來，即有向圖的一種儲存方法十字連結串列(Orthogonal   List)。 我們重新定義頂點表結

資料結構 鄰接矩陣儲存圖的深度優先遍歷

練習6.1 鄰接矩陣儲存圖的深度優先遍歷 （20 point(s)） 試實現鄰接矩陣儲存圖的深度優先遍歷。 函式介面定義： void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ); 其中MGraph是鄰

演算法與資料結構(四) 圖的物理儲存結構與深搜、廣搜(Swift版)

開門見山，本篇部落格就介紹圖相關的東西。圖其實就是樹結構的升級版。上篇部落格我們聊了樹的一種，在後邊的部落格中我們還會介紹其他型別的樹，比如紅黑樹，B樹等等，以及這些樹結構的應用。本篇部落格我們就講圖的儲存結構以及圖的搜尋，這兩者算是圖結構的基礎。下篇部落格會在此基礎上聊一下最小生成樹的Prim演算法以及克魯

資料結構之圖的鄰接矩陣儲存方法

這段時間遇到了關於圖的問題，然後發現之前學過的內容都還給老師了，因此又看了一遍，做個彙總。 圖的定義： 圖G是由頂點的非空有限集合V與邊的集合E構成的，形式化定義如下： G = （V，E） 圖可以分為有向圖和無向圖。無向圖是指圖的每一條邊都沒有方向；有向圖是指圖的每一條邊都

【資料結構】圖的儲存結構

是否可以採用順序儲存結構儲存圖? 圖的特點：頂點之間的關係是m:n，即任何兩個頂點之間都可能存在關係（邊），無法通過儲存位置表示這種任意的邏輯關係，所以，圖無法採用順序儲存結構。 如何儲存圖? 考慮圖的定義，圖是由頂點和邊組成的，分別考慮如何儲存頂點、如何

資料結構：圖的儲存結構之鄰接矩陣

一、圖（Graph）是由頂點的有窮非空集合和頂點之間邊的集合組成，通常表示為：G（V，E），其中，G表示一個圖，V是圖G中頂點的集合，E是圖G中邊的集合。在圖中的資料元素，我們稱之為頂點（Vertex），頂點集合有窮非空。在圖中，任意兩個頂點之間都可能有關係，頂點之

資料結構，圖的鄰接矩陣建立，鄰接矩陣與鄰接表的交換，兩種表的輸出，過程用C++實現

/* 編寫一個程式algo8-1.cpp,實現不帶權圖和帶權圖的鄰接矩陣與鄰接表的互相 轉換演算法、輸出鄰接矩陣與鄰接表的演算法，並在此基礎上設計一個程式exp8-1.cpp 實現如下功能： 1）建立如圖有向圖G的鄰接矩陣，並輸出； 2）由有向圖G的鄰接矩陣產生鄰接表，並輸

【資料結構】圖（最短路徑Dijkstra演算法）的JAVA程式碼實現

最短路徑的概念最短路徑的問題是比較典型的應用問題。在圖中，確定了起始點和終點之後，一般情況下都可以有很多條路徑來連線兩者。而邊或弧的權值最小的那一條路徑就稱為兩點之間的最短路徑，路徑上的第一個頂點為源點，最後一個頂點為終點。圖的最短路徑的演算法有很多，本文主要介紹狄克斯特拉（

資料結構 鄰接矩陣儲存圖的深度優先遍歷

練習6.1 鄰接矩陣儲存圖的深度優先遍歷 （20 point(s)） 試實現鄰接矩陣儲存圖的深度優先遍歷。 函式介面定義： void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) ); 其中MGraph是鄰接矩

資料結構之圖的兩種儲存方式

第一種：鄰接矩陣 鄰接矩陣可以表示頂點之間的相鄰關係的矩陣，是一個n階方陣，可以用一個一維陣列來表示頂點資訊，用一個二維陣列來表示頂點之間的邊的聯絡以及權重 具體的程式碼如下： #include <stdio.h> #inc

資料結構之圖（鄰接表儲存，DFS和BFS遍歷）

     來看下面的一個簡單的圖，       那麼這樣的一個圖，我們應該用什麼儲存結構來儲存它呢？常用的是鄰接矩陣和鄰接表，這裡鄰接矩陣不做講解，如下所有程式碼都是以鄰接表作為儲存結構，所以這裡就只講解下鄰接表。那麼什麼是鄰接表呢？如何構造呢？       鄰接表是一