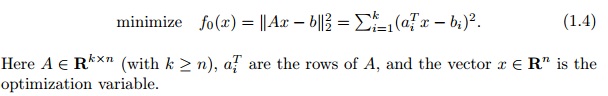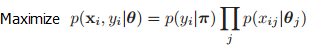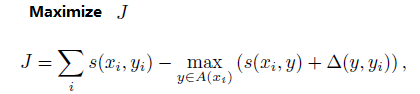從Andrew ng的公開課開始，機器學習的演算法我接觸到的也越來越多，我覺得機器學習演算法和傳統演算法的最大不同就是:不會要求一個問題被100%求解，也就意味著不會有完美的解法，這也是著名的“Essentially, all models are wrong, but some are useful.”所表達的意思。正因為如此，機器學習演算法往往不會有一個固定的演算法流程，取而代之的把問題轉化為最優化的問題，無論是ML(maximum likelihood),MAP(Maximum a Posterior)和EM(Expectation Maximization)，都是這樣的。

     然後用不同的方法來優化這個問題，得到儘量好的結果，給人的感覺就像是一個黑盒，實際使用中需要不斷地調參實驗，但倘若你能理解好演算法，至少能讓這個盒子透明一點，這也是機器學習演算法確實需要使用者去理解演算法的原因

     這樣一來，閱讀各類書籍和paper也就在所難免了，甚至去閱讀程式碼以至於實現加深理解，對於實際使用還是有很大的好處的，因為不是100%求解問題，所以面對不同的應用場景，想要達到最好的效果都需要加以變化。本文記錄了一點自己學習的心得，私以為只要你能對演算法有一種說得通的解釋，就是OK的，不一定要去深挖其數學上的證明(表示完全挖不動啊…………>_<)

=====================================================================

O.  目的

     之前說到機器學習演算法常常把問題轉化為一個最優化問題，理解這個最優化問題的目的能很好地幫助我們理解演算法，比如最簡單的最小二乘法(Least-squares)：

     (這裡的x是引數，和一些機器學習的常用表示裡面有出入)

     好多機器學習入門書都是從最小二乘開始引入的，其實這是線性代數(還是概率統計?囧rz)的課本內容嘛。

     理解上式應該非常簡單吶，括號內的就是目標值和與測試的差，取平方之後抹掉正負，而該式是要最小化這個東西，那麼這個優化問題的“目的”

     當然這是最簡單的一個例子了，我們接著看樸素貝葉斯分類器的優化目標:

     (這裡xi,yi是訓練集，π和θ是引數)

      無論他後面怎麼變化，用了什麼優化方式，該演算法的目的就是在訓練集上最大化這個東西，只不過對於樸素貝葉斯來說，它加入了非常強的假設來簡化問題而已。

      然後樸素貝葉斯用了一系列的引數來描述這個需要優化的概率值，為了達到目的還是用了log來變換一下，但對於你來說，只需要記住他的“目的”，就可以很容易地理解演算法了。

一.  趨勢

        接下來要講的是"趨勢"，廣義上來說和目的是一回事，但演算法的優化目標的一些部分是與演算法總體目的相對分割的，比如一些正則化(regularization)的項，這些項對於演算法實際使用效果往往有著重大影響，但並不絕對大的方向(目的)，所以“趨勢”我們單獨開 一章來講。

        我們還是從最簡單的 L2-norm regularization 來開啟這個話題吧，把這個項加到最小二乘後面:

        雖然也能把該式表示為標準的最小二乘結構，但對理解演算法並無幫助，我們不這樣做。

        可以看到該式的第二項是想要引數的平方和，而整個是Minimize的，所以直觀來說就是想要學到的引數的絕對值越小越好，這就是我理解的“趨勢”

        可是為什麼讓引數平方和越小能防止over-fitting呢？這裡就有很多解釋了，比如加入該項是對資料的原始分佈加了個高斯分佈作為先驗(有證明的貌似)，但像我這種數學渣渣還是走intuition的方向吧，這樣理解：(這是Convex Optimizition課上提到的，我也不知道是否是對的，但能夠說通)

        我們得到的訓練資料是有測量誤差的，記為delta,引數為x，要優化的為:||Ax-y||，其實是||(A'+delta)x-y||=||A'x-y+delta*x||：

        所以引數x的值越小，誤差delta對於模型的影響就越小，所以能增加模型的泛化能力。

二.  還是趨勢

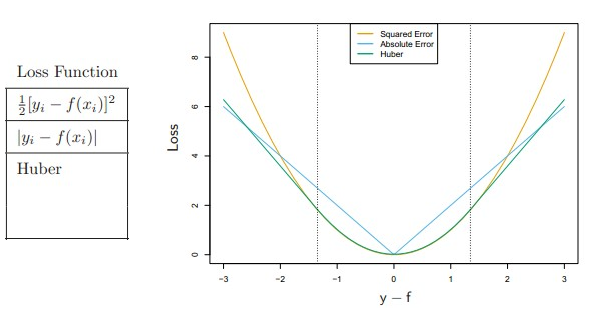
        再寫上面一章就略長了，新開一段…………還是講趨勢，對於最小二乘，其實是Loss function一種，也就是我們想要最小化的東西，除此之外還有其它的一些Loss function，其選擇同樣也會影響演算法的效果。(這裡的xi和yi又是訓練集了，不是引數，略亂，見諒)

         上面的Huber是在一個閥值內是二次的，閥值外則是線性的

         這能體現什麼趨勢呢？可以明顯看到，對於偏差很大的case來說（|y-f|>2），平方項【1】的要比絕對值【2】的懲罰大不少，這意味著【1】對於極端outlier的容忍能力更差，離太遠了簡直是沒法承受的，對演算法帶來的影響就是要去滿足這個outlier，從而帶來一些問題。而在一定閥值以內的時候，平方項【1】的懲罰卻比絕對值【2】還要小。綜合來看，相對於絕對值，平方項的趨勢就是去滿足outlier,把絕大多數訓練資料的loss降低到夠小的範圍即可。(略繞，但應該不難理解)

         Huber的優點就是既對outlier有容忍力(大於閥值其增長是線性的)，又不至於全是線性增長，對誤差重要程度沒有太大區分(小於閥值是二次的)，所以Boyd在公開課上就說:對於絕大多數使用二次Loss function的地方來說，換用Huber基本上都會有更好的效果

三.  一個複雜點的例子

        前段時間組內讀書會有大大分享了一片論文，開始讀著無比順暢，但就是到了其中一步無法理解，考慮了很久，就用我的“趨勢”分析法^_^理解了下來，這裡就不給上下文了，論文叫<Learning Continuous Phrase Representations and Syntactic Parsing with Recursive Neural Networks>，有興趣可以去看，我現在單把那一個公式提出來分析其目的(趨勢)

        其中的s()是表示傳入引數的一個得分值，A( xi )表示對於xi來說所有可能的 y 結構，Δ(y,yi) 是對結構 y 和 yi 相異程度 的懲罰專案，Δ( yi , yi)=0

        這個式子很難理解就在於maximize裡還減去一個max，而且max裡面還不是norm的結構，乍一看是和以前見過的有巨大差異

        但仔細思考其實可以發現，A( xi )之中是有 yi 的，即訓練資料。所以 max() 那一項最小的取值就是 s( xi,yi )，不會比這個小，那這個式子的目的是什麼呢？

        作者堅定地認為訓練資料就是最好最正確的，其得分就該是最高的，所以一旦max項裡面選出來的是比 s( xi,yi )大的，就對其進行懲罰，最後該式的目的就是在所有 xi 可能對應的結構 y 中，訓練資料 yi 應該是最好的。與此同時加入Δ項，是為了使與 yi 結構更接近的 y 得分更高( 這個這麼理解：演算法給所有結構加了一個上限在那，超過了就砍頭，那麼Δ(y,yi)值越小，剩下的可喘息的部分就越大，也就是得分就越高)

        這個式子和經驗裡看到的有很大差異，但通過分析他的目的和趨勢，就可以較好地理解演算法和裡面一些引數的意義，從而到達我們學習演算法的目的

四.  尾巴

        本來打算磨好久的，居然幾個小時就搞定了，真是順利啊

        這是我理解演算法的一點小心得，可能會有錯的地方，求指正啊~~~~~

       【ref】:

        【1】.《Convex Optimization 》（Byod）

        【2】.《Machine Learning - A Probabilistic Perspective》

        【3】.《TheElementsofStatisticalLearning》

        【4】:Learning Continuous Phrase Representations and Syntactic Parsing with Recursive Neural Networks