關聯規則演算法Apriori以及FP-growth學習
關聯規則演算法Apriori以及FP-growth學習
最近選擇了關聯規則演算法進行學習,目標是先學習Apriori演算法,再轉FP-growth演算法,因為Spark-mllib庫支援的關聯演算法是FP,隨筆用於邊學邊記錄,完成後再進行整理
一、概述
關聯規則是一種常見的推薦演算法,用於從發現大量使用者行為資料中發現有強關聯的規則。常用於回答“那些商品經常被同時購買”的問題,最經典的用途就是“購物籃分析”,也就是“尿布和啤酒”,用於在商場中發現顧客經常一起購買的商品,從而優化貨物擺放。
從大規模資料集中尋找物品間的隱含關係被稱作關聯分析(association analysis)
二、關聯分析
關聯分析是在大量資料中尋找存在關係的任務。這些關係可能有兩種
●頻繁項集
●關聯規則
頻繁項集(frequent item sets)是經常出現在一塊兒的物品的集合,關聯規則(association rules)暗示兩種物品之間可能存在很強的關係。
舉例說明,給出某店銷售清單:
| 訂單號 | 商品 |
| 1 | 豆奶、萵苣 |
| 2 | 萵苣、豆奶、葡萄酒、甜菜 |
| 3 | 豆奶、尿布、葡萄酒、橙汁 |
| 4 | 萵苣、豆奶、尿布、葡萄酒 |
| 5 | 萵苣、豆奶、尿布、橙汁 |
●頻繁項集指經常出現在一起的集合,例如訂單中的{葡萄酒、豆奶、尿布},或是{豆奶、尿布},根據頻繁項集我們可以推測,購買了豆奶的人,很有可能會同時購買尿布,為了度量這種推測的可靠性,引入兩個標準,支援度和置信度。
●支援度(Support)
支援度表示item-set在所有的事件N中出現的頻率,計算公式為
![]()
例如在上述示例中,{尿布、豆奶}的支援度為3/5=0.6。五條事務中有三條事務包含尿布和豆奶
在實際使用中,通常會設定一個最低支援度(minimum support),將大於或等於最低支援度的X稱為頻繁的item-set。
●置信度(Confidence)
置信度表示規則 X ⇒ Y 在所有事務中出現的頻率。他的含義是滿足X的條件下,同時滿足Y的事務佔所有事務的比例:
![]()
在示例中X ⇒ Y體現在:購買尿布的人中,同時還會購買豆奶
示例中,{尿布、豆奶}的置信度為0.6/0.6=1。
同樣使用中我們會設定一個最低置信度,>=最低置信度的規則我們認為是有意義的
三、Apriori原理
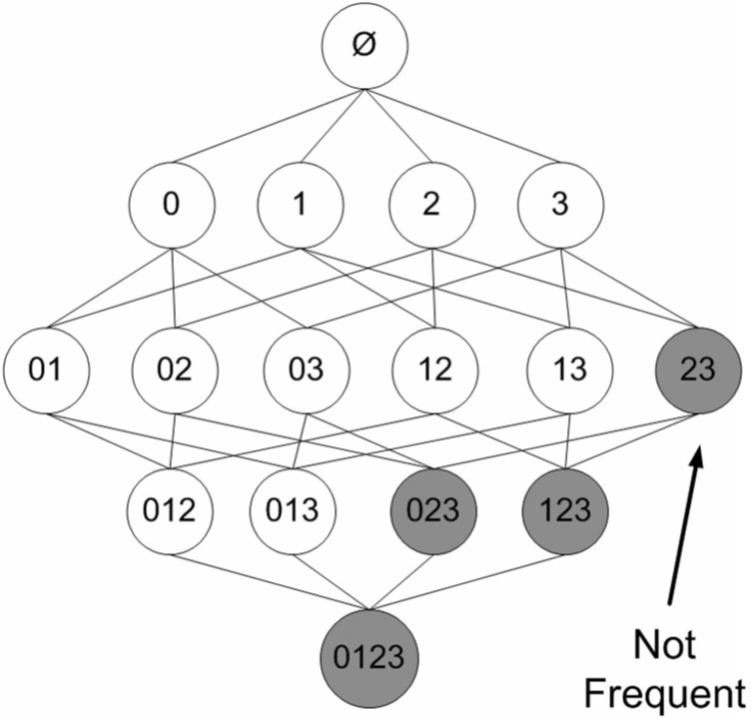
假設一家店有商品1、2、3、4,圖中顯示了商品所有可能的組合

對於單個項集的支援度,我們可以通過遍歷的方式來計算,但是當商品數N過大時,資料集共有
2N−1種項集組合,進行遍歷效率不高。
因此基於一種Apriori原理,即說如果某個項集是頻繁的,那麼它的所有子集也是頻繁的,以及他的逆否命題如果一個項集是非頻繁的,那麼它的所有超集也是非頻繁的。
例如在下圖中,已知陰影項集{2,3}是非頻繁的。由此我們就可以知道項集{0,2,3},{1,2,3}以及{0,1,2,3}也是非頻繁的。也就是說,一旦計算出了{2,3}的支援度,知道它是非頻繁的後,就可以由此排除{0,2,3}、{1,2,3}和{0,1,2,3}。
四、Apriori演算法流程
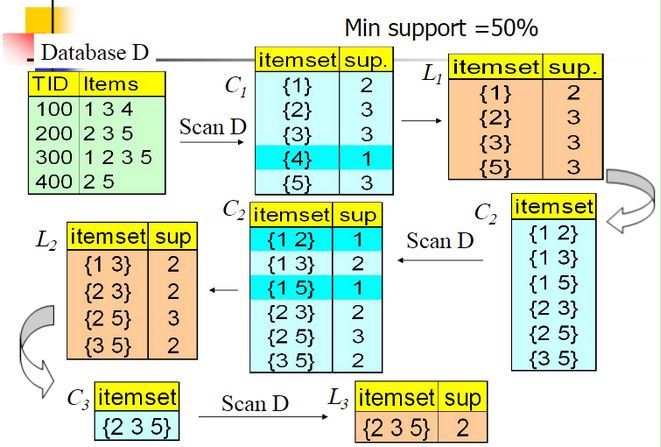
如圖,給定訂單Database D,Apriori的掃描流程:
1.掃描所有訂單的所有商品,生成候選頻繁1項集C1,包含所有的五個資料並計算五個資料的支援度。
2.進行剪枝,資料{4}的支援度只有25%被剪掉,得到頻繁1項集L1為1235
3.選出只有最後一位不同的集合求並集,連線生成頻繁2項集C2,包括12,13,15,23,25,35六組,第一輪迭代結束
4.第二輪迭代,掃描資料集計算C2的支援度,繼續剪枝,刪除12和15得到頻繁2項集L2
5.對L2進行連結,剪枝。。。。。
6.最終得到頻繁三項集235
流程總結:
輸入:資料集合D,支援度閾值α
輸出:最大的頻繁K項集
過程:
1)掃描整個資料集,得到所有出現過的資料,作為候選頻繁1項集。k=1,頻繁0項集為空集。
2)挖掘頻繁k項集
a) 掃描資料計算候選頻繁k項集的支援度
b) 去除候選頻繁k項集中支援度低於閾值的資料集,得到頻繁k項集。如果得到的頻繁k項集為空,則直接返回頻繁k-1項集的集合作為演算法結果,演算法結束。 如果得到的頻繁k項集只有一項,則直接返回頻繁k項集的集合作為演算法結果,演算法結束。
c) 基於頻繁k項集,連線生成候選頻繁k+1項集。
3) 令k=k+1,轉入步驟2。
Apriori演算法Aprior演算法每輪迭代都要掃描資料集,因此在資料集很大,資料種類很多的時候,演算法效率比較低。
