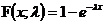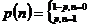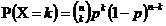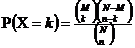1.離散概率分佈
1)泊松分佈
描述是單位時間（面積）內隨機事件發生的次數。
【滿足條件】
a.平穩性：任意時間區間內，事件發生k次的概率只依賴於區間長度
b.獨立性：在不重疊的時間段內，事件的發生是相互獨立的
c.小概率事件
【概率函式】

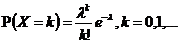
期望和方差均為λ
【應用場景】
a.某一服務設施在一定時間內到達的人數，接待人數
b.電話交換機接到呼叫的次數
c.機器出現的故障數
λ表示隨機事件的平均發生率。泊松分佈的k表示實際發生次數

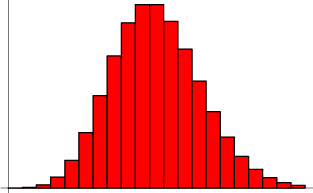
在頻率附近，時間發生的概率最高，兩邊對稱下降。
2)伯努利分佈
有兩種可能的結果。1表示成功，出現的概率為p。0表示失敗，出現的概率為q=1-p。
【滿足條件】
a.一次實驗，兩種結果
【分佈律】

期望為p，方差為p(1-P)
3)幾何分佈 X ~ G(p)
在n次伯努利試驗中，試驗k次才得到第一次成功的機率。
【滿足條件】
a.伯努利實驗
a-1. 每次試驗中只有兩種可能的結果，而且兩種結果發生與否互相對立;
a-2. 每次實驗相互獨立，與其它各次試驗結果無關
a-3. 事件發生與否的概率在每一次獨立試驗中都保持不變。
b.前k-1次都失敗，第k次才成功
【概率函式】

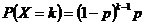
期望為，方差為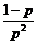
【應用場景】

4)二項分佈 X ~ B(n, p)
重複n次獨立的伯努利試驗，成功次數為k。
【滿足條件】
a.伯努利實驗
b.共有n次實驗，其中k次成功
【概率函式】

期望為np，方差為np(1-p)
【應用場景】
a.拋硬幣結果出現的概率
b.患者治療後的結局（治癒/未治癒）
5)負二項分佈X ~ NB(r, p)
滿足伯努利分佈，重複實驗到出現r次成功為止。
【滿足條件】
a.伯努利實驗
b.共有k次實驗，前k-1次實驗成功了r-1次，第k次試驗為第r次成功
【概率函式】
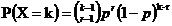，k = r+1, …
期望為r/p，方差為
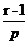
r = 1時即為幾何分佈
【應用場景】

6)超幾何分佈 X ~ H(N, n, M)
不放回抽樣。總共N件物品，包含M件指定物品，抽出n個物品中，指定物品為k的概率分佈。已經知道某個事件的發生概率，判斷從中取出一個小樣本，該事件以某一個機率出現的概率問題。
【滿足條件】
a.不放回抽樣
【概率函式】

期望為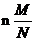，方差為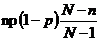
【應用場景】
a.產品抽檢

2.連續型分佈
1)均勻分佈 X ~ U[a, b]
【滿足條件】
【應用場景】
a.投票，每一票具有相同的效力
【概率函式】
離散均勻分佈：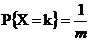
連續型的概率密度函式：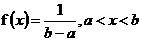
期望為(a+b)/2, 方差為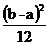
2)正態分佈 X ~ N()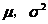
【滿足條件】
【應用場景】
b.近似服從正態分佈的醫學現象。比如同性別、同年齡兒童的身高和體重，同性別健康成人的紅細胞數、血紅蛋白含量、脈搏數等。在這類情形下，利用正態分佈可以很容易地確定其數值出現在任意指定範圍內的概率，尤其是醫學參考值範圍的估計。
c.實驗中的測量誤差一般也是服從正態分佈的，利用這一點，可以準確地進行誤差分析和質量控制
【概率密度函式】

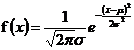
期望為μ，標準差為σ
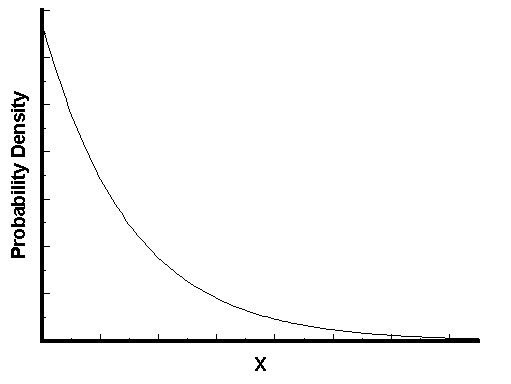
3)指數分佈X~E()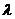
指數分佈是事件的時間間隔的概率。
指數函式具有無記憶性。即當s, t≥0時，有P(T>s+t|T>t) = P(T>s)。即，如果T是某一元件的壽命，已知元件使用了t小時，它總共使用至少s+t小時的條件概率，與從開始使用時算起它使用至少s小時的概率相等。
【滿足條件】
【應用場景】
a.表示獨立隨機事件發生的時間間隔，如旅客進機場的時間間隔，上下班簽到的時間間隔，嬰兒出生的時間間隔，網站訪問的時間間隔。
b.電子產品壽命的分佈
c.機器平均故障時間，機器或系統的失效分佈模型
【概率密度函式】

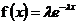
λ為單位時間內發生某件事的次數
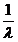
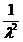
期望為，標準差為
【分佈函式】