2815 Mod Tree 【高次不定方程 + 擴充套件 BSGS + 板子】
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7143 Accepted Submission(s): 1750
Problem Description
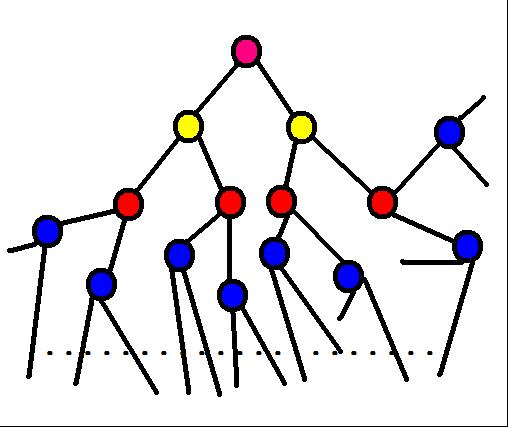
The picture indicates a tree, every node has 2 children.
The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
Now out problem is so easy, give you a tree that every nodes have K children, you are expected to calculate the minimize depth D so that the number of nodes whose depth is D equals to N after mod P.
Input
The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)
Output
The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”
Sample Input
3 78992 453
4 1314520 65536
5 1234 67
Sample Output
Orz,I can’t find D!
8
20
題意: 一個樹上,每個節點有k個孩子,給你一個p和N ,且不保證p為素數
分析: 這是一個板子題,如果p為素數的時候,是BSGS,這裡要用到擴充套件BSGS,原理看下這裡吧
就當做個板子吧
參考程式碼
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <map>
#include <cmath>
#include <unordered_map>
using namespace std 手寫hash實現BSGS程式碼(僅記錄)
//程式碼不是擴充套件BSGS,是普通的BSGS
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cmath>
#define ll long long
#define MEM(a,b) memset((a),(b),sizeof(a))
using namespace std;
const int N = 499991;
ll a,p,b;
bool Hash[N];
int val[N];
int id[N];
void Insert(int i,ll num){
ll k = num%N;
while(Hash[k] &&val[k] != num){k = (k+1)%N;}
if(!Hash[k]){
Hash[k] = true;
val[k] = num;
id[k] = i;
}
}
void egcd(ll a,ll b,ll& d,ll& x,ll &y){
if(!b){d = a,x = 1;y = 0;}
else{egcd(b,a%b,d,y,x);y -= x*(a/b);}
}
int found(ll num){
ll k = num%N;
while(Hash[k] && val[k]!=num){k = (k+1)%N;}
if(Hash[k])return id[k];
return -1;
}
int BSGS(){
MEM(Hash,false);
MEM(val,-1);
MEM(id,-1);
ll m = ceil(sqrt(p));
ll M = 1;
for(int i = 0;i < m;i++){
Insert(i,M);
M = a*M%p;
}
ll t = 1;
for(int i = 0;i < m;i++){
ll x,y,d;
egcd(t,p,d,x,y);
x = x*b%p;
x = (x+p)%p;
int s = found(x);
if(s != -1)return s+m*i;
t = t*M%p;
}
return -1;
}
int main(){
while(cin>>p>>a>>b){
int ans = BSGS();
if(ans == -1)cout<<"no solution"<<endl;
else cout<<ans<<endl;
}
return 0;
}
