前言

這個上下界網路流是一個以前我這個巨弱弱想都不敢想的一個東西。
然而，最近一次比賽居然考了這個東東。
於是整個機房掀起了破爛學上下界網路流的熱。
那麼我也來學學。

預備知識

要懂得很多很多的網路流知識比如最大流這種基礎的。
當然，還有一個流量的平衡條件：
$\sum f(u,$

x ) = ∑ f ( x , v )

\sum f(u,x)=\sum f(x,v)
這個條件可以用來判斷可行性。為什麼呢？
這裡有一條定義，自己看吧（其實畫個圖更容易理解）
——————————————————————————
在圖中有一條從 s 到 t 的路徑, 這條路徑上起點 fo−fi=f, 終點 fi−fo=f， 其他的點 fi==fo, 並且所有的邊的當前流量小於等於最大流量.(其中 fi 代表流入流量, fo 代表流出流量)
——————————————————————————

正題

實際上，這個上下界網路流是有很多種型別的，我一一來闡述。

無源匯上下界可行流

設，上界為up，下界為down
建圖方法
我們可以考慮建一個新圖。
首先弄一個新的源點和匯點ns和nt。
然後，對於原圖中每條(u,v)的邊，建u→v流量為up-down
然後，我們設一個d(x)表示x流入x點的邊的下界和，減去流出x點的邊的下界和。
當，d(x)>0則連ns→x流量為d(x)的邊。
否則，d(x)<0則連x→nt流量為-d(x)的邊。
我們不妨稱後面這兩條邊為附加邊。

流程
從源點流到匯點，當每條附加邊已經流滿的時候，則可以確定這個圖可行。

證明
我們設一個g(u,v)表示實際流量f(u,v)=up(u,v)+g(u,v)
那麼0<=g(u,v)<=up(u,v)-down(u,v)
如果我們不加附加邊，這顯然是錯的。
那麼我們看看附加邊的作用：
$因為要滿足平衡條件\sum f(u,x)=\sum f(x,v)$
$那麼\sum down(u,x)+g(u,x)=\sum down(x,v)+g(x,v)$
$\sum down(u,x)-\sum down(x,v)=\sum g(x,v)-\sum g(u,x)$
$因為d(x)=\sum down(u,x)-\sum down(x,v)$
$d(x)=\sum g(x,v)-\sum g(u,x)$
當，d(x)>0時，那麼 $d(x)+\sum g(u,x)=\sum g(x,v)$
當，d(x)<0是，那麼 $-d(x)+\sum g(u,x)=\sum g(x,v)$
圖長這樣——

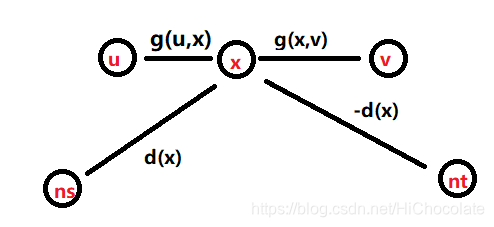
這樣就可以保持新圖的平衡條件。

有源匯上下界可行流

建圖方法
由於原圖中，只有源點與匯點不滿足平衡條件，於是強行在匯點連條無線大流量個邊到源點即可。
其餘同上。
流程
同上。
證明
同上。

有源匯上下界最小流

建圖方法
同“無源匯上下界可行流”
流程
先在這個圖上判斷可行性。
此時，答案即為超級源到超級匯的最大流。
證明
由於補流與分流是流每條邊的下界的，一旦達到下界後，就代表可行。
此時，下界的答案即為補流與分流的流量。
但是光到達下界不行，還有可以到達上界到下界之間的答案。
於是乎，我們就把原來每條邊的最大流加入答案即可。

有源匯上下界最大流

建圖方法
同“有源匯上下界可行流”
流程
先在這個圖上判斷可行性。
此時，超級源到超級匯的補流與分流的流量先加入答案。
然後，我們把超級源以及超級匯刪掉，並且把t→s的邊也刪掉。
再做一遍最大流，即可。
證明
類似於上面。

費用流+上下界網路流

注，這裡費用流是最小費用最大流，其他什麼流應該是類似的思想。
建圖方法
首先弄一個新的源點和匯點ns和nt。
然後，對於原圖中每條(u,v,cost)的邊，建u→v流量為up-down，費用為cost
然後，我們設一個d(x)表示x流入x點的邊的下界和，減去流出x點的邊的下界和。
當，d(x)>0則連ns→x流量為d(x)，費用為0的邊。
否則，d(x)<0則連x→nt流量為-d(x)，費用為0的邊。
當然，這個圖是有源點與匯點的，那麼連匯點到源點流量為無限大，費用為0即可。
流程
直接按照費用流的方式跑即可，因為答案統計是和上面一樣的。
別跟我說你不會費用流
證明
由於這個圖已經奇妙地轉化成了普通圖，所以不用說了吧。
運用
這個費用流只用於滿足流量限制後的最小費用，不滿足最大流。

優化

至此，上下界網路流的一些基本建圖方法已經講完了。
而且，經過我的一些觀察，找到了兩種建圖方法——
一種是我上述的方法，在點少邊多的圖藥效奇佳，而且好理性證明。
另一種是網上學到，在點多邊少的圖藥效奇佳，但是我不會理性證明，只會很感性地理解。（畫圖）
在此口胡一下在“無源匯上下界可行流”的建圖方法

• 建立超級源與超級匯。
• 對於一條邊(u,v)，建從v→u流量為up-down的邊。（注意是v→u）
• 然後建ns→v流量為down的邊。
• 然後建u→nt流量為down的邊。
• 之後直接求即可。

這個可以感性理解。
我們看到原來的u→v，由於下界是down，那麼當這條邊流過了down之後，相當於u失去down的水，v得到down的水，剩下的是up-down的水。
這樣建圖就可以模擬上述過程。

當然，也可以在最大流那優化。
如果你會sap、dinic之類的優秀演算法，是可以優化很多。
如果你會把這sap與dinic兩演算法的優秀之處結合起來，也是可以優化很多。
對於費用流，可以打zkw使得程式跑得更快。
當然，如果你打預流推進或高標，時間會降得更多。

題外話

至於題目，網上一大堆。
至於板子，主要就是建圖方式。