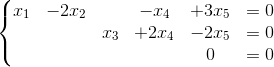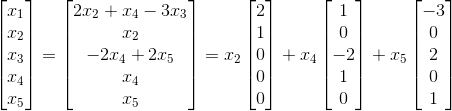線性代數複習四——矩陣的維數和秩
阿新 • • 發佈:2018-12-30
說明:以後前一部分主要講各種定義以及定理,用題目對定理來進行說明則放到後一板塊
定義: 中的一個子空間是
中的集合H,具有以下三個性質:
a. 零向量屬於H
b. 對H 中的任何向量u和v,u+v屬於H
c. 對H中任意向量u和數c,c u屬於H
即子空間對加法和標量乘法是封閉的
僅含零向量的子空間稱為零子空間
中子空間H 的一組基是H 中一個線性無關組,它生成H
矩陣A的列空間的A的各列的線性組合的集合,記作 Col A
矩陣A的零空間是齊次方程的所有解的集合,記作 Nul A
當線性方程組寫成的形式,Col A就是所有事方程有解的向量b的集合
矩陣A的主元列構成Col A的基
方程
非零子空間H 的維數,用dim H 表示,是H 的任意一個基的向量個數,零子空間的維數定義為零
矩陣A的秩(rank A)是A的列空間的維數,因為A的主元列形成Col A的一個基,A的秩正好是A的主元列的個數
秩定理:如果一個矩陣A有n列,則 rank A+ dim Nul A = n
最後接著上次最後給出的定理繼續給出一些等價命題
設A為矩陣,則下列命題是等價的:
m. A的列向量構成的一個基
n. Col A=
o. dim Col A=n
p. rank A=n
q. Nul A={0}
r. dim Nul A=0
求的零空間的基
首先把方程的解寫成引數向量的形式
通解為為自由變數
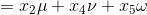
生成Nul A
注:設,雖然H 中的點也在
中,但它構成的是一個平面,對映
是H 和
之間保持線性組合關係的一一對應對映,我們稱這種對映是同構的且H 與
同構,即若矩陣A是3x5的,有三個主元列,則Nul A
這一講就到這裡,我們下次繼續~