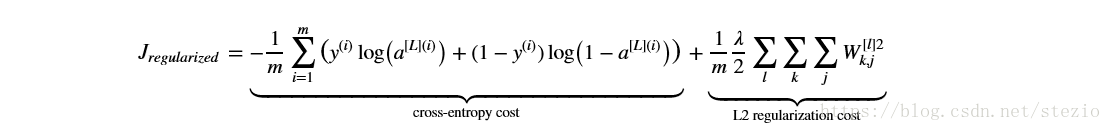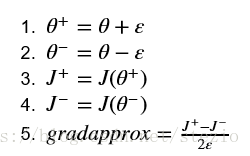改善深層神經網路week1學習筆記
1.Initialization
Zero initialization
即初始化為0。如果將w權重矩陣和b偏置矩陣都使用Zero initialization則會產生以下的結果:
演算法對每個測試樣裡都會輸出0,因此準確率在0.5左右,與隨機猜測無異。總體來說,因為沒有“打破對稱性”,每個神經元都做著一樣的事情,所以說會產生如上結果。一般地,將b零初始化,w隨機初始化。
Random initialization
即隨機初始化np.random.randn(..,..) 。
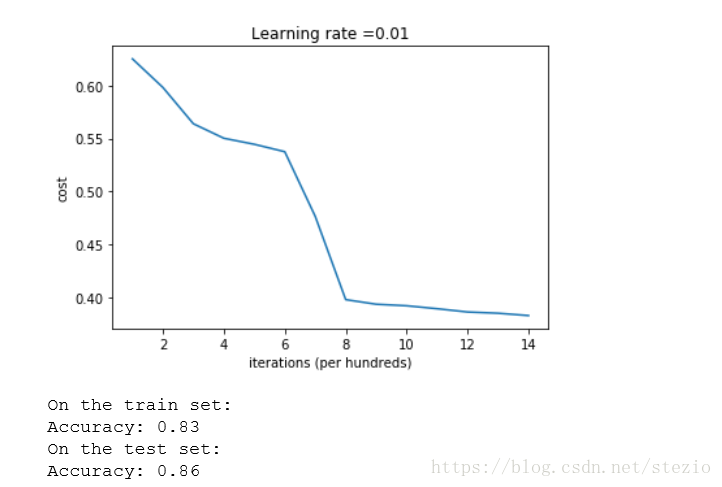
作業中將權重矩陣W採用了np.random.randn(..,..) * 10的方法進行初始化,結果如下:
由於初始權重較大損失開始較大,糟糕的初始化可能會導致梯度爆炸或者梯度消失,進而減緩演算法速度,初始化過大的權重也會減緩演算法速度。
He initialization
該方法適用於ReLU activation,相較於隨機初始化,本方法在後面乘以程式碼如下:
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * (2./layers_dims[l-1])**0.5
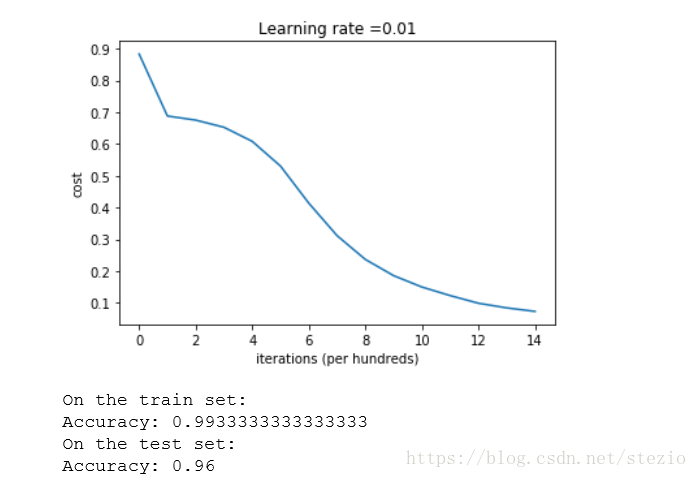
執行結果:
這也是本次作業中推薦使用的初始化方法。
2.Regularization
正則化為了處理過擬合的情況,在模型過於複雜時懲罰模型的複雜度
L2 Regularization
方法如下:
即在原來的cost後面加上了一個L2正則cost。當正則化因子 設定的足夠大的情況下,為了使代價函式最小化,權重矩陣
就會被設定為接近於0的值,則相當於減小了很多神經元的影響。
假設神經元中使用的啟用函式為 ,在加入正則化項後:
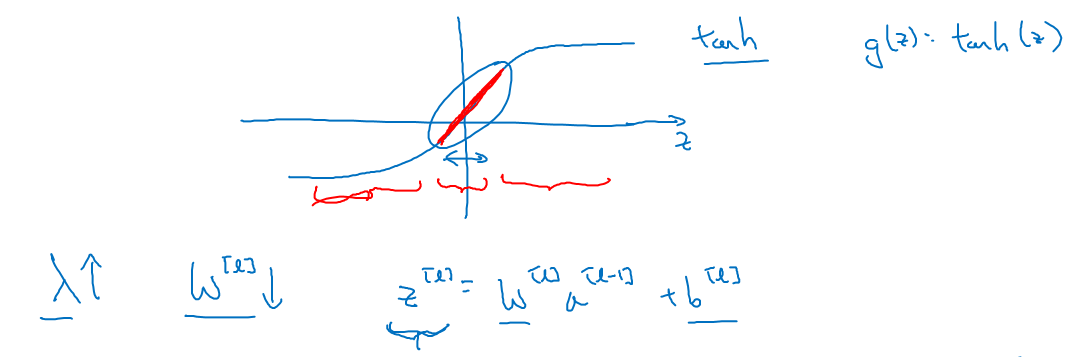
當 增大,導致
減小,
便會減小,由上圖可知,在
較小的區域裡,
函式近似線性,所以每層的函式就近似線性函式,整個網路就成為一個簡單的近似線性的網路,從而不會發生過擬合。
L2 regularization 是決策邊界更加平滑,如果過大,可能會造成邊界過於平滑而導致高偏差。
L2 regularization基於權重較小的模型比權重較大的模型工作效果更好這一觀點,因此在cost中採用平方項來使得權重取較小的值。
Dropout
該方法在每一次迭代中隨機關閉一些神經元來減少神經元的影響,編碼中採取了一個mask矩陣D來實現。利用D與A相乘來消除一部分神經元的影響,同時注意要對未被消除影響的神經元進行規模復原。編碼如下:
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
### START CODE HERE ### (approx. 4 lines)
D1 = np.random.rand(A1.shape[0], A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1<keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1*D1 # Step 3: shut down some neurons of A1
A1 = A1/keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
值得注意的是:dropout只用於訓練集,要在前向傳播和後向傳播中同步運用。
Dropout 缺點:dropout的一大缺點就是其使得 Cost function不能再被明確的定義,以為每次迭代都會隨機消除一些神經元結點,所以我們無法繪製出每次迭代 下降的圖。
另外,regularization方法會導致訓練集準確率下降,因為它限制了過擬合能力,但是會在測試集上有更好表現。
3.Gradient Checking
這裡主要是講的檢驗梯度的方法。這裡給出了一個變數gradapprox,用了雙邊逼近的原理,計算方法如下:
然後將gradapprox與後向傳播算出的grad計算誤差:
誤差低於一定的閾值則判定為正確。
至於作業中估計設定錯誤來造成梯度檢驗錯誤的地方在這裡:
把這個莫名其妙的4改成1就行了。。。
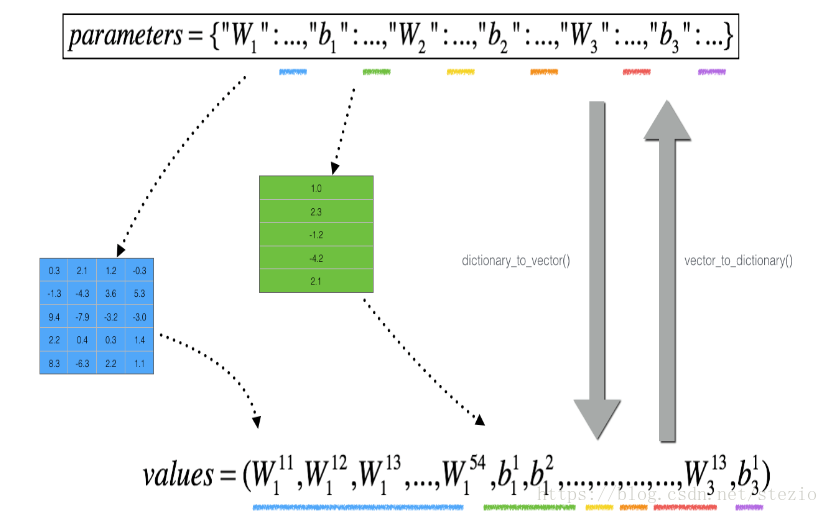
值得一提的是作業中有個定義好的函式,對parameter進行操作時得到的結果示意圖如下:
這是作業給出的示意圖,但是實際結果是下方的values為(num_parameters, 1)的矩陣,如下:
這一點作業中似乎沒有說的清楚,所以在後面計算時,theta實際上是包含所有引數的列為1的矩陣,即對所有引數都單獨進行了
的運算,然後進行向量的誤差計算。