概念

一句話概括：通過對引導影象對線變換，結合區域性線性模型，對原始影象進行濾波處理的演算法。

區域性線性模型

該模型認為，某函式上一點與其鄰近部分的點成線性關係，一個複雜的函式就可以用很多區域性的線性函式來表示，當需要求該函式上某一點的值時，只需計算該點線性函式的值並做平均即可。

應用於影象

假設在一個區域性視窗內，滿足一個線性關係
I 引導影象
q 濾波後的影象
p 原始影象
引導影象做線性變換之後，要與原始影象儘量接近，且模型儘量簡單。
1. 假設影象是一個二維函式，且輸入輸出在一個二維視窗內滿足線性關係：

qi=akIi+bk,∀i∈ωk
其中q是輸出畫素的值，I是輸入影象的值，i和k是畫素索引，a和b是當視窗中心位於k時該線性函式的係數。輸入影象不一定是待濾波影象，也可是是其他影象即引導影象，這也是稱為引導濾波的原因。對上式兩邊取梯度，得：
∇

q=a∇I
即當輸入影象I有==梯度==時，輸出q也有類似的梯度，因此引導濾波有==邊緣保持特性==。
2. 求線性函式的系統，即線性迴歸。目標函式讓擬合函式的輸出值和真實值p之前差距最小，即\
// 建立模型的一般套路：==min（經驗風險+正則項）==
E(ak,bk)=∑i∈ωk((akIi+bk−pi)2+εa2k)
其中p待濾波的影象，ε防止係數a過大。
最小二乘(平方)法求解：

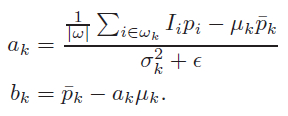
一個畫素會被多個視窗包含，即==每個畫素由多個線性函式描述==。因此，某一點的輸出值時，主需要將所有包含該點的線性函式平均即可，如下：

qi=1|ω|∑k:i∈ωk(akIi+bk)=a¯i

Ii+b¯i
其中w_k是所有包含畫素i的視窗，k是這些視窗的中心位置。

功能

• 平滑
• 去噪
• 影象去霾
• 影象增強

參考論文：Guided Image Filtering
拓展閱讀：最小二乘法