參考：

1. Directional statistics（Mardia）P14-19&29-30&47-50;

2. Biostatistical Analysis（2009 Zar）-5th edition P614-617;

3. CircStat: A MATLAB Toolbox for Circular Statistics（Philipp Berens）;（這是一個MATLAB中實現的計算方向資料的一個工具包）

以上文獻如有需要，可留下郵箱分享與你。

正文：

       最近因為做風的研究，需要衡量風向的一致性，就想轉化到求角度的標準差。但是，當你去算得時候你就會發現，角度的標準差與平常的我們所算的標準差是不一樣的。為行文方便，在本文中我把類似角度這樣的資料（多是週期數據，如時間等）姑且稱作——方向資料（directional statistics/ circular data），把其他資料（中學時就接觸的那些算標準差的資料）稱為——線性資料（data on the line）。

       為了直觀表示方向資料，最簡單的就是把它放在圓上：

       當我們想得到它的一些描述性資料（比如：均值、中位數、標準差等）時，最初的想法可能是在圓上的適當位置把圓斷開，然後用慣常的線性資料方法去求取。這種方法非常依賴於斷點的選擇，為什麼這樣講呢？比如，我們有一個數據集是：1°和359°，在0°處斷開——得到均值是180°，標準差179°；在180°處斷開——得到均值是0°，標準差1°。

         從上面例子中，我們看到這個斷點的選擇對我們描述性資料的影響是多麼大。當然，我認為這種選斷點來處理資料的方法，在一些情況下可能是簡單而有用的——比如上面的例子中，我想大家都會同意斷點在180°處是合理的。

         在Directional Statistics（Mardia&jupp, 2000）一書中，提出了一個適用更為廣泛的方法，來求取方向資料的描述性資料。具體做法是將圓上的點，轉化成平面上的單位向量，再進行後續處理。

資料預處理

         方向可以被視作單位向量x

，或者等同於單位圓上的點。還有另外兩種表示法：角度和單位複數。為單位圓指定初始方向和走向，就可以將單位圓上的點轉化成角度θ或者單位複數z，以下是就是單位向量x的相關表示：

        (參看圖3)

         方向用角度來表示可視作固有方法，因為方向本身就被當作圓上的點；方向用複數來表示可視作一種嵌入式的方法，因為這時方向被當作了平面上特殊的點。在嵌入式的方法中，原本在圓上的資料分佈被認為是集中分佈在平面的單位圓上。

         值得注意的是，方向用角度或者單位複數來表示時，資料的值依賴於初始方向和走向。一般情況下沒有特別選定初始方向和走向，所以當你在處理同一資料集時，若選擇了特殊的初始方向和走向，要注意資料的一致性。即是說，在方向資料領域，資料本身的屬性——如離散性——與座標無關。

方向資料的均值

         假設我們有單位向量，來表示對應角度。那麼的平均方向就是的中心所指的方向。因為笛卡爾座標系中的座標是，因此資料集的中心就是，其中：

因此就是下式的結果：

其中平均值長度是：

值得注意的是時，是不存在的，或者說此種情況下我們沒有定義樣本的均值，當>0時，可這樣求得：

其中‘arctan'是正切函式的反函式，取值範圍是[-π/2, π/2]，注意這裡不等於

角度座標系的問題

       羅盤的角度座標系建立如圖a，在Mardia的書中座標系建立如圖b，下面以分別以x，y指代a、b中的角度值：

在兩座標系中，x和y有如下關係：

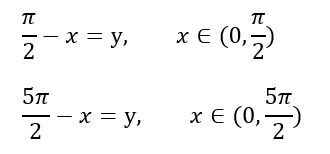
 上面Mardia座標系下求得的，其值的範圍是(-π/2, -3π/2)，所以在求得時候要注意下這個問題。下面是我在python中編寫的求均值的程式：

#!/usr/bin/python
# -*- coding: UTF-8 -*-
'''
@author: liucheng
created on 2018-10-16
Discription: This program is to calculate the discriptive measures --like variance, standard deviation, mean direction and so on-- of directional statistics

'''

import math
# import pandas as pd

# calculate standard deviation of angles
def calc_angles_stddev(data_list):    
    m_sin, m_cos = calc_mean_sin_cos(data_list)

    stddev = math.sqrt(-math.log(m_sin**2 + m_cos**2))#calculate standard deviation
    return stddev

# mean angle calculation in Mardia's coordinates
def calc_angles_mean1(data_list):
    m_sin, m_cos = calc_mean_sin_cos(data_list)

    mean_angle = math.atan(m_sin/m_cos)*(180/math.pi)  #calculate mean angle
    arctan1 = math.atan(m_sin/m_cos)*(180/math.pi)
    if (m_cos >= 0 ):
        mean_angle = mean_angle
    elif (m_cos < 0):
        mean_angle = mean_angle + 180
    if mean_angle < 0 :
        mean_angle = 360 + mean_angle  # 將 (-pi/2, 0)這一段的值轉換成正值
    return mean_angle


# # mean angle calculation in compass coordinates
def calc_angles_mean2(data_list):
    lst = []
    for elem in data_list:  # 座標系轉換，將羅盤座標系的角度值，轉換到Mardia的座標系下
        if elem > 90:
            elem = 450 - elem
        else:
            elem = 90 - elem
        lst.append(elem)
    
    m_sin, m_cos = calc_mean_sin_cos(lst) # 算 sin 和 cos 均值

    mean_angle = math.atan(m_sin/m_cos)*(180/math.pi)  # 計算角度均值，
    arctan2 = math.atan(m_sin/m_cos)*(180/math.pi)

    if (m_cos >= 0 ): # 依據Mardia的方法，均值轉換
        mean_angle = mean_angle
    elif (m_cos < 0):
        mean_angle = mean_angle + 180

    if mean_angle < 0:  # 上面計算得到的均值範圍(-pi/2, 3pi/2)，這裡將負值轉換成正值
        mean_angle = 360 + mean_angle

    if mean_angle < 90:  # 將均值再轉換回風向本身座標系下
        mean_angle = 90 - mean_angle
    else:
        mean_angle = 450 - mean_angle

    return mean_angle

# calculation of mean sine and cosine for a set of angles
def calc_mean_sin_cos(data_list):
    m_sin = 0
    m_cos = 0
    for data_elmt in data_list:
        m_sin += math.sin(math.radians(data_elmt))
        m_cos += math.cos(math.radians(data_elmt))
    m_sin /= len(data_list)  #average of list sin
    m_cos /= len(data_list)

    return m_sin, m_cos


if __name__ == '__main__':
    data_list = [43, 45, 52, 61, 75, 88, 88, 297, 357] # a data set of angles
    a1 = calc_angles_mean1(data_list) # calculate mean angles in Mardia's coordinates
    a2 = calc_angles_mean2(data_list) # calculate mean angles in Compass coordinates

    dev = calc_angles_stddev(data_list)
        
    print('a1 = ', a1, '\na2 = ', a2, '\ndev = ', dev)

舉個例子，以羅盤座標系為例，稱作例1吧：

       現有資料：[43°，45°，52°，61°，75°，88°，88°，297°，357°]，按照以上方法可以得到平均值和平均值長度：

 

方向資料的中位數

       中位數在統計中也很重要，可以更好地幫我們去描述和理解資料。在方向資料中，中位數要滿足兩個條件：1半數的資料點應該在[,+π]中；2大部分的資料點應該更接近而不是+π。

       根據以上兩個條件，我們可以得到例1——[43°，45°，52°，61°，75°，88°，88°，297°，357°]——的中位數是52°，這個值接近他的均值。

方向資料方差

       上面說到方向平均值的長度是：

       因為都是單位向量，因此：

       這個值是很有意義的，它能反映資料的離散性。具體是：若都緊緊聚集在一起，那麼就接近於1；若相互間都分散地很開，那麼就接近於0。我們可以這麼說吧——的變化與方向資料的離散性成反比——越小，資料越分散，反之亦反。

      的取值範圍是[0, 1]，當=1時，說明所有點集中分佈於同一點上，但是當=0時不能說明點在圓上均勻分佈——下圖就是兩個反例。

       關於能反映離散性這一點，參考書目沒有細說，直接給出了這麼個結論，我想稍稍持有點謹慎的人都會生髮出懷疑——真的能反映離散性嗎？這裡給出稍解釋一下，希望能幫助大家理解（之前做了一次展示，但是大家都沒怎麼明白。。）。

       請看下圖：

       從圖7中，可以看到：當點越來越分散的時候，平均值長度變得越來越小，這樣也就證明了我們前面所說的結論。當然，你可能會說這不是一個嚴謹的證明，只不過是幾個例子罷了。這樣說當然沒錯，但這裡我給不出嚴謹的數學證明，參考書上也沒講，舉這個例子只是為了讓大家明白確實有這樣的趨勢。

       值得注意的是當點均勻分佈在單位圓上時，計算得到=（0,0），而前面我們知道，是這樣求得：

       因此這時就不能得到平均角度值了，實際上這個時候也沒有相應地平均值，或者說我們不好定義在這種情況下平均值應該是什麼。

       所以我們可以直接拿這個值來反映資料的離散性，當然，我們可以也可以另V=1-來作為資料的方差，這樣離散性與方差就是正相關的了。

       此外，Batschelet(1981)把“circular variance”(迴圈資料方差）定義為

 

 

 

方向資料的標準差

       用上面介紹的V和來衡量離散性當然可以，至少能夠定性的說明一些問題，比如比較兩組資料離散性的大小，或者一組資料變化之後，相應離散性是如何變化的。

       下面要介紹的是Mardia書中介紹的一個方向資料的標準差，他提出的這個標準差是為了得到一個類似於線性資料那樣的標準差，即是說這個標準差求得的結果對應於角度值，而之前的V和對離散性而言可以認為是一個沒有實際意義的量綱。先說結論，在directional statistics（Mardia&Jupp， 2000）一書中，給出的方向資料的標準差是這樣的：

他又說對於比較小的，該式可變為（這裡Mardia也未說明原因，不知道為什麼，難道他以為讀者很厲害？這些變換都不言自明，一看就明白了？）：

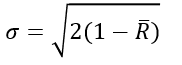
       在CircStat: A MATLAB Toolbox for Circular Statistics（Philipp Berens）一文中，作者說上面兩個式子中後者更常用，因為是有界的[0, ]。

這個標準差得來的原因是假設方向資料在圓上服從正態分佈的，該式得來在directional statistics一書中是這樣介紹的：

1關於Wrapped Distribution（下文簡稱WD，wrapped：包裹、包裝、覆蓋）

定義：給定線性分佈（distribution on the line），我們可以把它包裹（wrap）在單位圓上。即是說，如果x是線上的一個隨機變數，那麼相應地WD的隨機變數是：

若用一組具有單位模長的複數來表示圓，那麼就是：

若x有分佈函式F，那麼的分佈函式是：

特別的，若x有概率密度函式f，那麼相應地的概率密度函式為：

有了以上關於Wrapped Distribution的介紹我們來看看Wrapped Normal Distribution：

2Wrapped Normal Distribution（姑且稱之為：包裹正態分佈）

Mardia在他的書中原話是這樣的：

其中3.5.57即上述（2）式。書裡裡講到這裡就完了，我在書中並未看到關於截圖中3.5.63是怎麼來的。我是這樣想的：

包裹正態分佈就是把正態分佈包裹（wraping ）在圓上得到的，其中：

這個式子怎麼來的呢？我以為是這樣的來的——因為對應線性資料的方差，於是根據上面“包裹”的變換法有：

由（4）進一步得到：

但是（5）相比於（3）等是右邊少了一個2倍的關係，這樣講說不通。

基於此我對Mardia提出的這個標準差有以下看法：

1.Mardia在書中也僅講了擺出來上面那一點，完全沒說清楚，就發明了這麼個標準差出來，因此我認為這個數沒多大參考意義。

2.用到這個數，首先你的資料還得滿足正態分佈，因此其適用範圍有限。

3.既然並沒有多大意義，我認為在衡量離散性時用平均值長度就行了：