紅黑樹解析
目錄
概要
概述:R-B Tree,又稱為“紅黑樹”。本文參考了《演算法導論》中紅黑樹相關知識,加之自己的理解,然後以圖文的形式對紅黑樹進行說明。本文的主要內容包括:紅黑樹的特性,紅黑樹的時間複雜度和它的證明,紅黑樹的左旋、右旋、插入、刪除等操作。
轉載自:http://www.cnblogs.com/skywang12345/p/3245399.html
R-B Tree簡介
R-B Tree,全稱是Red-Black Tree,又稱為“紅黑樹”,它一種特殊的二叉查詢樹。紅黑樹的每個節點上都有儲存位表示節點的顏色,可以是紅(Red)或黑(Black)。
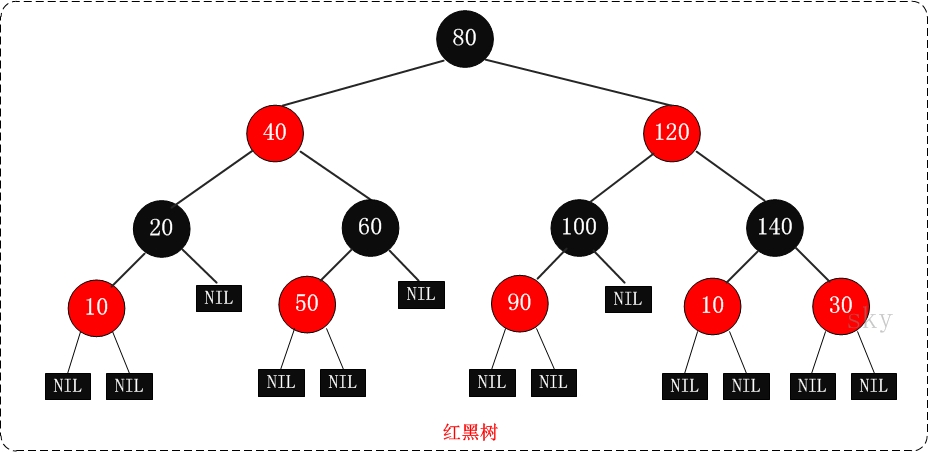
紅黑樹的特性:
(1)每個節點不是黑色就是紅色。
(2)根節點是黑色。
(3)每個葉子節點(NIL)是黑色。 [注意:這裡葉子節點,是指為空(NIL或NULL)的葉子節點!]
(4)如果一個節點是紅色的,則它的子節點必須是黑色的。
(5)從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
注意:
(01) 特性(3)中的葉子節點,是隻為空(NIL或null)的節點。
(02) 特性(5),確保沒有一條路徑會比其他路徑長出倆倍。因而,紅黑樹是相對是接近平衡的二叉樹。
紅黑樹示意圖如下:
紅黑樹的應用
紅黑樹的應用比較廣泛,主要是用它來儲存有序的資料,它的時間複雜度是O(lgn),效率非常之高。
1、在C ++的STL中,地圖和集都是用紅黑樹實現的;
2、著名的Linux的的程序排程完全公平排程程式,用紅黑樹管理程序控制塊,程序的虛擬記憶體區域都儲存在一顆紅黑樹上,每個虛擬地址區域都對應紅黑樹的一個節點,左指標指向相鄰的地址虛擬儲存區域,右指標指向相鄰的高地址虛擬地址空間;
3、IO多路複用的epoll的的的實現採用紅黑樹組織管理的sockfd,以支援快速的增刪改查;
4、Nginx的的的中用紅黑樹管理定時器,因為紅黑樹是有序的,可以很快的得到距離當前最小的定時器;
5、Java中的TreeMap中的實現。
紅黑樹的時間複雜度和相關證明
紅黑樹的時間複雜度為: O(lgn)
下面通過“數學歸納法”對紅黑樹的時間複雜度進行證明。
定理:一棵含有n個節點的紅黑樹的高度至多為2log(n+1).
證明:
"一棵含有n個節點的紅黑樹的高度至多為2log(n+1)" 的逆否命題是 "高度為h的紅黑樹,它的包含的內節點個數至少為 2h/2-1個"。
我們只需要證明逆否命題,即可證明原命題為真;即只需證明 "高度為h的紅黑樹,它的包含的內節點個數至少為 2h/2-1個"。
從某個節點x出發(不包括該節點)到達一個葉節點的任意一條路徑上,黑色節點的個數稱為該節點的黑高度(x's black height),記為bh(x)。關於bh(x)有兩點需要說明:
第1點:根據紅黑樹的"特性(5) ,即從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點"可知,從節點x出發到達的所有的葉節點具有相同數目的黑節點。這也就意味著,bh(x)的值是唯一的!
第2點:根據紅黑色的"特性(4),即如果一個節點是紅色的,則它的子節點必須是黑色的"可知,從節點x出發達到葉節點"所經歷的黑節點數目">= "所經歷的紅節點的數目"。假設x是根節點,則可以得出結論"bh(x) >= h/2"。進而,我們只需證明 "高度為h的紅黑樹,它的包含的黑節點個數至少為 2bh(x)-1個"即可。
到這裡,我們將需要證明的定理已經由
"一棵含有n個節點的紅黑樹的高度至多為2log(n+1)"
轉變成只需要證明
"高度為h的紅黑樹,它的包含的內節點個數至少為 2bh(x)-1個"。
下面通過"數學歸納法"開始論證高度為h的紅黑樹,它的包含的內節點個數至少為 2bh(x)-1個"。
(01) 當樹的高度h=0時,
內節點個數是0,bh(x) 為0,2bh(x)-1 也為 0。顯然,原命題成立。
(02) 當h>0,且樹的高度為 h-1 時,它包含的節點個數至少為 2bh(x)-1-1。這個是根據(01)推斷出來的!
下面,由樹的高度為 h-1 的已知條件推出“樹的高度為 h 時,它所包含的節點樹為 2bh(x)-1”。
當樹的高度為 h 時,
對於節點x(x為根節點),其黑高度為bh(x)。
對於節點x的左右子樹,它們黑高度為 bh(x) 或者 bh(x)-1。
根據(02)的已知條件,我們已知 "x的左右子樹,即高度為 h-1 的節點,它包含的節點至少為 2bh(x)-1-1 個";
所以,節點x所包含的節點至少為 ( 2bh(x)-1-1 ) + ( 2bh(x)-1-1 ) + 1 = 2^bh(x)-1。即節點x所包含的節點至少為 2bh(x)-1。
因此,原命題成立。
由(01)、(02)得出,"高度為h的紅黑樹,它的包含的內節點個數至少為 2^bh(x)-1個"。
因此,“一棵含有n個節點的紅黑樹的高度至多為2log(n+1)”。
紅黑樹的基本操作(一) 左旋和右旋
紅黑樹的基本操作是新增、刪除。在對紅黑樹進行新增或刪除之後,都會用到旋轉方法。為什麼呢?道理很簡單,新增或刪除紅黑樹中的節點之後,紅黑樹就發生了變化,可能不滿足紅黑樹的5條性質,也就不再是一顆紅黑樹了,而是一顆普通的樹。而通過旋轉,可以使這顆樹重新成為紅黑樹。簡單點說,旋轉的目的是讓樹保持紅黑樹的特性。
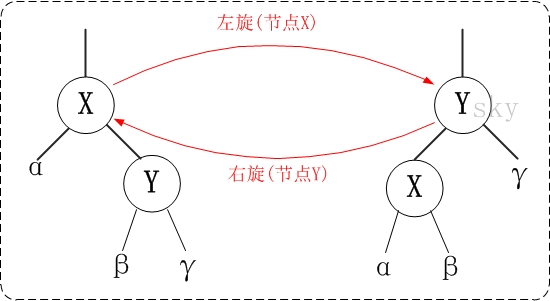
旋轉包括兩種:左旋 和 右旋。下面分別對它們進行介紹。
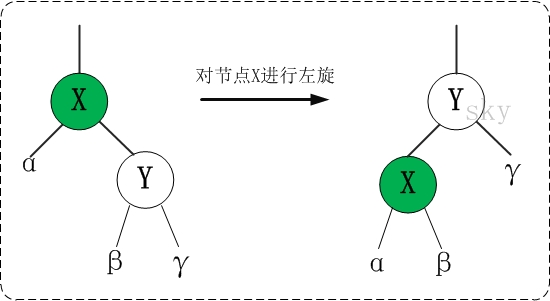
對x進行左旋,意味著"將x變成一個左節點"。
左旋的虛擬碼《演算法導論》:參考上面的示意圖和下面的虛擬碼,理解“紅黑樹T的節點x進行左旋”是如何進行的。
LEFT-ROTATE(T, x)
y ← right[x] // 前提:這裡假設x的右孩子為y。下面開始正式操作
right[x] ← left[y] // 將 “y的左孩子” 設為 “x的右孩子”,即 將β設為x的右孩子
p[left[y]] ← x // 將 “x” 設為 “y的左孩子的父親”,即 將β的父親設為x
p[y] ← p[x] // 將 “x的父親” 設為 “y的父親”
if p[x] = nil[T]
then root[T] ← y // 情況1:如果 “x的父親” 是空節點,則將y設為根節點
else if x = left[p[x]]
then left[p[x]] ← y // 情況2:如果 x是它父節點的左孩子,則將y設為“x的父節點的左孩子”
else right[p[x]] ← y // 情況3:(x是它父節點的右孩子) 將y設為“x的父節點的右孩子”
left[y] ← x // 將 “x” 設為 “y的左孩子”
p[x] ← y // 將 “x的父節點” 設為 “y”
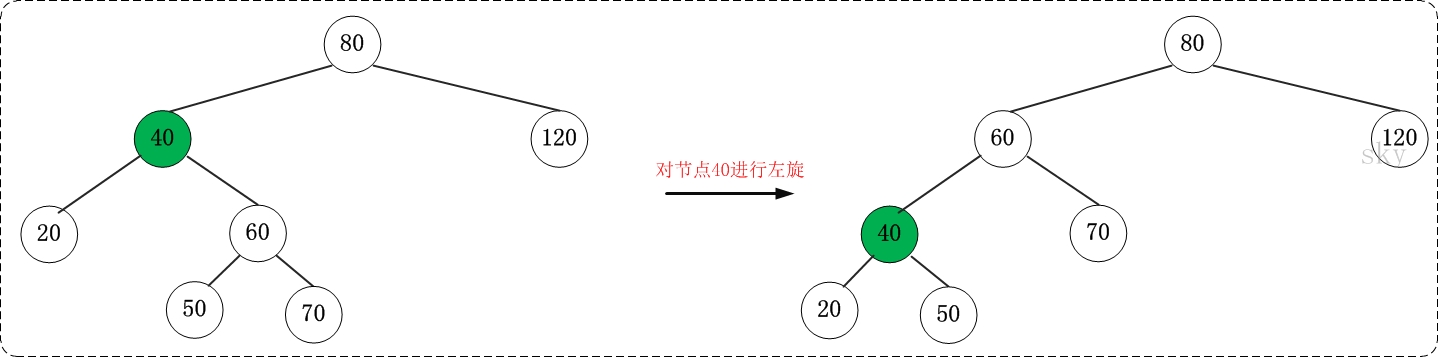
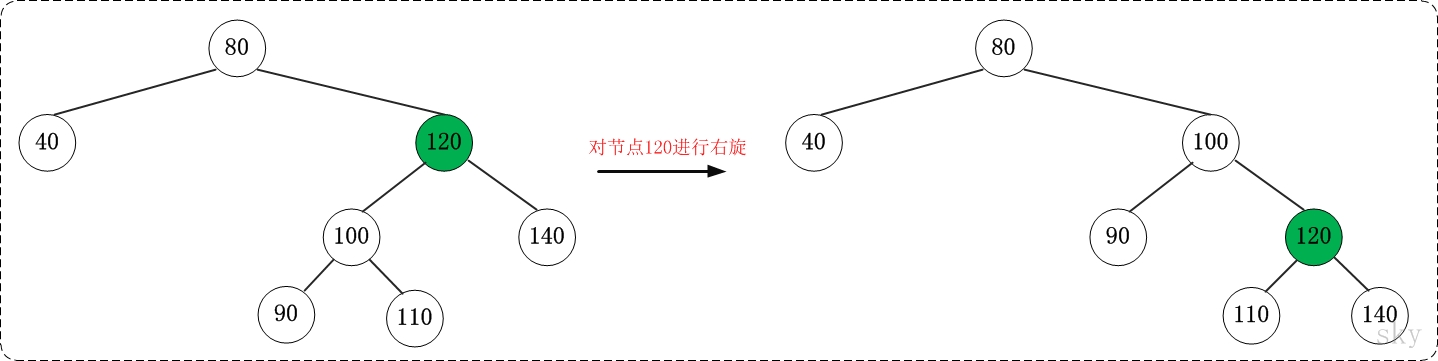
理解左旋之後,看看下面一個更鮮明的例子。你可以先不看右邊的結果,自己嘗試一下。
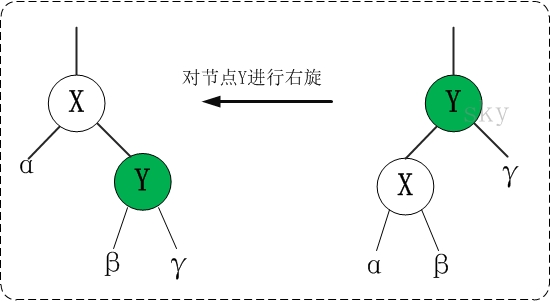
對x進行左旋,意味著"將x變成一個左節點"。
右旋的虛擬碼《演算法導論》:參考上面的示意圖和下面的虛擬碼,理解“紅黑樹T的節點y進行右旋”是如何進行的。
RIGHT-ROTATE(T, y)
x ← left[y] // 前提:這裡假設y的左孩子為x。下面開始正式操作
left[y] ← right[x] // 將 “x的右孩子” 設為 “y的左孩子”,即 將β設為y的左孩子
p[right[x]] ← y // 將 “y” 設為 “x的右孩子的父親”,即 將β的父親設為y
p[x] ← p[y] // 將 “y的父親” 設為 “x的父親”
if p[y] = nil[T]
then root[T] ← x // 情況1:如果 “y的父親” 是空節點,則將x設為根節點
else if y = right[p[y]]
then right[p[y]] ← x // 情況2:如果 y是它父節點的右孩子,則將x設為“y的父節點的左孩子”
else left[p[y]] ← x // 情況3:(y是它父節點的左孩子) 將x設為“y的父節點的左孩子”
right[x] ← y // 將 “y” 設為 “x的右孩子”
p[y] ← x // 將 “y的父節點” 設為 “x”理解右旋之後,看看下面一個更鮮明的例子。你可以先不看右邊的結果,自己嘗試一下。
旋轉總結:
(01) 左旋 和 右旋 是相對的兩個概念,原理類似。理解一個也就理解了另一個。
(02) 下面談談如何區分 左旋 和 右旋。
在實際應用中,若沒有徹底理解 左旋 和 右旋,可能會將它們混淆。下面談談我對如何區分 左旋 和 右旋 的理解。
仔細觀察上面"左旋"和"右旋"的示意圖。我們能清晰的發現,它們是對稱的。無論是左旋還是右旋,被旋轉的樹,在旋轉前是二叉查詢樹,並且旋轉之後仍然是一顆二叉查詢樹。
左旋示例圖(以x為節點進行左旋):
z
x /
/ \ --(左旋)--> x
y z /
y對x進行左旋,意味著,將“x的右孩子”設為“x的父親節點”;即,將 x變成了一個左節點(x成了為z的左孩子)!。 因此,左旋中的“左”,意味著“被旋轉的節點將變成一個左節點”。
右旋示例圖(以x為節點進行右旋):
y
x \
/ \ --(右旋)--> x
y z \
z對x進行右旋,意味著,將“x的左孩子”設為“x的父親節點”;即,將 x變成了一個右節點(x成了為y的右孩子)! 因此,右旋中的“右”,意味著“被旋轉的節點將變成一個右節點”。
紅黑樹的基本操作(二) 新增
將一個節點插入到紅黑樹中,需要執行哪些步驟呢?首先,將紅黑樹當作一顆二叉查詢樹,將節點插入;然後,將節點著色為紅色;最後,通過旋轉和重新著色等方法來修正該樹,使之重新成為一顆紅黑樹。詳細描述如下:
第一步: 將紅黑樹當作一顆二叉查詢樹,將節點插入。
紅黑樹本身就是一顆二叉查詢樹,將節點插入後,該樹仍然是一顆二叉查詢樹。也就意味著,樹的鍵值仍然是有序的。此外,無論是左旋還是右旋,若旋轉之前這棵樹是二叉查詢樹,旋轉之後它一定還是二叉查詢樹。這也就意味著,任何的旋轉和重新著色操作,都不會改變它仍然是一顆二叉查詢樹的事實。
好吧?那接下來,我們就來想方設法的旋轉以及重新著色,使這顆樹重新成為紅黑樹!
第二步:將插入的節點著色為"紅色"。
為什麼著色成紅色,而不是黑色呢?為什麼呢?在回答之前,我們需要重新溫習一下紅黑樹的特性:
(1) 每個節點或者是黑色,或者是紅色。
(2) 根節點是黑色。
(3) 每個葉子節點是黑色。 [注意:這裡葉子節點,是指為空的葉子節點!]
(4) 如果一個節點是紅色的,則它的子節點必須是黑色的。
(5) 從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
將插入的節點著色為紅色,不會違背"特性(5)"!少違背一條特性,就意味著我們需要處理的情況越少。接下來,就要努力的讓這棵樹滿足其它性質即可;滿足了的話,它就又是一顆紅黑樹了。o(∩∩)o...哈哈
第三步: 通過一系列的旋轉或著色等操作,使之重新成為一顆紅黑樹。
第二步中,將插入節點著色為"紅色"之後,不會違背"特性(5)"。那它到底會違背哪些特性呢?
對於"特性(1)",顯然不會違背了。因為我們已經將它塗成紅色了。
對於"特性(2)",顯然也不會違背。在第一步中,我們是將紅黑樹當作二叉查詢樹,然後執行的插入操作。而根據二叉查詢數的特點,插入操作不會改變根節點。所以,根節點仍然是黑色。
對於"特性(3)",顯然不會違背了。這裡的葉子節點是指的空葉子節點,插入非空節點並不會對它們造成影響。
對於"特性(4)",是有可能違背的!
那接下來,想辦法使之"滿足特性(4)",就可以將樹重新構造成紅黑樹了。
下面看看程式碼到底是怎樣實現這三步的。
新增操作的虛擬碼《演算法導論》
RB-INSERT(T, z)
y ← nil[T] // 新建節點“y”,將y設為空節點。
x ← root[T] // 設“紅黑樹T”的根節點為“x”
while x ≠ nil[T] // 找出要插入的節點“z”在二叉樹T中的位置“y”
do y ← x
if key[z] < key[x]
then x ← left[x]
else x ← right[x]
p[z] ← y // 設定 “z的父親” 為 “y”
if y = nil[T]
then root[T] ← z // 情況1:若y是空節點,則將z設為根
else if key[z] < key[y]
then left[y] ← z // 情況2:若“z所包含的值” < “y所包含的值”,則將z設為“y的左孩子”
else right[y] ← z // 情況3:(“z所包含的值” >= “y所包含的值”)將z設為“y的右孩子”
left[z] ← nil[T] // z的左孩子設為空
right[z] ← nil[T] // z的右孩子設為空。至此,已經完成將“節點z插入到二叉樹”中了。
color[z] ← RED // 將z著色為“紅色”
RB-INSERT-FIXUP(T, z) // 通過RB-INSERT-FIXUP對紅黑樹的節點進行顏色修改以及旋轉,讓樹T仍然是一顆紅黑樹結合虛擬碼以及為程式碼上面的說明,先理解RB-INSERT。理解了RB-INSERT之後,我們接著對 RB-INSERT-FIXUP的虛擬碼進行說明。
新增修正操作的虛擬碼《演算法導論》
RB-INSERT-FIXUP(T, z)
while color[p[z]] = RED // 若“當前節點(z)的父節點是紅色”,則進行以下處理。
do if p[z] = left[p[p[z]]] // 若“z的父節點”是“z的祖父節點的左孩子”,則進行以下處理。
then y ← right[p[p[z]]] // 將y設定為“z的叔叔節點(z的祖父節點的右孩子)”
if color[y] = RED // Case 1條件:叔叔是紅色
then color[p[z]] ← BLACK ▹ Case 1 // (01) 將“父節點”設為黑色。
color[y] ← BLACK ▹ Case 1 // (02) 將“叔叔節點”設為黑色。
color[p[p[z]]] ← RED ▹ Case 1 // (03) 將“祖父節點”設為“紅色”。
z ← p[p[z]] ▹ Case 1 // (04) 將“祖父節點”設為“當前節點”(紅色節點)
else if z = right[p[z]] // Case 2條件:叔叔是黑色,且當前節點是右孩子
then z ← p[z] ▹ Case 2 // (01) 將“父節點”作為“新的當前節點”。
LEFT-ROTATE(T, z) ▹ Case 2 // (02) 以“新的當前節點”為支點進行左旋。
color[p[z]] ← BLACK ▹ Case 3 // Case 3條件:叔叔是黑色,且當前節點是左孩子。(01) 將“父節點”設為“黑色”。
color[p[p[z]]] ← RED ▹ Case 3 // (02) 將“祖父節點”設為“紅色”。
RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3 // (03) 以“祖父節點”為支點進行右旋。
else (same as then clause with "right" and "left" exchanged) // 若“z的父節點”是“z的祖父節點的右孩子”,將上面的操作中“right”和“left”交換位置,然後依次執行。
color[root[T]] ← BLACK根據被插入節點的父節點的情況,可以將"當節點z被著色為紅色節點,並插入二叉樹"劃分為三種情況來處理。
① 情況說明:被插入的節點是根節點。
處理方法:直接把此節點塗為黑色。
② 情況說明:被插入的節點的父節點是黑色。
處理方法:什麼也不需要做。節點被插入後,仍然是紅黑樹。
③ 情況說明:被插入的節點的父節點是紅色。
處理方法:那麼,該情況與紅黑樹的“特性(5)”相沖突。這種情況下,被插入節點是一定存在非空祖父節點的;進一步的講,被插入節點也一定存在叔叔節點(即使叔叔節點為空,我們也視之為存在,空節點本身就是黑色節點)。理解這點之後,我們依據"叔叔節點的情況",將這種情況進一步劃分為3種情況(Case)。
| 現象說明 | 處理策略 | |
| Case 1 | 當前節點的父節點是紅色,且當前節點的祖父節點的另一個子節點(叔叔節點)也是紅色。 | (01) 將“父節點”設為黑色。 |
| Case 2 | 當前節點的父節點是紅色,叔叔節點是黑色,且當前節點是其父節點的右孩子 | (01) 將“父節點”作為“新的當前節點”。 |
| Case 3 | 當前節點的父節點是紅色,叔叔節點是黑色,且當前節點是其父節點的左孩子 | (01) 將“父節點”設為“黑色”。 |
上面三種情況(Case)處理問題的核心思路都是:將紅色的節點移到根節點;然後,將根節點設為黑色。下面對它們詳細進行介紹。
1. (Case 1)叔叔是紅色
1.1 現象說明
當前節點(即,被插入節點)的父節點是紅色,且當前節點的祖父節點的另一個子節點(叔叔節點)也是紅色。
1.2 處理策略
(01) 將“父節點”設為黑色。
(02) 將“叔叔節點”設為黑色。
(03) 將“祖父節點”設為“紅色”。
(04) 將“祖父節點”設為“當前節點”(紅色節點);即,之後繼續對“當前節點”進行操作。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
“當前節點”和“父節點”都是紅色,違背“特性(4)”。所以,將“父節點”設定“黑色”以解決這個問題。
但是,將“父節點”由“紅色”變成“黑色”之後,違背了“特性(5)”:因為,包含“父節點”的分支的黑色節點的總數增加了1。 解決這個問題的辦法是:將“祖父節點”由“黑色”變成紅色,同時,將“叔叔節點”由“紅色”變成“黑色”。關於這裡,說明幾點:第一,為什麼“祖父節點”之前是黑色?這個應該很容易想明白,因為在變換操作之前,該樹是紅黑樹,“父節點”是紅色,那麼“祖父節點”一定是黑色。 第二,為什麼將“祖父節點”由“黑色”變成紅色,同時,將“叔叔節點”由“紅色”變成“黑色”;能解決“包含‘父節點’的分支的黑色節點的總數增加了1”的問題。這個道理也很簡單。“包含‘父節點’的分支的黑色節點的總數增加了1” 同時也意味著 “包含‘祖父節點’的分支的黑色節點的總數增加了1”,既然這樣,我們通過將“祖父節點”由“黑色”變成“紅色”以解決“包含‘祖父節點’的分支的黑色節點的總數增加了1”的問題; 但是,這樣處理之後又會引起另一個問題“包含‘叔叔’節點的分支的黑色節點的總數減少了1”,現在我們已知“叔叔節點”是“紅色”,將“叔叔節點”設為“黑色”就能解決這個問題。 所以,將“祖父節點”由“黑色”變成紅色,同時,將“叔叔節點”由“紅色”變成“黑色”;就解決了該問題。
按照上面的步驟處理之後:當前節點、父節點、叔叔節點之間都不會違背紅黑樹特性,但祖父節點卻不一定。若此時,祖父節點是根節點,直接將祖父節點設為“黑色”,那就完全解決這個問題了;若祖父節點不是根節點,那我們需要將“祖父節點”設為“新的當前節點”,接著對“新的當前節點”進行分析。
1.3 示意圖
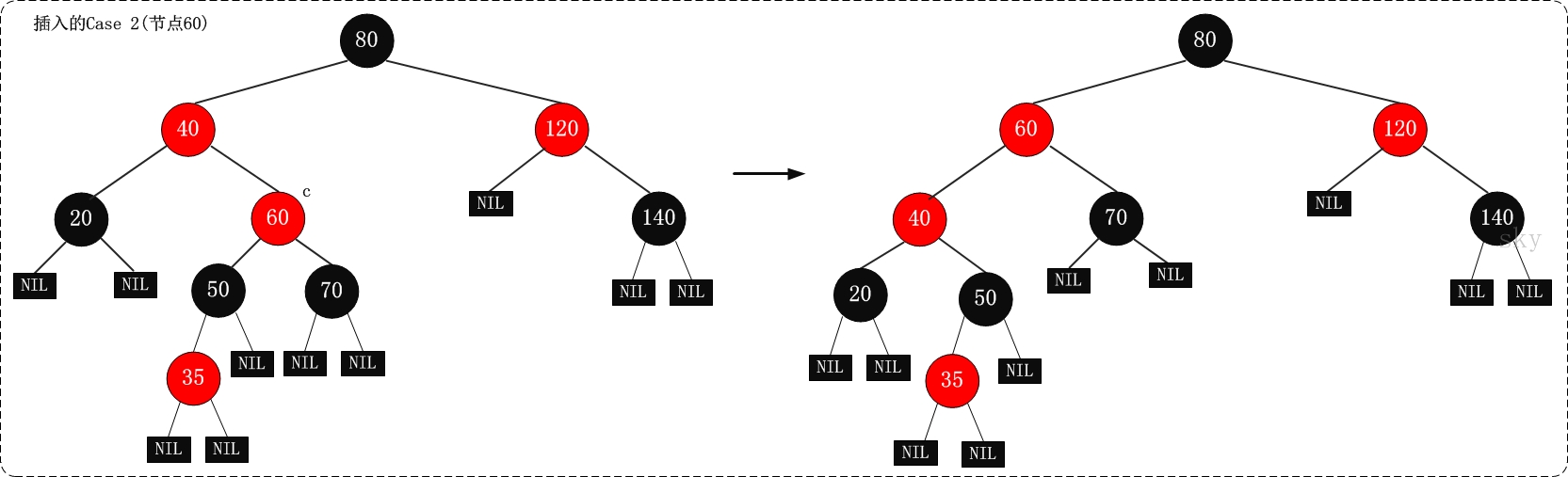
2. (Case 2)叔叔是黑色,且當前節點是右孩子
2.1 現象說明
當前節點(即,被插入節點)的父節點是紅色,叔叔節點是黑色,且當前節點是其父節點的右孩子
2.2 處理策略
(01) 將“父節點”作為“新的當前節點”。
(02) 以“新的當前節點”為支點進行左旋。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
首先,將“父節點”作為“新的當前節點”;接著,以“新的當前節點”為支點進行左旋。 為了便於理解,我們先說明第(02)步,再說明第(01)步;為了便於說明,我們設定“父節點”的代號為F(Father),“當前節點”的代號為S(Son)。
為什麼要“以F為支點進行左旋”呢?根據已知條件可知:S是F的右孩子。而之前我們說過,我們處理紅黑樹的核心思想:將紅色的節點移到根節點;然後,將根節點設為黑色。既然是“將紅色的節點移到根節點”,那就是說要不斷的將破壞紅黑樹特性的紅色節點上移(即向根方向移動)。 而S又是一個右孩子,因此,我們可以通過“左旋”來將S上移!
按照上面的步驟(以F為支點進行左旋)處理之後:若S變成了根節點,那麼直接將其設為“黑色”,就完全解決問題了;若S不是根節點,那我們需要執行步驟(01),即“將F設為‘新的當前節點’”。那為什麼不繼續以S為新的當前節點繼續處理,而需要以F為新的當前節點來進行處理呢?這是因為“左旋”之後,F變成了S的“子節點”,即S變成了F的父節點;而我們處理問題的時候,需要從下至上(由葉到根)方向進行處理;也就是說,必須先解決“孩子”的問題,再解決“父親”的問題;所以,我們執行步驟(01):將“父節點”作為“新的當前節點”。
2.2 示意圖
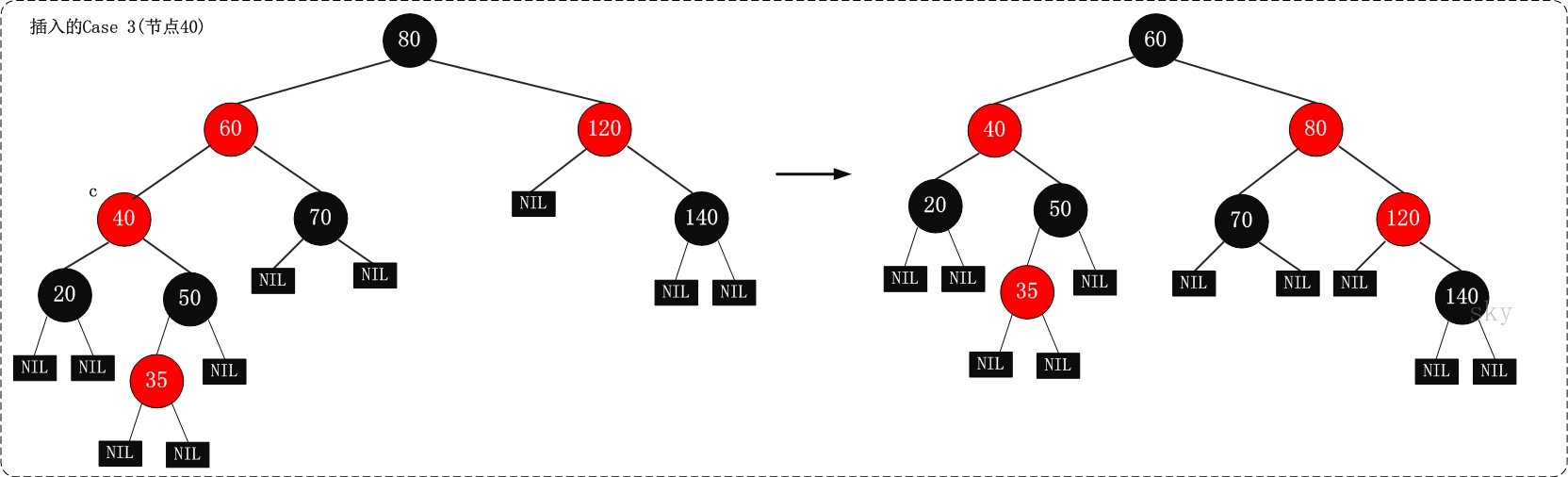
3. (Case 3)叔叔是黑色,且當前節點是左孩子
3.1 現象說明
當前節點(即,被插入節點)的父節點是紅色,叔叔節點是黑色,且當前節點是其父節點的左孩子
3.2 處理策略
(01) 將“父節點”設為“黑色”。
(02) 將“祖父節點”設為“紅色”。
(03) 以“祖父節點”為支點進行右旋。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
為了便於說明,我們設定“當前節點”為S(Original Son),“兄弟節點”為B(Brother),“叔叔節點”為U(Uncle),“父節點”為F(Father),祖父節點為G(Grand-Father)。
S和F都是紅色,違背了紅黑樹的“特性(4)”,我們可以將F由“紅色”變為“黑色”,就解決了“違背‘特性(4)’”的問題;但卻引起了其它問題:違背特性(5),因為將F由紅色改為黑色之後,所有經過F的分支的黑色節點的個數增加了1。那我們如何解決“所有經過F的分支的黑色節點的個數增加了1”的問題呢? 我們可以通過“將G由黑色變成紅色”,同時“以G為支點進行右旋”來解決。
2.3 示意圖
提示:上面的進行Case 3處理之後,再將節點"120"當作當前節點,就變成了Case 2的情況。
紅黑樹的基本操作(三) 刪除
將紅黑樹內的某一個節點刪除。需要執行的操作依次是:首先,將紅黑樹當作一顆二叉查詢樹,將該節點從二叉查詢樹中刪除;然後,通過"旋轉和重新著色"等一系列來修正該樹,使之重新成為一棵紅黑樹。詳細描述如下:
第一步:將紅黑樹當作一顆二叉查詢樹,將節點刪除。
這和"刪除常規二叉查詢樹中刪除節點的方法是一樣的"。分3種情況:
① 被刪除節點沒有兒子,即為葉節點。那麼,直接將該節點刪除就OK了。
② 被刪除節點只有一個兒子。那麼,直接刪除該節點,並用該節點的唯一子節點頂替它的位置。
③ 被刪除節點有兩個兒子。那麼,先找出它的後繼節點;然後把“它的後繼節點的內容”複製給“該節點的內容”;之後,刪除“它的後繼節點”。在這裡,後繼節點相當於替身,在將後繼節點的內容複製給"被刪除節點"之後,再將後繼節點刪除。這樣就巧妙的將問題轉換為"刪除後繼節點"的情況了,下面就考慮後繼節點。 在"被刪除節點"有兩個非空子節點的情況下,它的後繼節點不可能是雙子非空。既然"的後繼節點"不可能雙子都非空,就意味著"該節點的後繼節點"要麼沒有兒子,要麼只有一個兒子。若沒有兒子,則按"情況① "進行處理;若只有一個兒子,則按"情況② "進行處理。
第二步:通過"旋轉和重新著色"等一系列來修正該樹,使之重新成為一棵紅黑樹。
因為"第一步"中刪除節點之後,可能會違背紅黑樹的特性。所以需要通過"旋轉和重新著色"來修正該樹,使之重新成為一棵紅黑樹。
刪除操作的虛擬碼《演算法導論》
RB-DELETE(T, z)
if left[z] = nil[T] or right[z] = nil[T]
then y ← z // 若“z的左孩子” 或 “z的右孩子”為空,則將“z”賦值給 “y”;
else y ← TREE-SUCCESSOR(z) // 否則,將“z的後繼節點”賦值給 “y”。
if left[y] ≠ nil[T]
then x ← left[y] // 若“y的左孩子” 不為空,則將“y的左孩子” 賦值給 “x”;
else x ← right[y] // 否則,“y的右孩子” 賦值給 “x”。
p[x] ← p[y] // 將“y的父節點” 設定為 “x的父節點”
if p[y] = nil[T]
then root[T] ← x // 情況1:若“y的父節點” 為空,則設定“x” 為 “根節點”。
else if y = left[p[y]]
then left[p[y]] ← x // 情況2:若“y是它父節點的左孩子”,則設定“x” 為 “y的父節點的左孩子”
else right[p[y]] ← x // 情況3:若“y是它父節點的右孩子”,則設定“x” 為 “y的父節點的右孩子”
if y ≠ z
then key[z] ← key[y] // 若“y的值” 賦值給 “z”。注意:這裡只拷貝z的值給y,而沒有拷貝z的顏色!!!
copy y's satellite data into z
if color[y] = BLACK
then RB-DELETE-FIXUP(T, x) // 若“y為黑節點”,則呼叫
return y結合虛擬碼以及為程式碼上面的說明,先理解RB-DELETE。理解了RB-DELETE之後,接著對 RB-DELETE-FIXUP的虛擬碼進行說明
RB-DELETE-FIXUP(T, x)
while x ≠ root[T] and color[x] = BLACK
do if x = left[p[x]]
then w ← right[p[x]] // 若 “x”是“它父節點的左孩子”,則設定 “w”為“x的叔叔”(即x為它父節點的右孩子)
if color[w] = RED // Case 1: x是“黑+黑”節點,x的兄弟節點是紅色。(此時x的父節點和x的兄弟節點的子節點都是黑節點)。
then color[w] ← BLACK ▹ Case 1 // (01) 將x的兄弟節點設為“黑色”。
color[p[x]] ← RED ▹ Case 1 // (02) 將x的父節點設為“紅色”。
LEFT-ROTATE(T, p[x]) ▹ Case 1 // (03) 對x的父節點進行左旋。
w ← right[p[x]] ▹ Case 1 // (04) 左旋後,重新設定x的兄弟節點。
if color[left[w]] = BLACK and color[right[w]] = BLACK // Case 2: x是“黑+黑”節點,x的兄弟節點是黑色,x的兄弟節點的兩個孩子都是黑色。
then color[w] ← RED ▹ Case 2 // (01) 將x的兄弟節點設為“紅色”。
x ← p[x] ▹ Case 2 // (02) 設定“x的父節點”為“新的x節點”。
else if color[right[w]] = BLACK // Case 3: x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的左孩子是紅色,右孩子是黑色的。
then color[left[w]] ← BLACK ▹ Case 3 // (01) 將x兄弟節點的左孩子設為“黑色”。
color[w] ← RED ▹ Case 3 // (02) 將x兄弟節點設為“紅色”。
RIGHT-ROTATE(T, w) ▹ Case 3 // (03) 對x的兄弟節點進行右旋。
w ← right[p[x]] ▹ Case 3 // (04) 右旋後,重新設定x的兄弟節點。
color[w] ← color[p[x]] ▹ Case 4 // Case 4: x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的右孩子是紅色的。(01) 將x父節點顏色 賦值給 x的兄弟節點。
color[p[x]] ← BLACK ▹ Case 4 // (02) 將x父節點設為“黑色”。
color[right[w]] ← BLACK ▹ Case 4 // (03) 將x兄弟節點的右子節設為“黑色”。
LEFT-ROTATE(T, p[x]) ▹ Case 4 // (04) 對x的父節點進行左旋。
x ← root[T] ▹ Case 4 // (05) 設定“x”為“根節點”。
else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父節點的右孩子”,將上面的操作中“right”和“left”交換位置,然後依次執行。
color[x] ← BLACK下面對刪除函式進行分析。在分析之前,我們再次溫習一下紅黑樹的幾個特性:
(1) 每個節點或者是黑色,或者是紅色。
(2) 根節點是黑色。
(3) 每個葉子節點是黑色。 [注意:這裡葉子節點,是指為空的葉子節點!]
(4) 如果一個節點是紅色的,則它的子節點必須是黑色的。
(5) 從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
前面我們將"刪除紅黑樹中的節點"大致分為兩步,在第一步中"將紅黑樹當作一顆二叉查詢樹,將節點刪除"後,可能違反"特性(2)、(4)、(5)"三個特性。第二步需要解決上面的三個問題,進而保持紅黑樹的全部特性。
為了便於分析,我們假設"x包含一個額外的黑色"(x原本的顏色還存在),這樣就不會違反"特性(5)"。為什麼呢?
通過RB-DELETE演算法,我們知道:刪除節點y之後,x佔據了原來節點y的位置。 既然刪除y(y是黑色),意味著減少一個黑色節點;那麼,再在該位置上增加一個黑色即可。這樣,當我們假設"x包含一個額外的黑色",就正好彌補了"刪除y所丟失的黑色節點",也就不會違反"特性(5)"。 因此,假設"x包含一個額外的黑色"(x原本的顏色還存在),這樣就不會違反"特性(5)"。
現在,x不僅包含它原本的顏色屬性,x還包含一個額外的黑色。即x的顏色屬性是"紅+黑"或"黑+黑",它違反了"特性(1)"。
現在,我們面臨的問題,由解決"違反了特性(2)、(4)、(5)三個特性"轉換成了"解決違反特性(1)、(2)、(4)三個特性"。RB-DELETE-FIXUP需要做的就是通過演算法恢復紅黑樹的特性(1)、(2)、(4)。RB-DELETE-FIXUP的思想是:將x所包含的額外的黑色不斷沿樹上移(向根方向移動),直到出現下面的姿態:
a) x指向一個"紅+黑"節點。此時,將x設為一個"黑"節點即可。
b) x指向根。此時,將x設為一個"黑"節點即可。
c) 非前面兩種姿態。
將上面的姿態,可以概括為3種情況。
① 情況說明:x是“紅+黑”節點。
處理方法:直接把x設為黑色,結束。此時紅黑樹性質全部恢復。
② 情況說明:x是“黑+黑”節點,且x是根。
處理方法:什麼都不做,結束。此時紅黑樹性質全部恢復。
③ 情況說明:x是“黑+黑”節點,且x不是根。
處理方法:這種情況又可以劃分為4種子情況。這4種子情況如下表所示:
| 現象說明 | 處理策略 | |
| Case 1 | x是"黑+黑"節點,x的兄弟節點是紅色。(此時x的父節點和x的兄弟節點的子節點都是黑節點)。 | (01) 將x的兄弟節點設為“黑色”。 |
| Case 2 | x是“黑+黑”節點,x的兄弟節點是黑色,x的兄弟節點的兩個孩子都是黑色。 | (01) 將x的兄弟節點設為“紅色”。 |
| Case 3 | x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的左孩子是紅色,右孩子是黑色的。 | (01) 將x兄弟節點的左孩子設為“黑色”。 |
| Case 4 | x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的右孩子是紅色的,x的兄弟節點的左孩子任意顏色。 | (01) 將x父節點顏色 賦值給 x的兄弟節點。 |
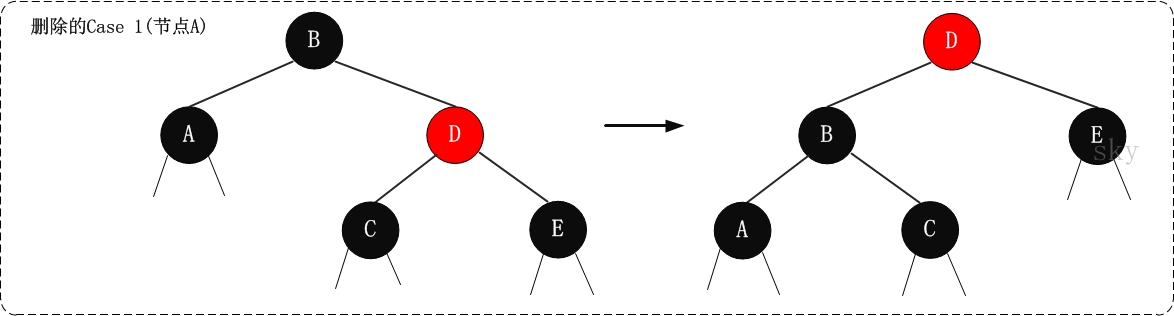
1. (Case 1)x是"黑+黑"節點,x的兄弟節點是紅色
1.1 現象說明
x是"黑+黑"節點,x的兄弟節點是紅色。(此時x的父節點和x的兄弟節點的子節點都是黑節點)。
1.2 處理策略
(01) 將x的兄弟節點設為“黑色”。
(02) 將x的父節點設為“紅色”。
(03) 對x的父節點進行左旋。
(04) 左旋後,重新設定x的兄弟節點。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
這樣做的目的是將“Case 1”轉換為“Case 2”、“Case 3”或“Case 4”,從而進行進一步的處理。對x的父節點進行左旋;左旋後,為了保持紅黑樹特性,就需要在左旋前“將x的兄弟節點設為黑色”,同時“將x的父節點設為紅色”;左旋後,由於x的兄弟節點發生了變化,需要更新x的兄弟節點,從而進行後續處理。
1.3 示意圖
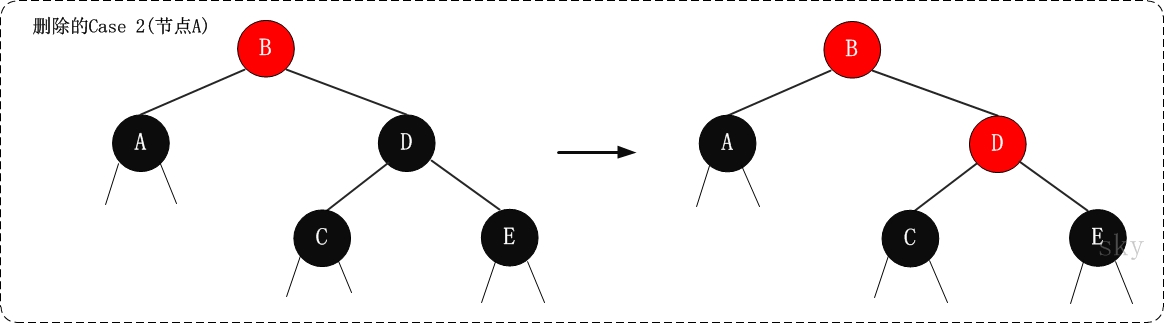
2. (Case 2) x是"黑+黑"節點,x的兄弟節點是黑色,x的兄弟節點的兩個孩子都是黑色
2.1 現象說明
x是“黑+黑”節點,x的兄弟節點是黑色,x的兄弟節點的兩個孩子都是黑色。
2.2 處理策略
(01) 將x的兄弟節點設為“紅色”。
(02) 設定“x的父節點”為“新的x節點”。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
這個情況的處理思想:是將“x中多餘的一個黑色屬性上移(往根方向移動)”。 x是“黑+黑”節點,我們將x由“黑+黑”節點 變成 “黑”節點,多餘的一個“黑”屬性移到x的父節點中,即x的父節點多出了一個黑屬性(若x的父節點原先是“黑”,則此時變成了“黑+黑”;若x的父節點原先時“紅”,則此時變成了“紅+黑”)。 此時,需要注意的是:所有經過x的分支中黑節點個數沒變化;但是,所有經過x的兄弟節點的分支中黑色節點的個數增加了1(因為x的父節點多了一個黑色屬性)!為了解決這個問題,我們需要將“所有經過x的兄弟節點的分支中黑色節點的個數減1”即可,那麼就可以通過“將x的兄弟節點由黑色變成紅色”來實現。
經過上面的步驟(將x的兄弟節點設為紅色),多餘的一個顏色屬性(黑色)已經跑到x的父節點中。我們需要將x的父節點設為“新的x節點”進行處理。若“新的x節點”是“黑+紅”,直接將“新的x節點”設為黑色,即可完全解決該問題;若“新的x節點”是“黑+黑”,則需要對“新的x節點”進行進一步處理。
2.3 示意圖
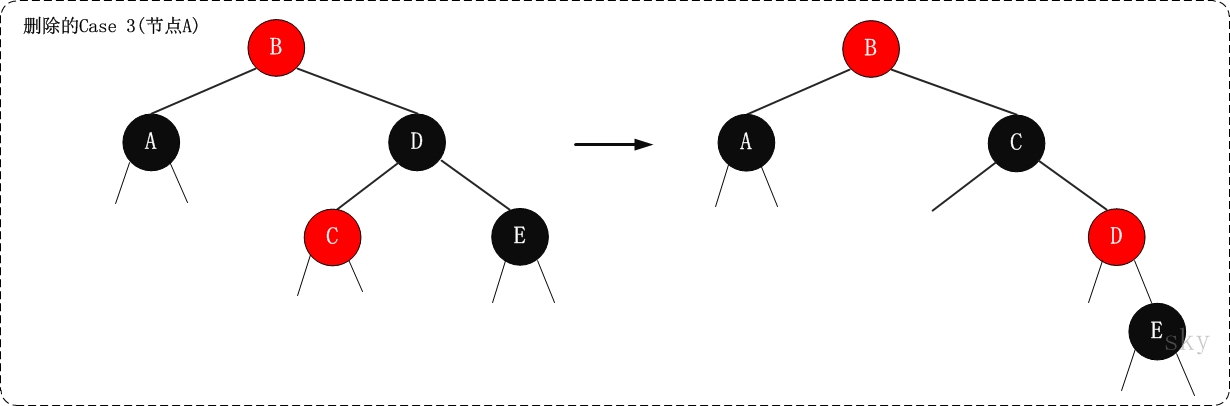
3. (Case 3)x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的左孩子是紅色,右孩子是黑色的
3.1 現象說明
x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的左孩子是紅色,右孩子是黑色的。
3.2 處理策略
(01) 將x兄弟節點的左孩子設為“黑色”。
(02) 將x兄弟節點設為“紅色”。
(03) 對x的兄弟節點進行右旋。
(04) 右旋後,重新設定x的兄弟節點。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
我們處理“Case 3”的目的是為了將“Case 3”進行轉換,轉換成“Case 4”,從而進行進一步的處理。轉換的方式是對x的兄弟節點進行右旋;為了保證右旋後,它仍然是紅黑樹,就需要在右旋前“將x的兄弟節點的左孩子設為黑色”,同時“將x的兄弟節點設為紅色”;右旋後,由於x的兄弟節點發生了變化,需要更新x的兄弟節點,從而進行後續處理。
3.3 示意圖
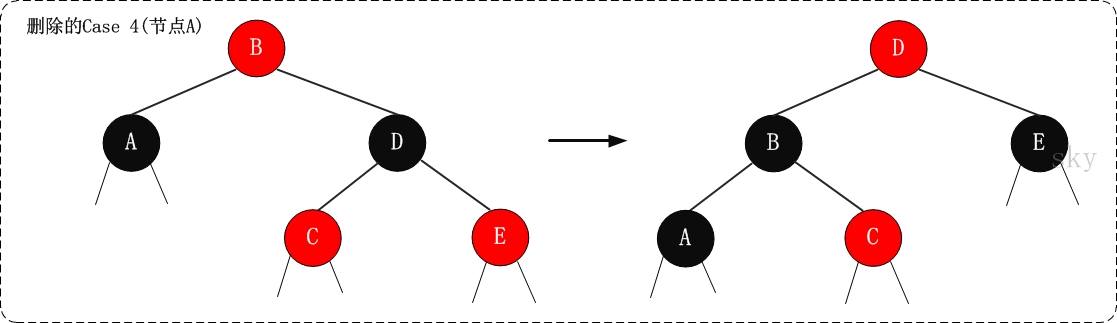
4. (Case 4)x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的右孩子是紅色的,x的兄弟節點的左孩子任意顏色
4.1 現象說明
x是“黑+黑”節點,x的兄弟節點是黑色;x的兄弟節點的右孩子是紅色的,x的兄弟節點的左孩子任意顏色。
4.2 處理策略
(01) 將x父節點顏色 賦值給 x的兄弟節點。
(02) 將x父節點設為“黑色”。
(03) 將x兄弟節點的右子節設為“黑色”。
(04) 對x的父節點進行左旋。
(05) 設定“x”為“根節點”。
下面談談為什麼要這樣處理。(建議理解的時候,通過下面的圖進行對比)
我們處理“Case 4”的目的是:去掉x中額外的黑色,將x變成單獨的黑色。處理的方式是“:進行顏色修改,然後對x的父節點進行左旋。下面,我們來分析是如何實現的。
為了便於說明,我們設定“當前節點”為S(Original Son),“兄弟節點”為B(Brother),“兄弟節點的左孩子”為BLS(Brother's Left Son),“兄弟節點的右孩子”為BRS(Brother's Right Son),“父節點”為F(Father)。
我們要對F進行左旋。但在左旋前,我們需要調換F和B的顏色,並設定BRS為黑色。為什麼需要這裡處理呢?因為左旋後,F和BLS是父子關係,而我們已知BL是紅色,如果F是紅色,則違背了“特性(4)”;為了解決這一問題,我們將“F設定為黑色”。 但是,F設定為黑色之後,為了保證滿足“特性(5)”,即為了保證左旋之後:
第一,“同時經過根節點和S的分支的黑色節點個數不變”。
若滿足“第一”,只需要S丟棄它多餘的顏色即可。因為S的顏色是“黑+黑”,而左旋後“同時經過根節點和S的分支的黑色節點個數”增加了1;現在,只需將S由“黑+黑”變成單獨的“黑”節點,即可滿足“第一”。
第二,“同時經過根節點和BLS的分支的黑色節點數不變”。
若滿足“第二”,只需要將“F的原始顏色”賦值給B即可。之前,我們已經將“F設定為黑色”(即,將B的顏色"黑色",賦值給了F)。至此,我們算是調換了F和B的顏色。
第三,“同時經過根節點和BRS的分支的黑色節點數不變”。
在“第二”已經滿足的情況下,若要滿足“第三”,只需要將BRS設定為“黑色”即可。
經過,上面的處理之後。紅黑樹的特性全部得到的滿足!接著,我們將x設為根節點,就可以跳出while迴圈(參考虛擬碼);即完成了全部處理。
至此,我們就完成了Case 4的處理。理解Case 4的核心,是瞭解如何“去掉當前節點額外的黑色”。
4.3 示意圖
OK!至此,紅黑樹的理論知識差不多講完了。後續再更新紅黑樹的實現程式碼!
紅黑樹和平衡二叉樹區別
1、紅黑樹放棄了追求完全平衡,追求大致平衡,在與平衡二叉樹的時間複雜度相差不大的情況下,保證每次插入最多隻需要三次旋轉就能達到平衡,實現起來也更為簡單。紅黑樹在二叉查詢樹的基礎上增加了著色和相關的性質使得紅黑樹相對平衡,從而保證了紅黑樹的查詢、插入、刪除的時間複雜度最壞為O(log n)。所以紅黑樹適用於搜尋,插入,刪除操作較多的情況。
2、平衡二叉樹追求絕對平衡,條件比較苛刻,實現起來比較麻煩,每次插入新節點之後需要旋轉的次數不能預知。適合用於插入與刪除次數比較少,但查詢多的情況。
參考文獻
1, 《演算法導論》
2, 教你透徹瞭解紅黑樹
更多內容: 資料結構與算法系列 目錄
(01) 紅黑樹(一)之 原理和演算法詳細介紹
(02) 紅黑樹(二)之 C語言的實現
(03) 紅黑樹(三)之 Linux核心中紅黑樹的經典實現
(04) 紅黑樹(四)之 C++的實現
(05) 紅黑樹(五)之 Java的實現
(06) 紅黑樹(六)之 參考資料