1. 什麼是k近鄰演算法？

k最近鄰(k-Nearest Neighbor，kNN)分類演算法是一個比較成熟也是最簡單的機器學習(Machine Learning)演算法之一。該方法的思路是：如果一個樣本在特徵空間中與k個例項最為相似(即特徵空間中最鄰近)，那麼這k個例項中大多數屬於哪個類別，則該樣本也屬於這個類別。

其中，計算樣本與其他例項的相似性一般採用距離衡量法。離得越近越相似，離得越遠越不相似。

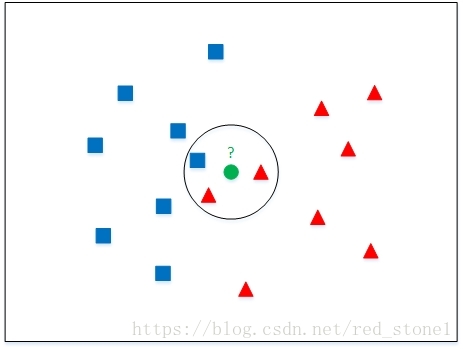
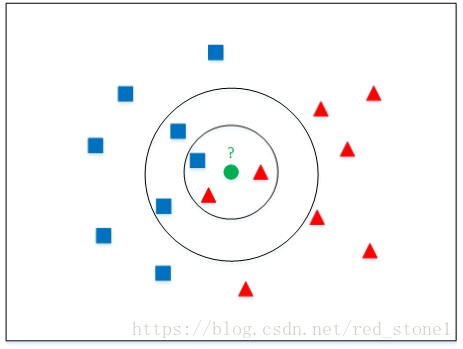
如上圖所示，k=3，距離綠色樣本最近的3個例項中（圓圈內），有兩個是紅色三角形（正類）、一個是藍色正方形（負類）。則該樣本屬於紅色三角形（正類）。

2. k近鄰演算法的本質

我們知道,一般機器學習演算法包括兩個過程：訓練過程和測試過程。訓練過程通過使用機器學習演算法在訓練樣本上迭代訓練，得到較好的機器學習模型；測試過程是使用測試資料來驗證模型的好壞，通過正確率來呈現。kNN演算法的本質是在訓練過程中，它將所有訓練樣本的輸入和輸出標籤(label)都儲存起來。測試過程中，計算測試樣本與每個訓練樣本的距離，選取與測試樣本距離最近的前k個訓練樣本。然後對著k個訓練樣本的label進行投票，票數最多的那一類別即為測試樣本所歸類。

其實，kNN演算法非常簡單，可以說在訓練過程中基本沒有演算法參與，只有儲存訓練樣本。可以說KNN演算法實際上是一種識記類演算法。因此，kNN雖然簡單，但是其明顯包含了以下幾個缺點：

• 整個訓練過程需要將所有的訓練樣本極其輸出label儲存起來，因此，空間成本很大。

• 測試過程中，每個測試樣本都需要與所有的訓練樣本進行比較，執行時間成本很大。

• 採用距離比較的方式，分類準確率不高。

好了，介紹完了kNN演算法的理論知識之後，我相信大家都躍躍欲試了。接下來，我們就來手把手教大家使用Python實現一個kNN分類問題，進入機器學習實戰大門。開始吧～

3. 資料準備

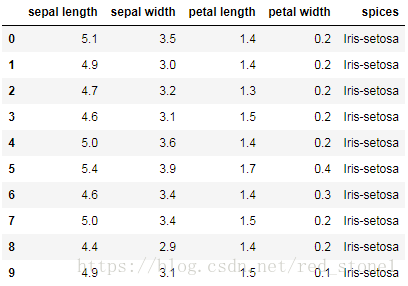
首先，資料集我們選擇經典的鳶尾花卉資料集（Iris）。Iris資料集每個樣本x包含了花萼長度（sepal length）、花萼寬度（sepal width）、花瓣長度（petal length）、花瓣寬度（petal width）四個特徵。樣本標籤y共有三類，分別是Setosa，Versicolor和Virginica。Iris資料集總共包含150個樣本，每個類別由50個樣本，整體構成一個150行5列的二維表，如下圖展示了10個樣本：

如何獲取這些資料呢？很簡單，我們可以使用程式碼，直接從網上下載，下載後的資料集存放在’../data/’目錄下。

import numpy as np
import pandas as pd

data = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)    # 下載iris資料集
#data = pd.read_csv('./data/iris.data.csv', header=None)
data.columns = ['sepal length'
 
, 'sepal width', 'petal length', 'petal width', 'species']    # 特徵及類別名稱

然後，我們將三個類別的資料分別提取出來，setosa、versicolor、virginica分別用0、1、2來表示。

X = data.iloc[0:150, 0:4].values
y = data.iloc[0:150, 4].values
y[y == 'Iris-setosa'] = 0                                 # Iris-setosa 輸出label用0表示
y[y == 'Iris-versicolor'] = 1                             # Iris-versicolor 輸出label用1表示
y[y == 'Iris-virginica'] = 2                              # Iris-virginica 輸出label用2表示
X_setosa, y_setosa = X[0:50], y[0:50]                     # Iris-setosa 4個特徵
X_versicolor, y_versicolor = X[50:100], y[50:100]         # Iris-versicolor 4個特徵
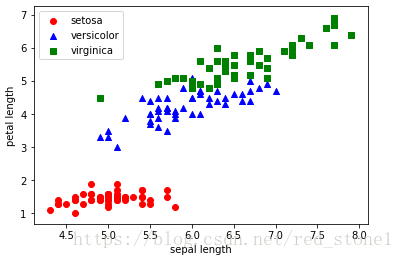
X_virginica, y_virginica = X[100:150], y[100:150]         # Iris-virginica 4個特徵

接下來看一下三種類別不同特徵的空間分佈。為了可視性，我們只選擇sepal length和petal length兩個特徵，在二維平面上作圖。

import matplotlib.pyplot as plt

plt.scatter(X_setosa[:, 0], X_setosa[:, 2], color='red', marker='o', label='setosa')
plt.scatter(X_versicolor[:, 0], X_versicolor[:, 2], color='blue', marker='^', label='versicolor')
plt.scatter(X_virginica[:, 0], X_virginica[:, 2], color='green', marker='s', label='virginica')
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc = 'upper left')
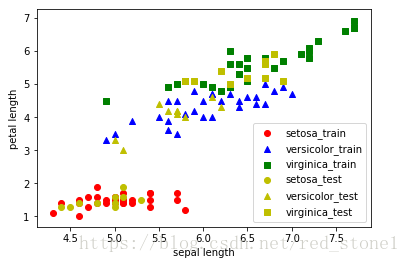
plt.show()

由上圖可見，三個類別之間是有較明顯區別的。

接下來，我們要將每個類別的所有樣本分成訓練樣本（training set）、驗證集(validation set)和測試樣本（test set），各佔所有樣本的比例分別為60%，20%，20%。

# training set
X_setosa_train = X_setosa[:30, :]
y_setosa_train = y_setosa[:30]
X_versicolor_train = X_versicolor[:30, :]
y_versicolor_train = y_versicolor[:30]
X_virginica_train = X_virginica[:30, :]
y_virginica_train = y_virginica[:30]
X_train = np.vstack([X_setosa_train, X_versicolor_train, X_virginica_train])
y_train = np.hstack([y_setosa_train, y_versicolor_train, y_virginica_train])

# validation set
X_setosa_val = X_setosa[30:40, :]
y_setosa_val = y_setosa[30:40]
X_versicolor_val = X_versicolor[30:40, :]
y_versicolor_val = y_versicolor[30:40]
X_virginica_val = X_virginica[30:40, :]
y_virginica_val = y_virginica[30:40]
X_val = np.vstack([X_setosa_val, X_versicolor_val, X_virginica_val])
y_val = np.hstack([y_setosa_val, y_versicolor_val, y_virginica_val])

# test set
X_setosa_test = X_setosa[40:50, :]
y_setosa_test = y_setosa[40:50]
X_versicolor_test = X_versicolor[40:50, :]
y_versicolor_test = y_versicolor[40:50]
X_virginica_test = X_virginica[40:50, :]
y_virginica_test = y_virginica[40:50]
X_test = np.vstack([X_setosa_test, X_versicolor_test, X_virginica_test])
y_test = np.hstack([y_setosa_test, y_versicolor_test, y_virginica_test])

4. kNN訓練函式和預測函式

kNN的訓練過程實際上是一種資料標類、資料儲存的過程，不包含機器學習演算法。首先我們需要定義一個類（class）來實現KNN演算法模組。該類的初始化定義為：

class KNearestNeighbor(object):
   def __init__(self):
       pass

然後，在KNearestNeighbor類中定義訓練函式，訓練函式儲存所有訓練樣本。

def train(self, X, y):
   self.X_train = X
   self.y_train = y

kNN的測試過程是核心部分。其中，有兩點需要注意：

• 衡量距離的方式

• k值的選擇

kNN距離衡量一般有兩種方式：L1距離和L2距離。

L1距離的計算公式為：

其中，I1和I2分別表示兩個樣本，p表示特徵維度。

L2距離的計算公式為：

一般來說，L1距離和L2距離都比較常用。需要注意的是，如果兩個樣本距離越大，那麼使用L2會繼續擴大距離，即對距離大的情況懲罰性越大。反過來說，如果兩個樣本距離較小，那麼使用L2會縮小距離，減小懲罰。也就是說，如果想要放大兩個樣本之間的不同，使用L2距離會更好一些。這裡，我們使用最常用的L2距離。

kNN中的k值選擇至關重要，不同的k值也許能歸屬到不同的類別中，例如在下圖中，k=3，則判定綠色例項屬於紅色三角形類別。

但是，如果令k=5，如下圖所示，則會判定綠色例項屬於藍色正方形類別。

一般來說，k值太小會使模型過於複雜，造成過擬合（overfitting）；k值太大會使模型分類模糊，造成欠擬合(underfitting)。實際應用中，我們可以選擇不同的k值，通過驗證來決定K值大小。程式碼中，我們將k設定為可調引數。

在KNearestNeighbor類中定義預測函式：

def predict(self, X, k=1)
   # 計算L2距離
   num_test = X.shape[0]
   num_train = self.X_train.shape[0]
   dists = np.zeros((num_test, num_train))    # 初始化距離函式
   # because(X - X_train)*(X - X_train) = -2X*X_train + X*X + X_train*X_train, so
   d1 = -2 * np.dot(X, self.X_train.T)    # shape (num_test, num_train)
   d2 = np.sum(np.square(X), axis=1, keepdims=True)    # shape (num_test, 1)
   d3 = np.sum(np.square(self.X_train), axis=1)    # shape (1, num_train)
   dist = np.sqrt(d1 + d2 + d3)
   # 根據K值，選擇最可能屬於的類別
   y_pred = np.zeros(num_test)
   for i in range(num_test):
       dist_k_min = np.argsort(dist[i])[:k]    # 最近鄰k個例項位置
       y_kclose = self.y_train[dist_k_min]     # 最近鄰k個例項對應的標籤
       y_pred[i] = np.argmax(np.bincount(y_kclose))    # 找出k個標籤中從屬類別最多的作為預測類別

   return y_pred

KNearestNeighbor類的完整定義程式碼如下：

class KNearestNeighbor(object):
   def __init__(self):
       pass

   # 訓練函式
   def train(self, X, y):
       self.X_train = X
       self.y_train = y

   # 預測函式
   def predict(self, X, k=1):
       # 計算L2距離
       num_test = X.shape[0]
       num_train = self.X_train.shape[0]
       dists = np.zeros((num_test, num_train))    # 初始化距離函式
       # because(X - X_train)*(X - X_train) = -2X*X_train + X*X + X_train*X_train, so
       d1 = -2 * np.dot(X, self.X_train.T)    # shape (num_test, num_train)
       d2 = np.sum(np.square(X), axis=1, keepdims=True)    # shape (num_test, 1)
       d3 = np.sum(np.square(self.X_train), axis=1)    # shape (1, num_train)
       dist = np.sqrt(d1 + d2 + d3)
       # 根據K值，選擇最可能屬於的類別
       y_pred = np.zeros(num_test)
       for i in range(num_test):
           dist_k_min = np.argsort(dist[i])[:k]    # 最近鄰k個例項位置
           y_kclose = self.y_train[dist_k_min]     # 最近鄰k個例項對應的標籤
           y_pred[i] = np.argmax(np.bincount(y_kclose.tolist()))    # 找出k個標籤中從屬類別最多的作為預測類別

       return y_pred

5. 訓練和預測

首先，建立一個KnearestNeighbor例項物件。

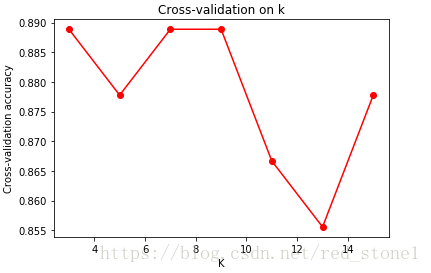
然後，在驗證集上進行k-fold交叉驗證。選擇不同的k值，根據驗證結果，選擇最佳的k值。

可見，k值取3的時候，驗證集的準確率最高。此例中，由於總體樣本資料量不夠多，所以驗證結果並不明顯。但是使用k-fold交叉驗證來選擇最佳k值是最常用的方法之一。

選擇完合適的k值之後，就可以對測試集進行預測分析了。

KNN.train(X_train, y_train)
y_pred = KNN.predict(X_test, k=6)
accuracy = np.mean(y_pred == y_test)
print('測試集預測準確率：%f' % accuracy)

測試集預測準確率：1.000000

最終結果顯示，測試集預測準確率為100%。

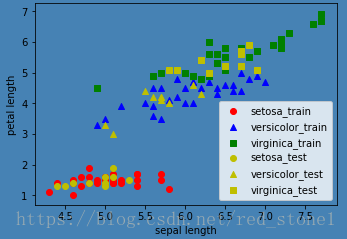
最後，我們把預測結果繪圖表示。仍然只選擇sepal length和petal length兩個特徵，在二維平面上作圖。

# 訓練集
plt.scatter(X_setosa_train[:, 0], X_setosa_train[:, 2], color='red', marker='o', label='setosa_train')
plt.scatter(X_versicolor_train[:, 0], X_versicolor_train[:, 2], color='blue', marker='^', label='versicolor_train')
plt.scatter(X_virginica_train[:, 0], X_virginica_train[:, 2], color='green', marker='s', label='virginica_train')
# 測試集
plt.scatter(X_setosa_test[:, 0], X_setosa_test[:, 2], color='y', marker='o', label='setosa_test')
plt.scatter(X_versicolor_test[:, 0], X_versicolor_test[:, 2], color='y', marker='^', label='versicolor_test')
plt.scatter(X_virginica_test[:, 0], X_virginica_test[:, 2], color='y', marker='s', label='virginica_test')

plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc = 4)
plt.show()

6. k近鄰演算法總結

k近鄰演算法是一種最簡單最直觀的分類演算法。它的訓練過程保留了所有樣本的所有特徵，把所有資訊都記下來，沒有經過處理和提取。而其它機器學習演算法包括神經網路則是在訓練過程中提取最重要、最有代表性的特徵。在這一點上，kNN演算法還非常不夠“智慧”。但是，kNN演算法作為機器學習的基礎演算法，還是值得我們瞭解一下的。

本文的完整原始碼已經放在了GitHub上，請點選「閱讀原文」獲取！

閱讀原文