買賣股票的最佳時機IV

給定一個數組，它的第 i 個元素是一支給定的股票在第 i 天的價格。

設計一個演算法來計算你所能獲取的最大利潤。你最多可以完成 k 筆交易。

注意: 你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

示例 1:

輸入: [2,4,1], k = 2

輸出: 2

解釋: 在第 1 天 (股票價格 = 2) 的時候買入，在第 2 天 (股票價格 = 4) 的時候賣出，這筆交易所能獲得利潤 = 4-2 = 2 。

示例 2:

輸入: [3,2,6,5,0,3], k = 2

輸出: 7

解釋: 在第 2 天 (股票價格 = 2) 的時候買入，在第 3 天 (股票價格 = 6) 的時候賣出, 這筆交易所能獲得利潤 = 6-2 = 4 。

  隨後，在第 5 天 (股票價格 = 0) 的時候買入，在第 6 天 (股票價格 = 3) 的時候賣出, 這筆交易所能獲得利潤 = 3-0 = 3 。

思路：定義兩個二維變數，

last[j][i]，表示恰好在第j日完成第i次交易的最大收益。

total[j][i]，表示在第j日之前（含）完成i次交易的最大收益。

那麼如何遞迴或者遞推計算兩個變數的值呢？我們先考慮total變數，第j日之前完成i次交易，可以分為兩種情況，第一種情況是最後一日不作任何交易，第二種是最後一日完成第i次交易，則total[j][i] = max(total[j-1][i], last[j][i])，這個比較容易理解。如何計算last呢？我們可以按照倒數第二日的交易情況進行分類，分為倒數第二日完成第i次交易，以及倒數第二日不做任何交易。對於前者，我們可以觀察如果倒數第二日的第i次交易推遲到第i日的獲利情況；對於後者，我們可以觀察倒數第二日買入，最後一日（第j日）賣出的情況，即：last[j][i] = max(0, last[j-1][i] + prices[j] - prices[j-1], total[j-1][i-1] + prices[j] - prices[j-1])。為什麼會有0呢？因為我們的交易至少不能虧錢，如果一定要有交易的話，我們當天買入、當天賣出，至少是可以不虧的。但會不會有其他情況呢？例如最後一次交易有沒有可能是倒數第三天買入，最後一天賣出？分析下面六種情況，可以知道公式是正確的。

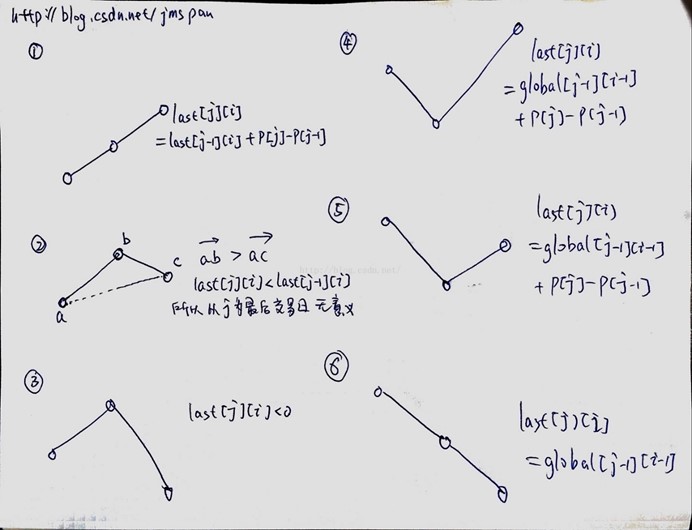
資料流演示：

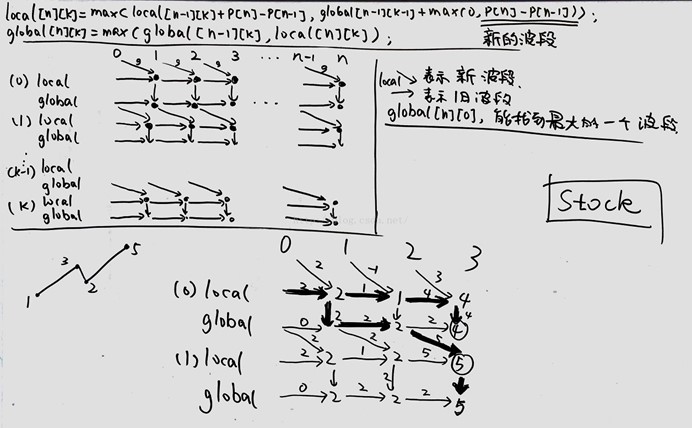
 1 public class Solution {
 2     private int max(int[] prices) {
 3         int max = 0;
 4         for(int i=1; i<prices.length; i++) {
 5             max += Math.max(0, prices[i] - prices[i-1]);
 6         }
 7         return max;
 8     }
 9     public int maxProfit(int
 
 k, int[] prices) {
10         if (prices == null || prices.length < 2) return 0;
11         int n = prices.length;
12         if (k >= n/2) return max(prices);
13         int[][] last = new int[n][k+1];
14         int[][] total = new int[n][k+1];
15         for(int t = 1; t <= k; t ++) {
16             for(int d = 1; d < n; d ++) {
17                 last[d][t] = Math.max(last[d-1][t] + prices[d] - prices[d-1], total[d-1][t-1] + Math.max(0, prices[d] - prices[d-1]));
18                 total[d][t] = Math.max(total[d-1][t], last[d][t]);
19             }
20         }
21         return total[n-1][k];
22     }
23 }