天際線問題

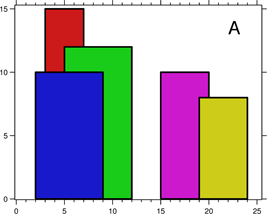
城市的天際線是從遠處觀看該城市中所有建築物形成的輪廓的外部輪廓。現在，假設您獲得了城市風光照片（圖A）上顯示的所有建築物的位置和高度，請編寫一個程式以輸出由這些建築物形成的天際線（圖B）。

每個建築物的幾何資訊用三元組 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分別是第 i 座建築物左右邊緣的 x 座標，Hi 是其高度。可以保證 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假設所有建築物都是在絕對平坦且高度為 0 的表面上的完美矩形。

例如，圖A中所有建築物的尺寸記錄為：[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。

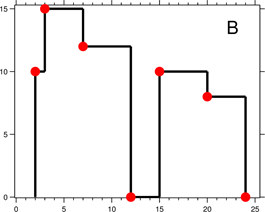
輸出是以 [ [x1,y1], [x2, y2], [x3, y3], ... ] 格式的"關鍵點"（圖B中的紅點）的列表，它們唯一地定義了天際線。關鍵點是水平線段的左端點。請注意，最右側建築物的最後一個關鍵點僅用於標記天際線的終點，並始終為零高度。此外，任何兩個相鄰建築物之間的地面都應被視為天際線輪廓的一部分。

例如，圖B中的天際線應該表示為：[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。

說明:

• 任何輸入列表中的建築物數量保證在 [0, 10000] 範圍內。
• 輸入列表已經按升序排列在左邊的 x 位置 Li 。
• 輸出列表必須按 x 位排序。
• 輸出天際線中不得有連續的相同高度的水平線。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正確的答案；三條高度為 5 的線應該在最終輸出中合併為一個：[...[2 3], [4 5], [12 7], ...]

思路

如果按照一個矩形一個矩形來處理將會非常麻煩，我們可以把這些矩形拆成兩個點，一個左上頂點，一個右上頂點。將所有頂點按照橫座標排序後，我們開始遍歷這些點。遍歷時，通過一個堆來得知當前圖形的最高位置。堆頂是所有頂點中最高的點，只要這個點沒被移出堆，說明這個最高的矩形還沒結束。對於左頂點，我們將其加入堆中。對於右頂點，我們找出堆中其相應的左頂點，然後移出這個左頂點，同時也意味這這個矩形的結束。具體程式碼中，為了在排序後的頂點列表中區分左右頂點，左頂點的值是正數，而右頂點值則存的是負數。

注意

• 堆中先加入一個零點高度，幫助我們在只有最矮的建築物時選擇最低值

複雜度

時間 O(NlogN) 空間 O(N)

 1 public class Solution {
 2     public List<int[]> getSkyline(int[][] buildings) {
 3         List<int[]> result = new ArrayList<>();
 4         List<int[]> height = new ArrayList<>();
 5         // 拆解矩形，構建頂點的列表
 6         for(int[] b:buildings) {
 7             // 左頂點存為負數
 8             height.add(new int[]{b[0], -b[2]});
 9             // 右頂點存為正數
10             height.add(new int[]{b[1], b[2]});
11         }
12         // 根據橫座標對列表排序，相同橫座標的點縱座標小的排在前面
13         Collections.sort(height, new Comparator<int[]>(){
14             public int compare(int[] a, int[] b){
15                 if(a[0] != b[0]){
16                     return a[0] - b[0];
17                 } else {
18                     return a[1] - b[1];
19                 }
20             }
21         });
22         // 構建堆，按照縱座標來判斷大小
23         Queue<Integer> pq = new PriorityQueue<Integer>(11, new Comparator<Integer>(){
24             public int compare(Integer i1, Integer i2){
25                 return i2 - i1;
26             }
27         });
28         // 將地平線值9先加入堆中
29         pq.offer(0);
30         // prev用於記錄上次keypoint的高度
31         int prev = 0;
32         for(int[] h:height) {
33             // 將左頂點加入堆中
34             if(h[1] < 0) {
35                 pq.offer(-h[1]);
36             } else {
37                 // 將右頂點對應的左頂點移去
38                 pq.remove(h[1]);
39             }
40             int cur = pq.peek();
41             // 如果堆的新頂部和上個keypoint高度不一樣，則加入一個新的keypoint
42             if(prev != cur) {
43                 result.add(new int[]{h[0], cur});
44                 prev = cur;
45             }
46         }
47         return result;
48     }
49 }