梯度下降法作為機器學習中較常使用的優化演算法，其有著三種不同的形式：批量梯度下降（Batch Gradient Descent）、隨機梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。其中小批量梯度下降法也常用在深度學習中進行模型的訓練。接下來，我們將對這三種不同的梯度下降法進行理解。
  為了便於理解，這裡我們將使用只含有一個特徵的線性迴歸來展開。此時線性迴歸的假設函式為：
$h_{\theta} (x^{(i)})=\theta_1 x^{(i)}+\theta_0$

  其中$i=1,2,...,m$ 表示樣本數。
  對應的目標函式（代價函式）即為：
  $J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2$
  下圖為 $J(\theta_0,\theta_1)$與引數$\theta_0,\theta_1$

的關係的圖：
  

 

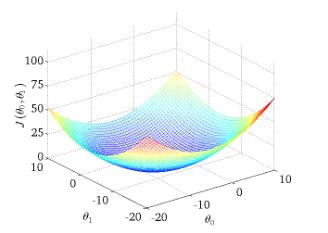
1、批量梯度下降（Batch Gradient Descent，BGD）

  批量梯度下降法是最原始的形式，它是指在每一次迭代時使用所有樣本來進行梯度的更新。從數學上理解如下：
  （1）對目標函式求偏導：
  $\frac{\Delta J(\theta_0,\theta_1)}{\Delta \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$

m1​i=1∑m​(hθ​(x(i))−y(i))xj(i)​
    其中$i=1,2,...,m$表示樣本數，$j=0,1$ 表示特徵數，這裡我們使用了偏置項$x_0^{(i)} = 1$。
  （2）每次迭代對引數進行更新：
  $\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$
   注意這裡更新時存在一個求和函式，即為對所有樣本進行計算處理，可與下文SGD法進行比較。
   虛擬碼形式為：
    repeat
    {
       $\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}(for\ j =0,1)$
    }
    優點：
    （1）一次迭代是對所有樣本進行計算，此時利用矩陣進行操作，實現了並行。
    （2）由全資料集確定的方向能夠更好地代表樣本總體，從而更準確地朝向極值所在的方向。當目標函式為凸函式時，BGD一定能夠得到全域性最優。
    缺點：
    （1）當樣本數目 m 很大時，每迭代一步都需要對所有樣本計算，訓練過程會很慢。
    從迭代的次數上來看，BGD迭代的次數相對較少。其迭代的收斂曲線示意圖可以表示如下：
  

2、隨機梯度下降（Stochastic Gradient Descent，SGD）

  隨機梯度下降法不同於批量梯度下降，隨機梯度下降是每次迭代使用一個樣本來對引數進行更新。使得訓練速度加快。
  對於一個樣本的目標函式為：
$J^{(i)}(\theta_0,\theta_1) = \frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2$
   (1）對目標函式求偏導：
$\frac{\Delta J^{(i)}(\theta_0,\theta_1)}{\theta_j} = (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j$
   (2)引數更新
$\theta_j := \theta_j - \alpha (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j$

    注意，這裡不再有求和符號
    虛擬碼形式為：
    repeat
    {
      for i=1,…,m
      {
         $\theta_j := \theta_j -\alpha (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}(for\ j =0,1)$
      }
    }

  優點：
  （1）由於不是在全部訓練資料上的損失函式，而是在每輪迭代中，隨機優化某一條訓練資料上的損失函式，這樣每一輪引數的更新速度大大加快。
  缺點：
  （1）準確度下降。由於即使在目標函式為強凸函式的情況下，SGD仍舊無法做到線性收斂。
  （2）可能會收斂到區域性最優，由於單個樣本並不能代表全體樣本的趨勢。
  （3）不易於並行實現。

  解釋一下為什麼SGD收斂速度比BGD要快：
  答：這裡我們假設有30W個樣本，對於BGD而言，每次迭代需要計算30W個樣本才能對引數進行一次更新，需要求得最小值可能需要多次迭代（假設這裡是10）；而對於SGD，每次更新引數只需要一個樣本，因此若使用這30W個樣本進行引數更新，則引數會被更新（迭代）30W次，而這期間，SGD就能保證能夠收斂到一個合適的最小值上了。也就是說，在收斂時，BGD計算了 $10×30W$ 次，而SGD只計算了 $1×30W$次。
  從迭代的次數上來看，SGD迭代的次數較多，在解空間的搜尋過程看起來很盲目。其迭代的收斂曲線示意圖可以表示如下：

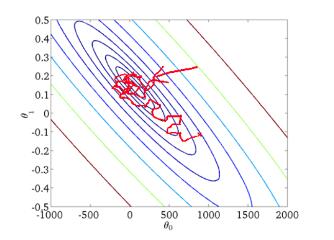
3、小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

  小批量梯度下降，是對批量梯度下降以及隨機梯度下降的一個折中辦法。其思想是：每次迭代 使用 ** batch_size** 個樣本來對引數進行更新。
  這裡我們假設 $batchsize=10$ ，樣本數 $m=1000$ 。
  虛擬碼形式為：
  repeat
  {
    for i=1,11,21,31,…,991
    {
       $\theta_j := \theta_j - \alpha \frac{1}{10} \sum_{k=i}^{(i+9)}(h_{\theta}(x^{(k)})-y^{(k)})x_j^{(k)}(for\ j =0,1)$