繼續補以前拉下的債~~~

一、相關性指標的研究意義
1.1相關係數（Correlation coefficient）：

相關係數是變數間關聯程度的最基本測度之一

1.2相關分析（Correlation analysis）

是研究現象之間是否存在某種依存關係，並對具體有依存關係的現象探討其相關方向以及相關程度，是研究隨機變數之間的相關關係的一種統計方法。

二、相關係數的基本特徵
2.1方向：
    正相關（positive correlation）：兩個變數變化方向相同

    負相關（negative correlation）：兩個變數變化方向相反

2.2量級（magnitude）：

低度相關：0≤| r | ≤ 0.3

    高度相關：0.8≤| r | ≤ 1

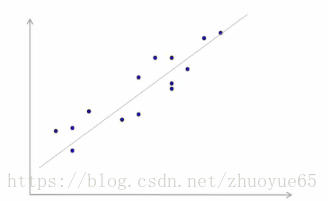
散點分部在一條直線周圍==>變數存線上性相關關係。

三、相關係數的計算

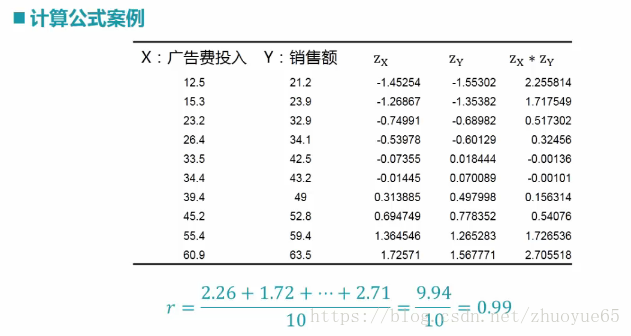
Zx = （每個變數中的值 - 該變數的均值）  除以（標準差）

3.2案例實戰：

四、程式碼案例：
4.1numpy案例：

import numpy

X = [
    12.5, 15.3, 23.2, 26.4, 33.5, 
    34.4, 39.4, 45.2, 55.4, 60.9
]
Y = [
    21.2, 23.9, 32.9, 34.1, 42.5, 
    43.2, 49.0, 52.8, 59.4, 63.5
]

#均值
XMean = numpy.mean(X);
YMean = numpy.mean(Y);

#標準差
XSD = numpy.std(X);
YSD = numpy.std(Y);

#z分數
ZX = (X-XMean)/XSD;
ZY = (Y-YMean)/YSD;

#相關係數
r = numpy.sum(ZX*ZY)/(len(X));

#直接呼叫Python的內建的相關係數的計算方法
numpy.corrcoef(X, Y)  
 

4.2Pandas案例

import pandas;

X = [
    12.5, 15.3, 23.2, 26.4, 33.5, 
    34.4, 39.4, 45.2, 55.4, 60.9
]
Y = [
    21.2, 23.9, 32.9, 34.1, 42.5, 
    43.2, 49.0, 52.8, 59.4, 63.5
]

data = pandas.DataFrame({
    'X': X, 
    'Y': Y
})
data.corr()

？檢視安斯庫姆四重奏