2. 程式人生 > >常微分方程和偏微分方程

常微分方程和偏微分方程

阿新 • • 發佈：2019-01-01

常微分方程

未知函式是隻有一個自變數的方程
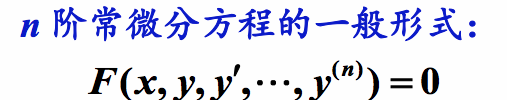
在這裡插入圖片描述
在這裡插入圖片描述
落體運動
是一個一階的常微分方程
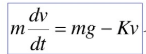
在這裡插入圖片描述
阻尼振動
是一個二階的常微分方程
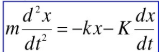
在這裡插入圖片描述

偏微分方程

  • 拉普拉斯方程（調和方程）
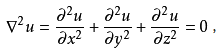
    在這裡插入圖片描述
    拉普拉斯方程是一個二階的偏微分方程。滿足拉普拉斯方程的解被稱為調和函式。該方恆存在於電磁學，熱力學，表面張力，引力學等多個領域。
    如果等號右邊不是0，則該方程稱為柏鬆方程
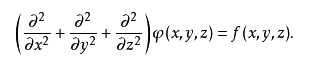
    在這裡插入圖片描述
    引力場：
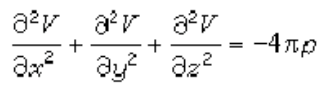
    在這裡插入圖片描述
    V為引力勢。ρ為該點的密度。
    靜電場：
    在這裡插入圖片描述
    ρ為自由電荷的密度。

  • 聲場的波動方程

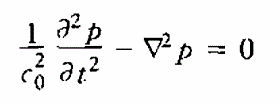
在這裡插入圖片描述

  • 電磁場的波動方程
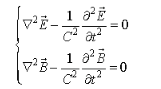
    在這裡插入圖片描述

相關推薦

常微分方程和偏微分方程

常微分方程 未知函式是隻有一個自變數的方程 落體運動 是一個一階的常微分方程 阻尼振動 是一個二階的常微分方程 偏微分方程 拉普拉斯方程（調和方程） 拉普拉斯方程是一個二階的偏微分方程。滿足拉普拉斯方程的解被稱為調和函式。該方恆存在於電磁學，熱力學，表面張力，

數學筆記12——常微分方程和分離變量

ref 積分 sub 名稱 答案 曲線 技術 斜率 理學 常微分方程 　　含有未知函數的導數，如 　　的方程是微分方程。 一般的，凡是表示未知函數、未知函數的導數與自變量之間的關系的方程，叫做微分方程。未知函數是一元函數的，叫常微分方程；未知函數是多元函數的叫做偏微分方

數學筆記12——常微分方程和分離變數

 常微分方程　　含有未知函式的導數，如　　的方程是微分方程。 一般的，凡是表示未知函式、未知函式的導數與自變數之間的關係的方程，叫做微分方程。未知函式是一元函式的，叫常微分方程；未知函式是多元函式的叫做

常微分方程1：與方程聯系的相流

方法 option 一點 display 是否 http tle 位置 title 1.1 向量場 中一開集上的向量場指的是上的一個向量值函數: 1.2 常微分方程 上的常微分方程指的是形如 : 的方程，其中是定義在 上的向量場.若

2017-2018-1(現代偏微分方程導論 36)

導論 數學 bsp size 研究生 ont 方程 span pan 2017-2018-1(現代偏微分方程導論 36) 現代偏微分方程 (16級數學研究生) [9-11 周一(9,10,11) 7-305,周二(9-11) 7-305] 廖強2017-2018-

2017-2018-2偏微分方程復習題解析8

-s roo CA BE 題解 posit $$ ads any Problem: (1) Narrate the resonance theorem. (2) Let $X$ be a Banach space, and denote by $C_w([0,T];X)$

2017-2018-2偏微分方程復習題解析9

fin 題解 bbr style dial 習題 -s spa pro Problem: Let $K,f,g$ be in $\calD(\bbR^d)$, and $K$ is radial (for definition, see Problem 2). Show t

偏微分方程數值解---學習總結

學習 sch 方程 iii omega sub 雙線 線性空間 分布函數 偏微分方程數值解---學習總結 1.知識回顧 （註:\(\mit V\)是線性空間） 內積 $(\cdot ,\cdot):\mit V \times \mit V \longrightarrow

偏微分方程數值解---學習總結(2)

偏微分方程數值解---學習總結(2) 關於 \(Sobolve\) 空間的幾個重要定理 跡定理 : \(\Omega\) 是 \(\mathbb{R}^d\) 的一個有界開子集，具有 李普希茨連續邊界 \(\partial\,\Omega\), \(s>\frac{1}{2}\), 則 \[ \be

偏微分方程：計算基本理論

1. 偏微分方程 　　偏微分方程（Partial Differential Equation，簡寫為PDE）是未知量包含多個獨立變數、方程包含偏微分運算的一類微分方程。 　　在物理模型中，最常見的情況是：需要求解的未知量含有時間變數(t)和空間變數（視維數變化）。最簡單的偏微分方程包括二維穩定問題（只和空

tensorflow官方文件中文版-偏微分方程-可執行版

#python3.6 import tensorflow as tf import numpy as np import PIL.Imagefrom io import BytesIO from IPython.display import clear_output, Image, disp

偏微分方程數值解

1.求解拉普拉斯方程的狄利克雷法 求解在區域R = {(x,y): 0≤x≤a, 0≤y≤b}內的 uxx(x,y) + uyy(x,y) = 0 的近似解，而且滿足條件 u(x,0) = f1(x),  u(x,b) = f2(x), 其中0≤x≤a 且 u(0,y

線性代數之——微分方程和 exp(At)

本節的核心是將常係數微分方程轉化為線性代數問題。 d u

【數值計算】數值解析--二階偏微分方程的3種基本形

2階偏微分方程的3種基本型別 2階偏微分方程的3中基本型別有:橢圓型，雙曲線型，拋物線型。 首先，關於的2階偏微分方程的一般形式為， 這裡的是與相關的函式。 根據與2階偏微分項相關的係數，

常系數線性差分方程的求解

ges ima baidu cnblogs blog common targe 技術 求解 地址：https://wenku.baidu.com/view/f191d2ea102de2bd960588ae.html 常系數線性差分方程的求解

偏導數與全導數的關係 以及 偏微分與全微分的關係

1.偏導數 代數意義  偏導數是對一個變數求導,另一個變數當做數 對x求偏導的話y就看作一個數,描述的是x方向上的變化率 對y求偏導的話x就看作一個數,描述的是y方向上的變化率 幾何意義 對x求偏導是曲面z=f(x,y)在x方向上的切線 對y求偏導是曲面z=f(x,y)在x方向

偏導數，全導數，方向導數，偏微分，全微分，梯度

學習到機器學習線性迴歸和邏輯迴歸時遇到了梯度下降演算法，然後順著扯出了一堆高數的相關概念理論：導數、偏導數、全微分、方向導數、梯度，重新回顧它們之間的一些關係，從網上和教材中摘錄相關知識點。 這段是我的簡單總結，如果看不懂沒關係，先看下面的定義 通過函式的極限定義出導數

牛頓法和割線法方程求根（C語言）

1 . 實驗目的 (1) 通過對二分法與牛頓迭代法作程式設計練習與上機運算，進一步體會二分法與牛頓迭代法的不同特點。 (2) 編寫割線迭代法的程式，求非線性方程的解，並與牛頓迭代法作比較。

S域到Z域變換和差分方程

1.s域的傳遞函式 G(s) = 2 / (1500s + 1) * exp(-100s) matlab 裡面的命令是 sys = tf(2,[1500,1],'inputdelay',100) 得到           &nbs

Extracting Lines Using Differential Geometry and Gaussian Smooth--Carsten Steger 使用微分幾何和高斯平滑進行邊緣提取

在csdn中編輯公式參考： http://blog.csdn.net/gateway6143/article/details/23134225 論文思路 一、 對直線（一維曲線的檢測） 1. 真實影象常常包含噪聲，對影象進行平滑去噪（高斯平滑）：