Logistic迴歸cost函式的推導過程。演算法求解使用如下的cost函式形式：

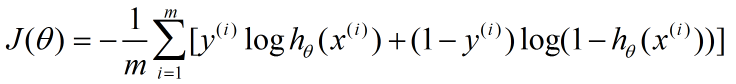
梯度下降演算法

對於一個函式，我們要找它的最小值，有多種演算法，這裡我們選擇比較容易用程式碼實現和符合機器學習步驟的梯度下降演算法。

先來看看梯度下降演算法中，自變數的迭代過程。表示如下

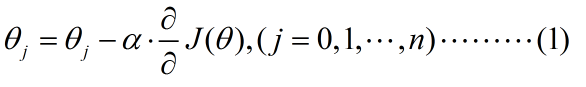
可以看到，這是一個θ值不斷迭代的過程，其中α是學習速率，就是θ的移動“步幅”，後面的偏導數數就是梯度，可以理解為cost函式在θ當前位置，對於j位置特徵的下降速度。

　　對於二維空間，梯度可以理解為函式影象的切線斜率。即：特徵是一維的

　　對於多維特徵，cost函式的影象就應該是這樣的，下面舉個例子：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　圖1 cost函式舉例

　　這是一個二維特徵的cost函式的影象，這個時候，梯度有無限多個，我們不能只說cost函式的梯度，應該說，cost函式在某個方向上的梯度。例如，cost函式在θ0方向上，在(θ0=m,θ1=n)上的梯度就是cost函式與θ1=n這個平面的交線在（m,n）處的斜率。

　　上面的描述比較抽象，簡單說來，假設影象就是一個小山坡（有點像吧），你站在影象的（m,n）點處，朝θ0的方向看過去，看到的“山坡”的“坡度”就是上面所說的梯度了。

　　這個迭代過程，用形象化的語言描述，就是：

　　　　我站在山坡上，找到一個初始點θ

　　然而，這樣的“盆地”可能有多個，我們不同的走法，可能會走到不同的山底，如圖：

　　　　　　　　　　　　　　　　　　　　　　　　　　　圖2 多“山谷”cost函式

　　這裡的兩條路線分別走向不同的山谷，這就說明：梯度下降演算法只能求出一個區域性最小值，不一定是全域性最小值，但這不影響它是一個好的方法。

這樣，θ的迭代過程就講清楚了。接下來說一下迭代的終止條件。

　　迭代肯定不是無限下去的，我們不妨想一下：當我們走到了山谷，再想往某個方向走的時候，發現都不能再往下走了，那麼我們的旅行就終止了。

　　同樣，當θ迭代了n次後（就如圖2的黑線一樣），發現接下來走α這麼長的路，下降的高度很小很小（臨界值），或者不再下降，甚至反而往上走了，所以我們的迭代終止條件就是cost函式的減少值小於某個值。

　　我們再來回顧一下迭代公式（1）：其中α是經驗設定，稱之為learning rate，初始值也是隨機選定，那麼後面的那個梯度呢？

　　梯度就是cost函式對於特徵向量某一維的偏導數。我們來看看這個怎麼推導和簡化。

　　【梯度的求解】

　　推導過程：

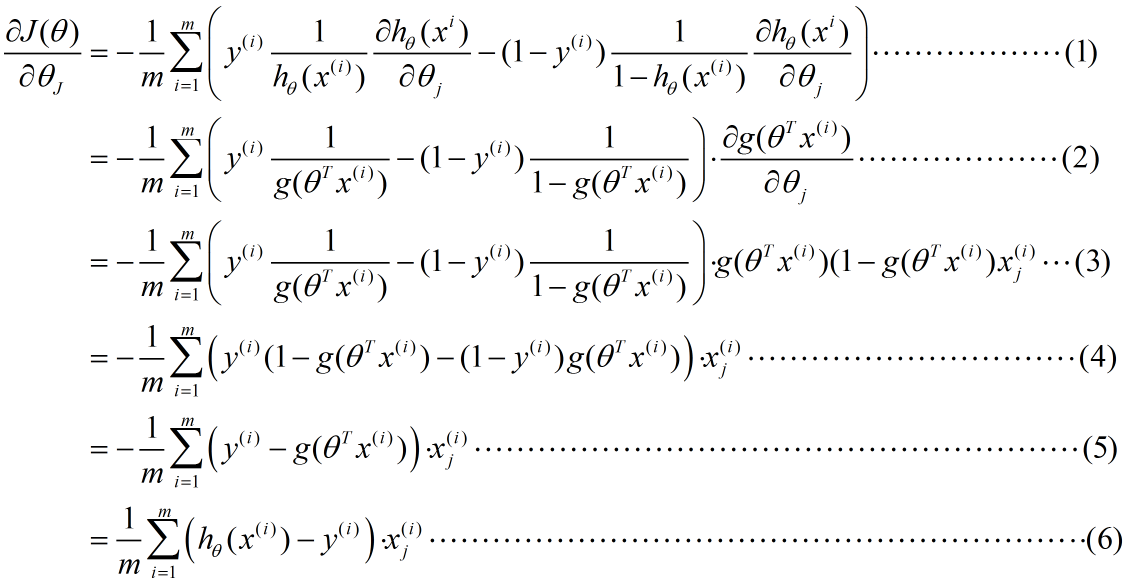
　　解釋一下推導流程，便於理解。

　　(1)--->(2)：使用sigmoid函式的形式g(z)替換hθ(x)、提出公因子，放在式子尾

　　(2)--->(3)：這一步具體推導如下（使用了複合函式的求導公式）

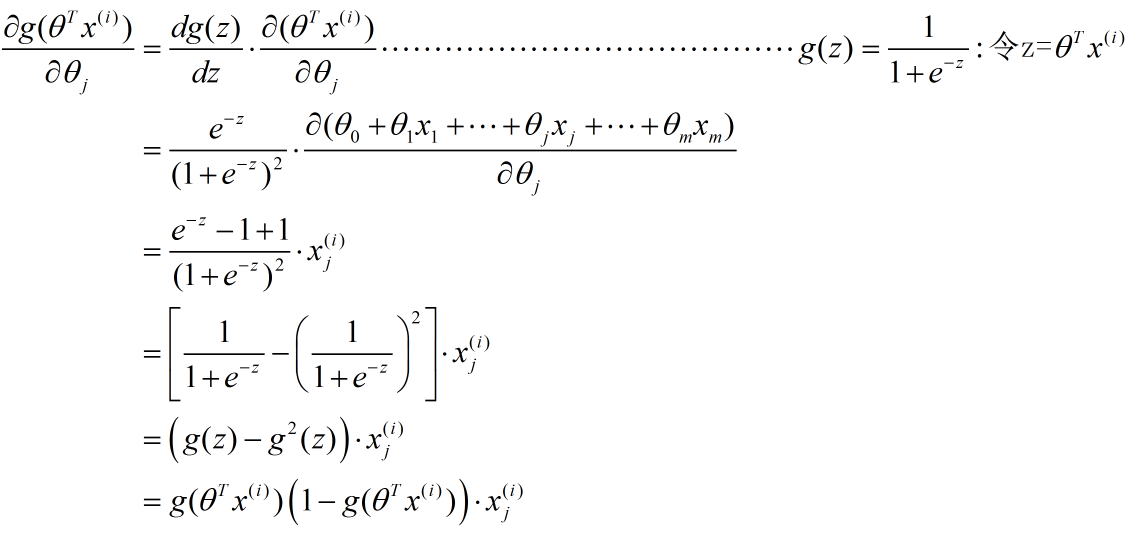
　　後面的幾步較為簡單，就不另作說明了。

　　【演算法執行】

　　到了這裡，我們推出了迭代公式的最終形式：

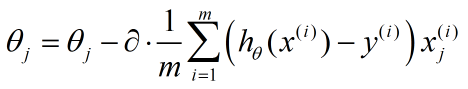
　　更一般的形式就是把j去掉，表示對特徵的每一維都如此迭代

　　注意，在迭代過程中，θ的所有特徵是同步更新的，所以根據給定的資料集，就能使用梯度下降演算法來求解θ了，迭代終止條件即是將當前θ帶入cost函式，求出代價值，與上一個代價值相減，結果小於閾值，立即停止迭代。