【數學基礎】最小二乘法
前言
當我們有組資料,希望能夠用一個函式來擬合這組資料的分佈情況時,首先想到的就是最小二乘法。最小二乘法是線性迴歸中最基礎也是最常用模型,它也可以用來擬合高次多項式。
什麼是最小二乘法
那麼,什麼是最小二乘法呢?將我們手中已有的資料表示成一個集合,(為了簡化模型,暫且只考慮輸入屬性只有一個的情況)
首先假設最終得到的線性模型為;
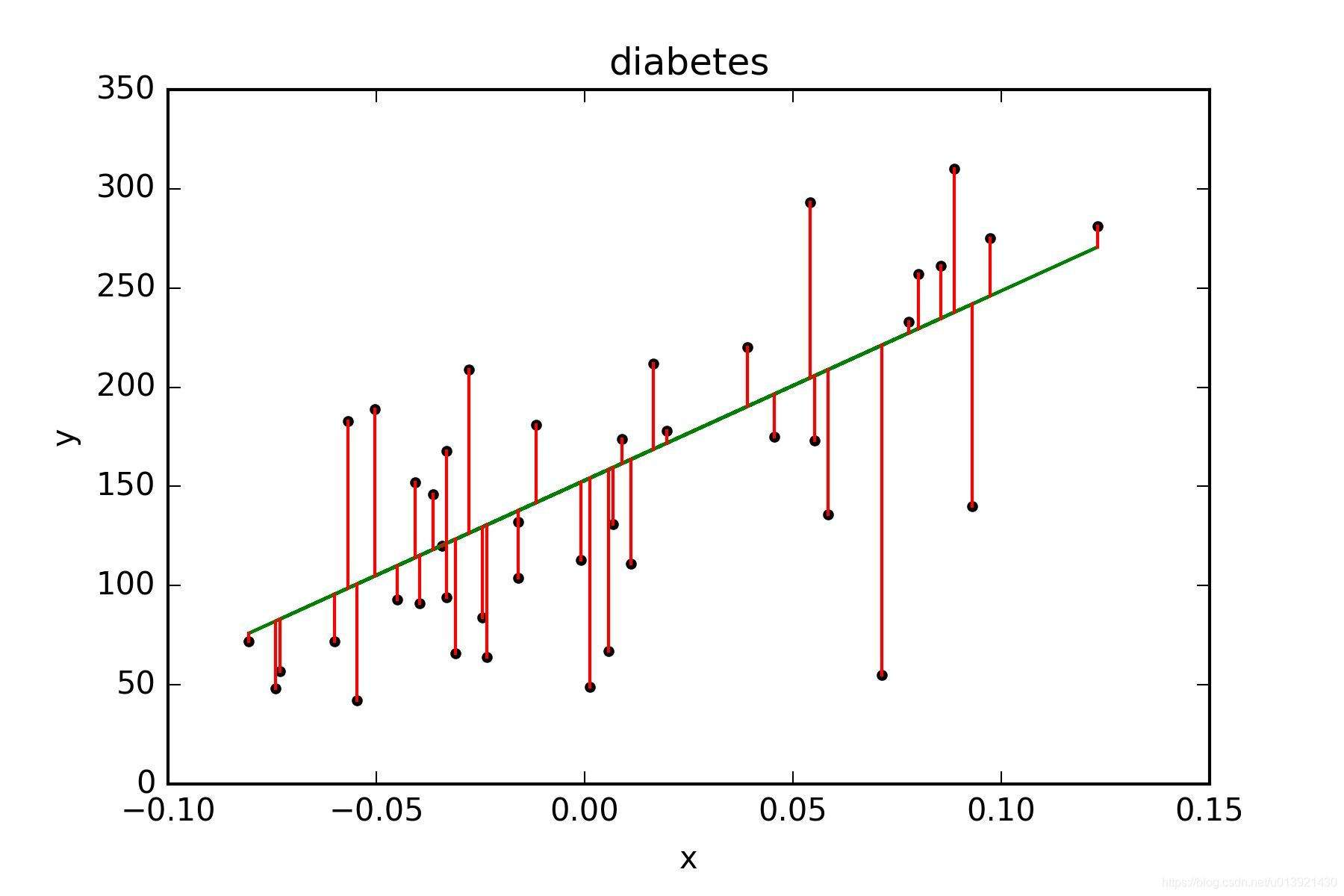
如上圖所示,綠色的線條為所求的迴歸模型,黑色點為實際樣本輸入資料,紅色線段為實際值與模型預測值之間的歐氏距離,用以下公式表示;
為了讓最終所求的模型儘量準確地表現資料分佈規律,我們需要讓的和儘可能的小,所以在的和取最小值時取得;
但是上述式子中的絕對值是不可導的,求解困難。因此採用均方誤差來代替絕對值。
這種基於均方誤差來進行模型求解的方法就叫最小二乘法,也叫最小平方法。
引數推導
首先還是來看上面提到的最簡單的情況。令;
前言
當我們有NNN組資料,希望能夠用一個函式來擬合這組資料的分佈情況時,首先想到的就是最小二乘法。最小二乘法是線性迴歸中最基礎也是最常用模型,它也可以用來擬合高次多項式。
什麼是最小二乘法
那麼,什麼是最小二乘法呢?將我們手中已有的資料表示成一個集
【機器學習】最小二乘法支援向量機LSSVM的數學原理與Python實現
一、LSSVM數學原理
1. 感知機
2. SVM
3. LSSVM
4. LSSVM與SVM的區別
二、LSSVM的py
回顧
迴歸分析之線性迴歸 中我們得到了線性迴歸的損失函式為:
J
(
θ
數學基礎
1.轉置矩陣
定義: 將矩陣A同序數的行換成列成為轉置矩陣ATA^TAT,舉例:
A=(1203−11)A=\begin{pmatrix}
1 & 2 & 0 \\
3 & -1 &
【參考資料】
【1】《概率論與數理統計》
【2】 http://scikit-learn.org /stable/auto_examples/ linear_model/ plot_ols.html # sphx-glr-auto-examples-
【機器學習】用QR分解求最小二乘法的最優閉式解
寫在前面
QR分解
定義
QR的求解
線性迴歸模型
用QR分解求解最優閉式解
矩陣的條
最小二乘法(又稱***最小平方法***)是一種數學優化技術。它通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料,並使得這些求得的資料與實際資料之間誤差的平方和為最小。最小二乘法還可用於曲線擬合。其他一些優化問題也可通過最小化
線性迴歸
線性迴歸(Linear Regreesion)就是對一些點組成的樣本進行線性擬合,得到一個最佳的擬合直線。
最小二乘法
線性迴歸的一種常用方法是最小二乘法,它通過最小化誤差的平方和尋找資料的最佳函式匹配。
代數推導
假設擬合函式為 y Ordinary Least Square 最小二乘法
提到最小二乘法要先提到擬合,擬合Fitting是數值分析的基礎工具之一,在二維平面上分為直線擬合和曲線擬合,直線擬合找到一條直線儘可能穿過所有的點,注意這裡是儘可能,因為只要超過2個點,就有可能發生直線不能精確穿過所有點的情況,這時確定直線的原則有很多 方法 最小值 幾何 adc 直線方程 dstat 技術分享 ecb image Ordinary Least Square 最小二乘法
提到最小二乘法要先提到擬合,擬合Fitting是數值分析的基礎工具之一,在二維平面上分為直線擬合和曲線擬合,直線擬合找到一條直線盡可能穿過 基礎 int 復雜度 amp pan -1 log 分治 質數 費馬小定理:當p是一個質數時,且a和p互質,有ap-1=1(mod p) (歐拉定理的一種特殊情況)
歐拉定理:如果a和n互質,那麽aφ(n)=1(mod n)
對於任意a,b,n就有 ab=
網上看到的最小二乘法都是互相抄來抄去,一錯一大片,連標點符號都錯的一樣,其實整個推導過程並不是很難的一件事,只需要簡單的一步步按照最小化損失函式就可以得到,對於新手來說這些答案誤導性比較強。最終我們需要得到的線性方程為
y^=β0+β1x^
\hat{y} =
1.LS演算法說明
LS演算法是一種數學優化技術,也是一種機器學習常用演算法。他通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便的求得未知的資料(1),並使得這些求得的資料與實際資料之間誤差的平方和最小。除此之外最小二乘法還可用於曲線擬合(2),其他一些優化問題(
泛化與過擬合
olympval.m
Load the Olympic data and extract the training and validation data
load data/olympics
x = male100(:,1);
t
費馬小定理:當p是一個質數時,且a和p互質,有ap-1=1(mod p) (尤拉定理的一種特殊情況)
尤拉定理:如果a和n互質,那麼aφ(n)=1(mod n)
對於任意a,b,n就有 ab=aφ(n)+b mod φ(n)(mod n) 處理b數值較大的情況 ,採 1.r(A)=未知數個數n(約束較強)
1.1.A是方陣
由克萊姆法則可知:
如果A是n*n的方陣而且r(A)=n,那麼該方程組有唯一的零解。 1.2.A不是方陣,A是m×n的(m>n)
由另一個定理:齊次線性方程解空間維數 = n - r 一次函數 python 散點圖 博客 如何 這裏只是介紹下R語言中如何使用最小二乘法解決一次函數的線性回歸問題。 代碼如下:(數據同上一篇博客)(是不是很簡單????)> x<-c(6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1 python 技術 如何 模型 平面 之所以說”使用”而不是”實現”,是因為python的相關類庫已經幫我們實現了具體算法,而我們只要學會使用就可以了。隨著對技術的逐漸掌握及積累,當類庫中的算法已經無法滿足自身需求的時候,我們也可以嘗試通過自己的方式實現各種算法。 言 red num class cat blank height mar 感覺 時間 一、引言
這段時間學習《機器學習》,學到第5章的“Logistic回歸”,感覺相當吃力。追本溯源,從“Logistic回歸”到“線性回歸”,再到“最小二乘法”。最終定格到了《高等數學》(第六版 得出 ack 提高 kernel sys 風險 重要 ref height
在機器學習或者是模式識別其中有一種重要的分類器叫做:SVM 。這個被廣泛的應用於各個領域。可是其計算的復雜度以及訓練的速度是制約其在實時的計算機應用的主要原因。因此也非常非常多的算法
是關於與的二次函式,只會有一個極值點。而很明顯,讓取極大值的出現在空間中無限遠處的,是不存在的。所以當讓取得極值時,取得極小值,分別對、求偏導。
令;
可得;
由於,
相關推薦
【數學基礎】最小二乘法
【機器學習】最小二乘法支援向量機LSSVM的數學原理與Python實現
【機器學習】最小二乘法求解線性迴歸引數
【機器學習筆記02】最小二乘法(多元線性迴歸模型)
【機器學習筆記01】最小二乘法(一元線性迴歸模型)
【機器學習】用QR分解求最小二乘法的最優閉式解
最小二乘法【一】
【機器學習筆記】線性迴歸之最小二乘法
【原創】演算法分享(7)最小二乘法
【原創】算法分享(7)最小二乘法
【數學基礎】【歐拉定理模板】【費馬小定理】
最小二乘法的數學
python3__機器學習__神經網路基礎演算法__最小二乘法(LS演算法)
ML基礎教程:泛化與過擬合、正規化最小二乘法
【數學基礎】【尤拉定理模板】【費馬小定理】
[數學]齊次線性方程組的解、SVD、最小二乘法
R語言中如何使用最小二乘法
Python中如何使用最小二乘法
機器學習-最小二乘法
Regularized least-squares classification(正則化最小二乘法分類器)取代SVM
