二叉搜尋樹的原始碼分析學習 筆記(完整版 包含原始碼和visio下載)
阿新 • • 發佈:2019-01-02
- 上篇部落格介紹了二叉搜尋樹的建立,插入結點,遍歷結點,查詢結點,最大結點,最小結點,後繼結點。
- 那麼這篇部落格要重點介紹二叉搜尋樹的節點刪除函式,一些資料結構的書籍裡介紹的二叉搜尋樹刪除節點的方法說的非常之模糊,能把一個老司機說成萌新。
二叉搜尋樹刪除結點
-
如果node z存一個孩子或者沒有孩子,那麼他的孩子結點頂替z結點位置,然後把node z刪除free掉。下圖就是一個孩子或者沒有孩子的操作。
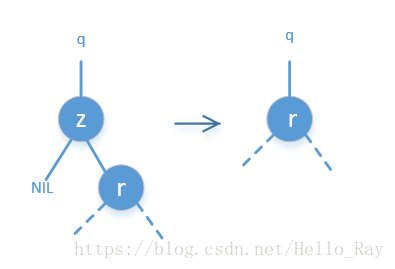
只有右孩子的情況
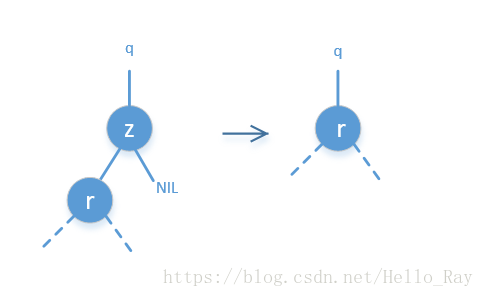
只有左孩子的情況
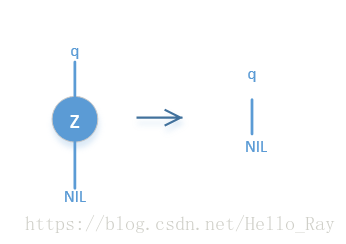
沒有孩子的情況
根據上面的圖片顯示,從而想到一個問題:在node z 只有一個孩子結點或者沒有孩子結點情況,為什麼孩子結點直接頂替他的位置就是刪除結點的操作。
這個問題是這樣解決的
- 只有右孩子情況:根據結點的排序z r,如果刪除node z結點結點,從這裡排列的情況來看,r就是他後面的一個結點,或者是他鄰居的結點,所以r可以直接替換。
- 只有左孩子情況:同理排列r z。注意node z的右子樹為空,所以到z就結束了,z為最大的結點,所以刪除z,在樹裡r結點直接頂上去。
- 沒有孩子的情況:無需排列了,z結點是光棍,啥都沒了。熟話說一人吃飽全家不餓,無憂無慮,所以這種情況刪除z結點最快
node z只有一個結點或者沒有結點的程式碼執行流程是程式碼中的註釋要仔細看
//node z是要刪除的結點,賦值給y
y=z;
//x指向的是 y 的孩子結點,等同於上圖的 r 結點
if 結論: 只有一個或者沒有孩子的node z是很好處理,只要讓他的孩子頂替上去就行了
-
如果node z存在左孩子和右孩子,刪除node z主要分為下面的幾個步驟進行
- 找到node z後繼結點,後繼結點的地址賦值給y,
- x作為y結點的孩子結點,然後像上面的x頂替y的方法一樣,讓x頂替y,
- 然後把y的值賦給z就行了,就相當於把z給刪掉了。
下面有兩種情況我們看一下
-
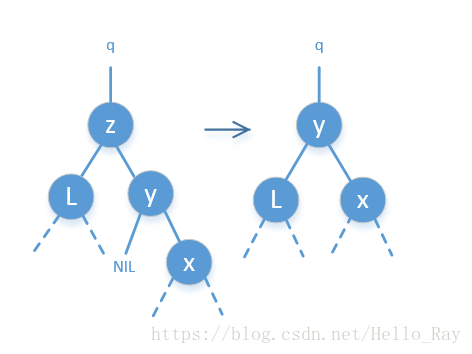
z的後繼結點y,y也是z的右孩子。如下圖
-
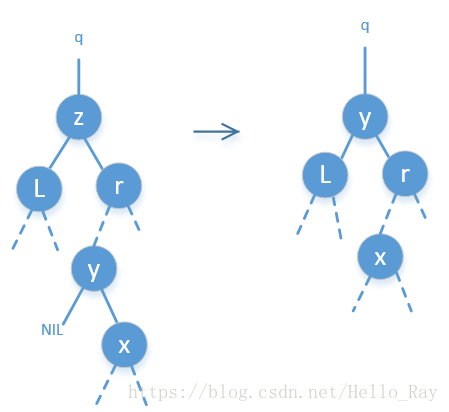
z的後繼結點y,y在z的右子樹中,且y不是z的右孩子。這種情況如下圖
node z存在兩個結點的程式碼執行流程是
注意:程式碼流程中存在一些函式,在上篇部落格中,而且程式碼中的註釋要仔細看
//node z是要刪除的結點,找到他的後繼結點賦值給y
y=bstree_successor(z);
//x指向的是 y 的孩子結點
if(y->left != NULL)
x = y->left;
else
x = y->right;
//調整x結點指向父親結點的位置,這個時候就相當於x頂替上去,準備把y換下。
if(x != NULL)
x->parent=y->parent;
/*
x的父親結點已經指向了y的父親結點
想要頂替別人還要知道那個人(node y)在他的家庭裡中什麼地位
這一步就是要清楚知道y是他父親的左兒子還是右兒子,還是整顆樹的根節點。
*/
if(y->parent == NULL)
tree = x;
else if(y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
/*
我們已經知道,y已經被頂替了。但是y被頂替了,而z逍遙自在沒人慣了違背初衷了。
不要著急,只要把y的值給z就行了。
不信的話,看看上圖就知道了,是不是感覺到很巧妙很神奇。↖(^ω^)↗
*/
if(y != z)
z->key = y->key;
/*
x頂替y的結束了: 認了y的爸爸當爸爸,然後擁有和y一樣在家庭的地位,此時y就多餘了,
那麼就要讓y下臺
*/
free(y);
下一步就是我要把上面的兩個方法合併到一起
注意: z是傳入刪除結點的地址
node * bstree_delete(bst_tree tree, node * z)
{
node * x = NULL;//x充當 要刪除結點z的左結點或者右結點或者空結點,
node * y = NULL;//y充當 要刪除結點z
/**
* 如果z結點存在左右結點,那麼就查詢他的後繼結點,他的後繼結點當作y
* 如果存在一個結點或者不存在結點,那麼本身結點就當作y
*/
if((z->left == NULL) || (z->right == NULL))
y=z; //存在一個結點或者沒有結點情況
else
y=bstree_successor(z); //存在兩個結點情況
//x指向y的左孩子或者右孩子
if(y->left != NULL)
x = y->left;
else
x = y->right;
//調整x父親結點的位置。使其x的父親結點指向y的父親結點
if(x != NULL)
x->parent = y->parent;
//調整y父節點指向x
if(y->parent == NULL)
tree = x;
else if(y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
//y的值賦給z就相當於刪除了z,這種做法很巧妙,可以結合上圖檢視。
if(y != z)
z->key = y->key;
free(y);
return NULL;
}
下面這一個判斷程式碼,本來非常糾結,為什麼要進行這種的驗證呢。
目前的想法是:根據上面圖片所展示的情況,如果y->left != NULL成立,那麼假設以y為根節點(y結點開始,下面所有的孩子結點),y的value是最大的。
如果y不是最大結點,都是走下面那個程式碼 x=y->right
//x指向的是 y 的孩子結點
if(y->left != NULL)
x = y->left;
else
x = y->right;
參考文獻 Introduction to Algorithms [MIT press]